Problem - C - Codeforces

翻译：

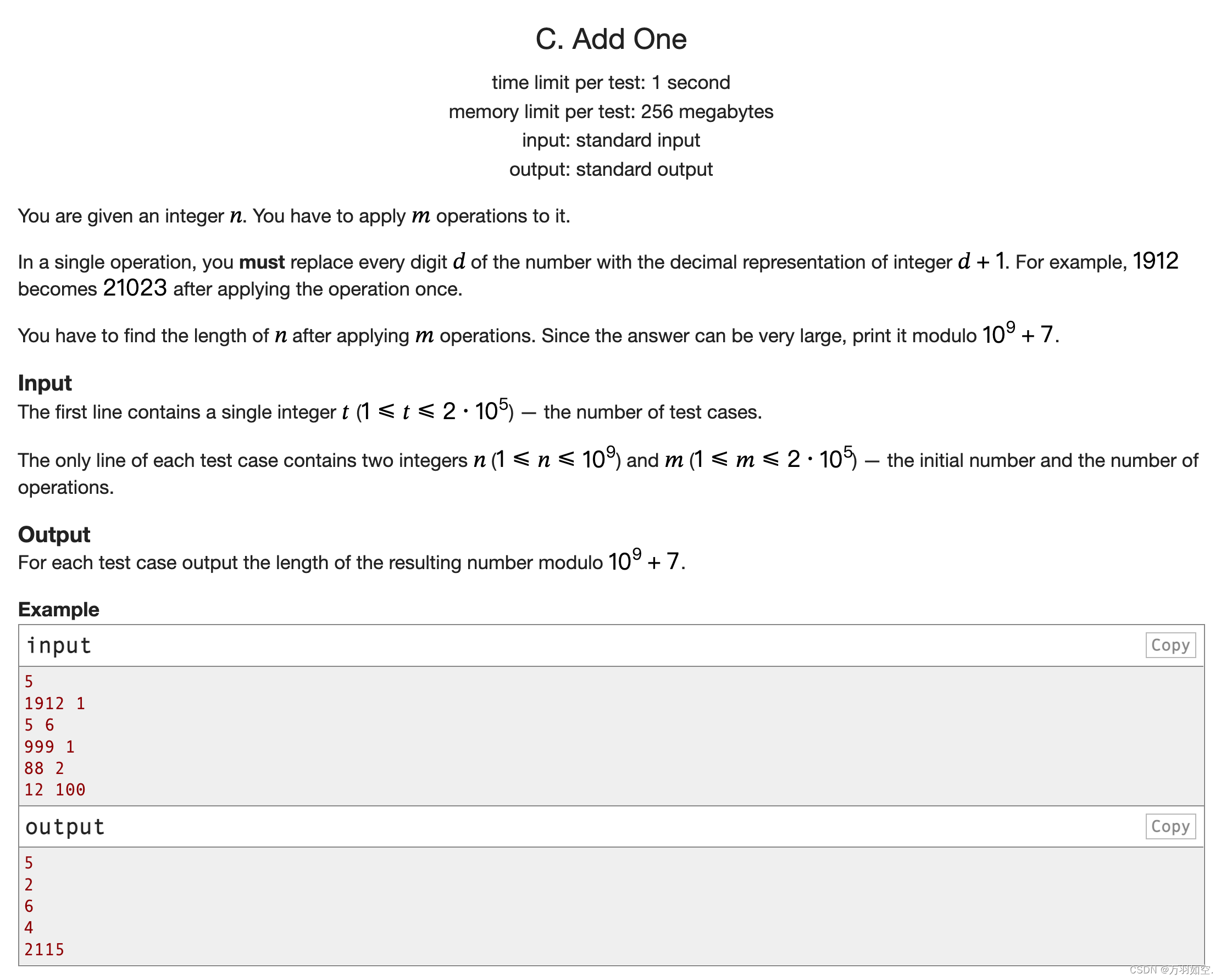
给你一个整数𝑛。您必须对其应用𝑚操作。

在单个操作中，必须将该数字的每个数字𝑑替换为整数𝑑+1的十进制表示形式。例如，在应用一次操作后，1912变成21023。

在应用𝑚操作后，必须找到𝑛的长度。因为答案可以很大，对109+7取模打印。

输入
第一行包含一个整数𝑡(1≤𝑡≤2⋅105)——测试用例的数量。

每个测试用例的唯一一行包含两个整数𝑛(1≤𝑛≤109)和𝑚(1≤𝑚≤2⋅105)——初始数和操作数。

输出
对于每个测试用例，输出结果数对109+7模的长度。

例子
inputCopy
5
1912年1
5个6
999年1
88 2
100年12
outputCopy
5
2
6
4
2115
请注意
对于第一个测试，1912在1个长度为5的操作后变成21023。

对于第二个测试，5在6次操作后变成21，长度为2。

对于第三个测试，999在经过1个长度为6的操作后变成101010。

对于第四个测试，88经过两次运算后变成1010，长度为4。

思路：

就是操作m次，然后每次给每个数字加上1，数据范围挺小，开了个数组直接去暴力想着也就m*10的复杂度，忘了还有个T，这道题没有给总数的范围限制，所以无脑只会T。后来仔细想了一下，只有9+1才会变成两位数字10，0 1 2 3 4 5 6 7 8这些数字变化不会增加位数，只有达到9+1，才会对答案有贡献，所以我们直接对9预处理出来2e5次操作的情况，其余数字就是减去其到9的操作，然后再统计，这样的话只需要预处理一个数字即可。

之后我们统计给的数字个数，然后直接求和即可。

嗲吗：

#include <iostream>
#include <algorithm>
#include <string.h>
#include <string>
#include <math.h>
#include <stdio.h>
#include<vector>
#include<queue>
#include<map>
#include<set>
#include<tuple>
#include<numeric>
#include<stack>
using namespace::std;
typedef long long  ll;
int n,t;
inline __int128 read(){
    __int128 x = 0, f = 1;
    char ch = getchar();
    while(ch < '0' || ch > '9'){
        if(ch == '-')
            f = -1;
        ch = getchar();
    }
    while(ch >= '0' && ch <= '9'){
        x = x * 10 + ch - '0';
        ch = getchar();
    }
    return x * f;
}
inline void print(__int128 x){
    if(x < 0){
        putchar('-');
        x = -x;
    }
    if(x > 9)
        print(x / 10);
    putchar(x % 10 + '0');
}
const ll N=1e9+7;
ll an,m;
ll ff[10];
ll yuc[200005];
void solv(){
    for (int i =0; i<10; i++) {
        ff[i]=0;
    }
    cin>>an>>m;
    while (an>0) {
        ff[an%10]++;
        an/=10;
    }
    
//    for (int i =0; i<m; i++) {
//        for (int  j= 9; j>=1; j--) {
//            swap(ff[j],ff[j-1]);
//            ff[j]%=N;
//        }
//        ff[1]=(ff[1]+ff[0])%N;
//        ff[0]%=N;
//    }
    ll ans=0;
    for (int i =0; i<=9; i++) {
        if (9-i>=m) {
            ans=(ans+ff[i])%N;
        }
        else{
            ans=(ans+yuc[m-(9-i)]*ff[i])%N;
        }
    }
    
    printf("%lld\n",ans);
}
int main(){
    ios::sync_with_stdio(false);
    cin.tie(); cout.tie();
    yuc[0]=1;
    ff[9]=1;
    for (int i =1; i<200001; i++) {
        for (int  j= 9; j>=1; j--) {
            swap(ff[j],ff[j-1]);
            ff[j]%=N;
            yuc[i]=(yuc[i]+ff[j])%N;
        }
        ff[1]=(ff[1]+ff[0])%N;
        ff[0]%=N;
        yuc[i]=(yuc[i]+ff[0]*2)%N;
    }
//    for (int i =0; i<=100; i++) {
//        printf("i::%d %lld\n",i,yuc[i]);
//    }
    cin>>t;
    while (t--) {
        solv();
    }
    return 0;
}