网格的谱分解即网格的频率分解，我们学过信号的傅里叶变换，将信号从空域变换到频域。二维图像由离散傅里叶变换DFT(Discrete Fourier Transform)。在图信号领域，也有图的傅里叶变换GFT(Graph Fourier Transform)，网格可以看作是图，因此网格的谱分解，就是进行图傅里叶变换。
在这里插入图片描述

网格谱分解

GFT图傅里叶变换

先构建图的拉普拉斯矩阵，拉普拉斯矩阵=度矩阵-邻接矩阵
计算拉普拉斯矩阵的特征值和特征向量：对构建的拉普拉斯矩阵进行特征值分解，得到其特征值和对应的特征向量。特征值表示了网格的频谱信息，而特征向量则表示了网格不同的频谱分量。
然后将图的拉普拉斯矩阵可以表示程基向量的线性组合，其系数就代表了不同频率分量的强度。
在特征值中，较大的特征值对应的频谱分量通常包含了网格中的高频信息，而较小的特征值对应的频谱分量则表示了网格中的低频信息。因此，可以通过特征值的大小来判定高频信息。

图的拉普拉斯矩阵

拉普拉斯矩阵=度矩阵-邻接矩阵

为什么这个矩阵叫拉普拉斯矩阵呢？依我有限的理解，可以联系网格顶点的拉普拉斯坐标。
假设图有n个顶点，则图的拉普拉斯矩阵 $L^{n\times n}$ ，将图的顶点坐标也表示为矩阵为 $V^{n\times 3}$ , 将拉普拉斯矩阵左乘顶点矩阵，即 $\times V$ ，得到的是图的顶点的拉普拉斯坐标矩阵 $Lv^{n\times 3}$

举个栗子

拉普拉斯矩阵=度矩阵-邻接矩阵

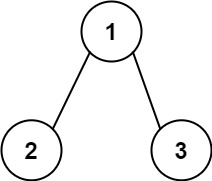
考虑一个简单的二维网格，由4个顶点和4条边组成，如下所示：

   1 -- 2
   |    |
   3 -- 4

我们可以使用邻接矩阵和度矩阵来构建拉普拉斯矩阵。

邻接矩阵：邻接矩阵表示了顶点之间的连接关系。在这个例子中，邻接矩阵为：

   [[0, 1, 0, 1],
    [1, 0, 1, 0],
    [0, 1, 0, 1],
    [1, 0, 1, 0]]

度矩阵：度矩阵表示了每个顶点的度数（即与之相连的边的数量）。在这个例子中，度矩阵为：

   [[2, 0, 0, 0],
    [0, 2, 0, 0],
    [0, 0, 2, 0],
    [0, 0, 0, 2]]

拉普拉斯矩阵：通过将度矩阵减去邻接矩阵，我们可以得到拉普拉斯矩阵。在这个例子中，拉普拉斯矩阵为：

   [[2, -1, 0, -1],
    [-1, 2, -1, 0],
    [0, -1, 2, -1],
    [-1, 0, -1, 2]]

这个拉普拉斯矩阵描述了网格中顶点之间的连接关系和边界条件。通过对该矩阵进行特征值分解，可以进行网格的谱分解和频谱分析。
对于给定的拉普拉斯矩阵：

$\begin{bmatrix} 2 & -1 & 0 & -1 \\ -1 & 2 & -1 & 0 \\ 0 & -1 & 2 & -1 \\ -1 & 0 & -1 & 2 \\ \end{bmatrix}$

进行特征值分解

使用适当的数值计算库或线性代数软件进行特征值分解。这可以通过调用相应的函数或方法来完成。

特征值分解的结果可以表示为：
$Q\Lambda Q^{-1}$

其中， $Q$ 是特征向量矩阵， $\Lambda$ 是特征值对角矩阵。

得到结果如下：

特征值（Eigenvalues）：
$\lambda_1 = 0$ ， $\lambda_2 = 1$ ， $\lambda_3 = 3$ ， $\lambda_4 = 4$

特征向量（Eigenvectors）：
$v_1 = \begin{bmatrix} 1 \\ 1 \\ 1 \\ 1 \end{bmatrix}$
$v_2 = \begin{bmatrix} -1 \\ 1 \\ -1 \\ 1 \end{bmatrix}$
$v_3 = \begin{bmatrix} 1 \\ -1 \\ -1 \\ 1 \end{bmatrix}$
$v_4 = \begin{bmatrix} -1 \\ -1 \\ 1 \\ 1 \end{bmatrix}$

请注意，特征值的顺序是按照从小到大排列的。特征向量对应于特征值的顺序，即 $v_1$ 对应于 $\lambda_1$ ， $v_2$ 对应于 $\lambda_2$ ，依此类推。

特征值分解提供了关于矩阵的结构和性质的重要信息。在这个例子中，特征值分解揭示了该网格的特征模式和频率，其中特征值 0 对应于一个常数模式，特征值 1 对应于一个线性模式，特征值 3 和 4 对应于更高频率的模式。特征向量表示了每个特征模式的空间形状。

应用

网格压缩

Spectral Compression of Mesh Geometry

文章概述：
这篇文章主要介绍了一种称为"网格几何谱压缩"的技术，用于对网格几何数据进行压缩。该方法利用了网格的谱性质，并通过保留关键频率分量来实现高效的压缩。作者通过实验证明了该方法在减小网格数据尺寸的同时，能够保持较高的几何质量和视觉效果。

技术要点：

网格谱性质的利用： 该方法利用了网格的谱性质，即网格的特征向量和特征值之间的关系。通过对网格进行谱分解，可以得到一组特征向量和对应的特征值，这些特征向量表示了网格的几何形状。基于这些特征向量，可以对网格进行重建或者压缩。
关键频率分量的保留： 为了实现高效的压缩，该方法选择保留网格特征向量中的关键频率分量，即对应于较大特征值的特征向量。这些关键频率分量包含了网格的主要几何信息，而忽略较小特征值对应的特征向量可以有效减小数据尺寸。
压缩算法： 文章提出了一种基于关键频率分量的压缩算法。该算法首先对网格进行谱分解，然后根据预设的压缩比例选择要保留的特征向量数量。通过仅保留关键频率分量并丢弃其他分量，可以大幅减小数据尺寸。最后，利用保留的特征向量重建原始网格。

相比以前方法的改进：
相较于以前的方法，这篇文章提出的网格几何谱压缩方法具有以下改进：

高效性： 该方法利用了网格的谱性质，通过保留关键频率分量实现了高效的压缩。相比于传统的方法，该方法可以在减小数据尺寸的同时保持较高的几何质量和视觉效果。
几何质量的保持： 该方法在压缩过程中，选择保留关键频率分量，这些分量包含了网格的主要几何信息。因此，通过该方法压缩后的网格能够保持较高的几何质量，避免了传统压缩方法可能引入的形变或失真。

文章的不足：
尽管这篇文章提出的网格几何谱压缩方法具有一定的优势，但也存在一些不足之处：

压缩比例的限制： 该方法在选择要保留的特征向量数量时，依赖于预设的压缩比例。这可能导致在一些情况下，无法达到较高的压缩比例要求。
计算复杂度： 文章未详细探讨该方法的计算复杂度。由于谱分解等操作可能较为耗时，该方法在大规模网格数据上的计算效率仍然需要进一步研究和改进。

综上所述，这篇文章介绍了一种利用网格谱性质进行几何压缩的方法。相比以前的方法，该方法具有高效性和几何质量保持的优势。然而，仍然存在一些不足，包括压缩比例的限制和计算复杂度方面的待改进之处。

High-Pass Quantization for Mesh Encoding

文章概述：
这篇文章介绍了一种称为"High-Pass Quantization for Mesh Encoding"的方法，用于对网格进行编码和压缩。该方法利用高通滤波器和量化技术，通过保留网格的高频细节信息来实现高效的压缩。作者通过实验证明了该方法在减小网格数据尺寸的同时，能够保持较高的几何质量和视觉效果。

技术要点：

高通滤波器的应用： 该方法使用高通滤波器对网格进行处理，以保留高频细节信息。高通滤波器可以滤除低频成分，使得编码过程更加集中于网格的细节部分，从而实现更高效的压缩。
量化技术： 文章采用了一种基于量化的编码策略。通过将高频细节信息进行量化，将连续的浮点数值转换为离散的整数值，从而减小数据的表示和存储开销。同时，为了保持编码的质量，文章提出了一种自适应的量化策略，根据网格的局部特征调整量化的精度。
编码算法： 文章提出了一种基于高通滤波和量化的编码算法。首先，通过高通滤波器处理网格，提取高频细节信息。然后，对提取的高频细节信息进行自适应量化，得到离散的整数值。最后，将量化后的数据进行编码和压缩，以减小存储空间。

相比以前方法的改进：
相较于以前的方法，这篇文章提出的High-Pass Quantization for Mesh Encoding方法具有以下改进：

高频细节保留： 传统的网格编码方法通常只关注低频成分，而该方法通过使用高通滤波器，专注于保留高频细节信息。这样可以更好地捕捉网格的细节特征，提高几何质量和视觉效果。
自适应量化： 文章提出了一种自适应的量化策略，根据网格的局部特征调整量化的精度。这种自适应性可以更好地平衡压缩比和几何质量，提供更好的编码效果。

文章的不足：
尽管该方法在网格编码和压缩方面有一定的优势，但仍存在一些不足之处：