1. 引言：快速排序的背景与重要性

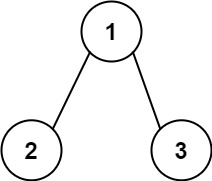
快速排序（Quick Sort）是一种高效的排序算法，以其出色的性能和普适性而受到广泛关注。它利用了分而治之的思想，通过将数组分割成较小的子数组，并将这些子数组分别排序来实现整体的排序。本文将深入探讨快速排序的原理、步骤以及其在实际中的应用，为您展示一种高效的排序方法。

探寻分治法https://blog.csdn.net/qq_45467165/article/details/132453575?spm=1001.2014.3001.5501

2. 快速排序的原理与步骤

快速排序的核心思想是通过“分区”来排序。它选择一个基准元素（pivot），将数组分成小于基准的左子数组和大于基准的右子数组。然后，递归地对左右子数组进行排序，最终实现整个数组的有序。

2.1 分区过程

分区是快速排序的第一步。在分区过程中，我们选择一个基准元素，通常是数组的第一个或最后一个元素。然后，通过重排数组，将小于基准的元素移到基准的左边，将大于基准的元素移到基准的右边。最终，基准元素处于其正确的位置，左边是小于它的元素，右边是大于它的元素。

2.2 递归排序

在分区完成后，我们得到了一个基准元素的正确位置，接着我们递归地对左右子数组进行排序。即对左子数组和右子数组分别应用快速排序算法，直到每个子数组的长度为1或为空。

2.3 原理

快速排序是一种高效的排序算法，它基于分治法（Divide and Conquer）的思想。分治法将问题分解成更小的子问题，递归地解决这些子问题，最终将它们的解合并得到整体问题的解。在快速排序中，我们选择一个基准元素，将数组分成小于基准的左子数组和大于基准的右子数组，然后递归地对左右子数组进行排序，最后合并得到有序数组。

2.4 步骤

以下是快速排序的步骤：

选择基准元素： 从待排序数组中选择一个基准元素，通常选择第一个或最后一个元素。
分区操作： 将数组分成两个子数组，一个小于基准的左子数组，一个大于基准的右子数组。通过分区操作，基准元素的最终位置也确定了。
递归排序： 对左子数组和右子数组分别应用快速排序算法，递归地将它们排序。
合并子数组： 递归排序完成后，将左子数组、基准元素和右子数组合并起来，得到完整的有序数组。

3. 快速排序的代码示例

我们通过一个简单的代码进行分析：

#include <iostream>
using namespace std;

// 分区函数，将数组分成小于基准和大于基准的两部分
int partition(int arr[], int low, int high) {
    int pivot = arr[low];  // 选择第一个元素作为基准
    int i = low + 1;  // 大于基准的元素的索引
    for (int j = low + 1; j <= high; j++) {
        if (arr[j] < pivot) {
            swap(arr[i], arr[j]);
            i++;
        }
    }
    swap(arr[low], arr[i - 1]);
    return i - 1;
}

// 快速排序函数
void quickSort(int arr[], int low, int high) {
    if (low < high) {
        int pi = partition(arr, low, high);
        quickSort(arr, low, pi - 1);
        quickSort(arr, pi + 1, high);
    }
}

int main() {
    int arr[] = {10, 7, 8, 9, 1, 5};
    int n = sizeof(arr) / sizeof(arr[0]);
    quickSort(arr, 0, n - 1);
    cout << "Sorted array: ";
    for (int i = 0; i < n; i++) {
        cout << arr[i] << " ";
    }
    return 0;
}

4. 快速排序的复杂度分析

4.1 时间复杂度

快速排序的平均时间复杂度为 O(n log n)，其中 n 是待排序数组的长度。在分区过程中，每次都能将数组划分成两部分，因此分区的时间复杂度是 O(n)。在最坏情况下，即每次分区都只能将数组分成一个元素和其他元素两部分，快速排序的时间复杂度退化为 O(n^2)。但在实际中，快速排序的平均时间复杂度为 O(n log n)，具有良好的性能。