题目: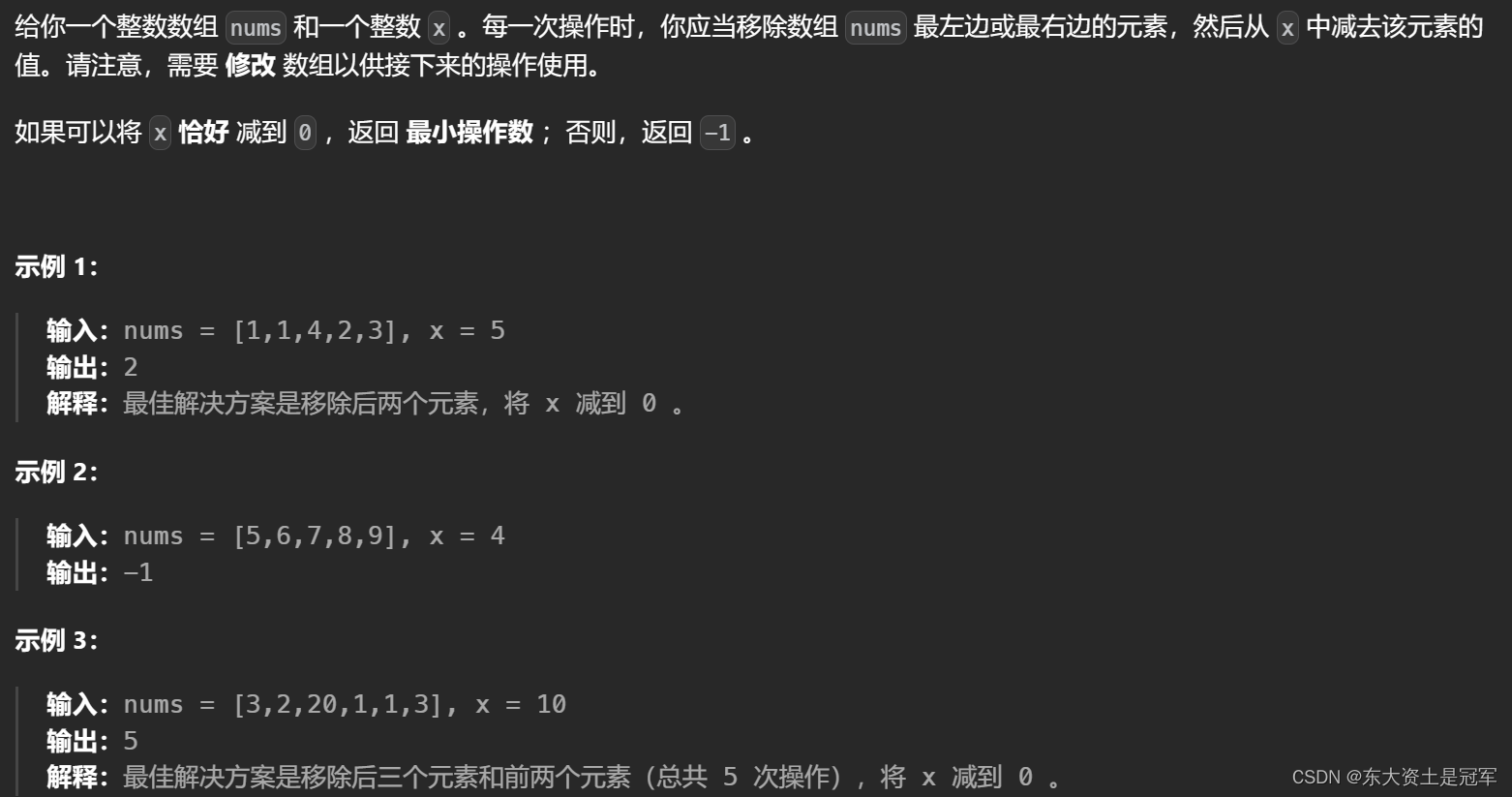

算法分析:

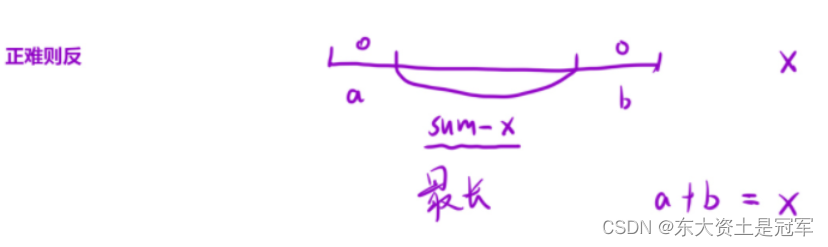
可以看出,这道题本意是从计算两侧和为x 的数字, 要求数量最少,

那我们可以反向思考, 假如整个数组的和为sum, 那么我们就可以求中间部分和为sum-x的数字(当然必须连续), 当中间部分的数字同时达到和为sum-x以及长度最长两个要求时, 两侧数字也就达到了和为x以及数量最少的要求.

令中间部分求和结果为target

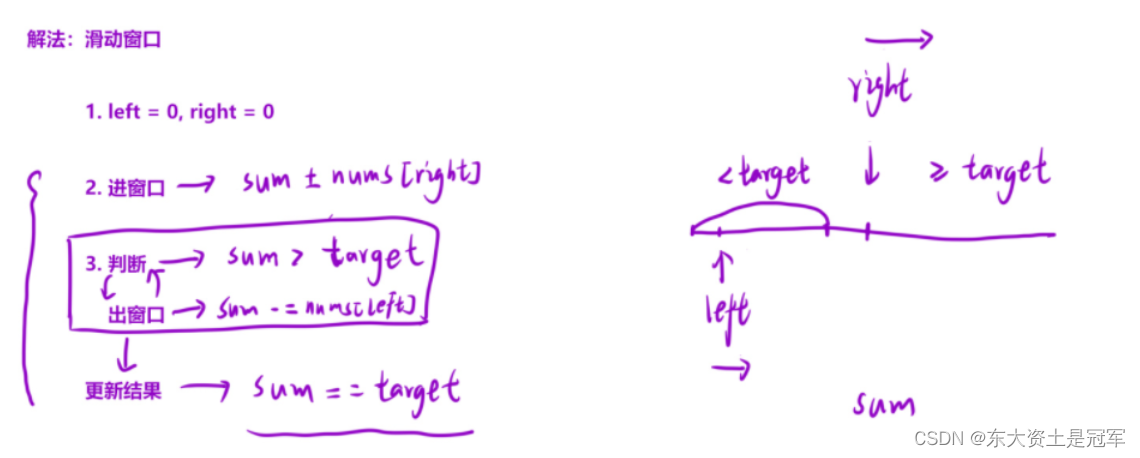
此时我们发现这正好是滑动窗口的解法

代码:

class Solution {
    public int minOperations(int[] nums, int x) {
        // int left = 0, right = 0, len = 0, sum = 0, allAdd = 0;
        // for(int i = 0; i < nums.length; i++) {
        //     allAdd += nums[i];
        // }
        // if(allAdd == x) 
        //     return nums.length;
        // while(right < nums.length) {
        //     sum += nums[right];
        //     while(sum >= allAdd - x && left < nums.length) {
        //         if(sum == allAdd - x) {
        //             len = Math.max(len, right - left + 1);
        //         }
        //         sum -= nums[left];
        //         left++;
                                        
        //     }
        //     right++;
        // }
        // return len > 0 ? nums.length - len : -1;

        int sum = 0;
        for(int a : nums) sum += a;
        int target = sum - x;

        if(target < 0) return -1;
        int ret = -1;
        for(int left = 0, right = 0, tmp = 0; right < nums.length; right++) {
            tmp += nums[right];
            while(tmp > target) {
                tmp -= nums[left++];
            }
            if(tmp == target) {
                ret = Math.max(ret, right - left + 1);
            }
        }
        if(ret == -1) {
            return -1;
        }else {
            return nums.length - ret;
        }
    }
}