前言

这次，并不是具体讨论归并排序算法，而是利用归并排序算法，探讨一下递归。归并排序的特点在于连续使用了两次递归调用，这次我们将从微观上观察递归全过程，从本质上理解递归，如果能看完，你一定能变得更强！

代码

先直接上代码吧！

using System.CodeDom.Compiler;

int _1 = 0;
int _2 = 0;

void __merge(int[] arr, int left, int mid, int right, string flag)
{ 
    Console.WriteLine($"__merge_{flag}: left={left+1}, mid={mid + 1}, right={right + 1}");
    int[] copy = new int[right - left + 1];
    //copy arr[left,right] to copy[]
    for (int ii = left; ii <= right; ii++)
    {
        copy[ii - left] = arr[ii];
    }
    int i = left;
    int j = mid + 1;
    for (int k = left; k <= right; k++)
    {
        if (i > mid)
        {
            arr[k] = copy[j-left];
            j++;
        }
        else if (j > right)
        {
            arr[k] = copy[i - left];
            i++;
        }
        else if (copy[i - left] < copy[j - left])
        {
            arr[k] = copy[i - left];
            i++;
        }
        else
        {
            arr[k] = copy[j - left];
            j++;
        }
    }
}

void __merge_sort(int[] arr, int left, int right, string flag)
{
    
    if (left >= right)
        return;

    if (flag.Contains("1"))
    {
        _1 += 1;
    }
    if (flag.Contains("2"))
    {
        _2 += 1;
    }

    int mid = (left + right) / 2;
    Console.WriteLine($"{flag}, left={left+1}, mid={mid+1}, right={right + 1}");
    __merge_sort(arr, left, mid, "第1个merge_sort");
    __merge_sort(arr, mid + 1, right, "第2个merge_sort");
    __merge(arr, left, mid, right, flag);
}


void merge_sort(int[] arr)
{
    __merge_sort(arr, 0, arr.Length - 1, "第0个merge_sort");
}

int[] arr = { 1, 3, 5, 7, 8, 2, 4, 6};
merge_sort(arr);


Console.WriteLine($"_1:{_1}||_2:{_2}");
foreach (var item in arr)
{
    Console.Write(item + " ");
}

Console.ReadLine();

递归分析

这段代码，特殊的地方在于，它使用了两次递归：

_1 和 _2 记录了 第一个和第二个递归的调用次数（和算法逻辑无关），这里增加的flag参数也主要是为了分析递归的过程。

第一个 __merge_sort 递归 的作用主要是将左边的一个数组不断的进行二分。
第二个 __merge_sort 递归 的作用主要是将右边的一个数组不断的进行二分。

merge将二分的数组按照大小顺序合二为一！

这个算法实现的难度，在于递归的构造和数组边界的把握。

宏观上看

void __merge_sort(int[] arr, int left, int right)
{
    int mid = (left + right) / 2;
    __merge_sort(arr, left, mid);
    __merge_sort(arr, mid + 1, right);
    __merge(arr, left, mid, right, flag);
}

过程就是，通过__merge_sort的递归，将数组二分，然后再将二分的数组归并。
__merge进行归并的前提是，两个即将归并的数组为已经排好序的数组！
但是，如果我们二分的到单个数字的时候，一个数字就是一个数组，这个数字也可以看成是
有序的数组。

所以，当二分到”极致的“时候，就满足了__merge的前提。

二分完成之后，以下就Merge的工作：

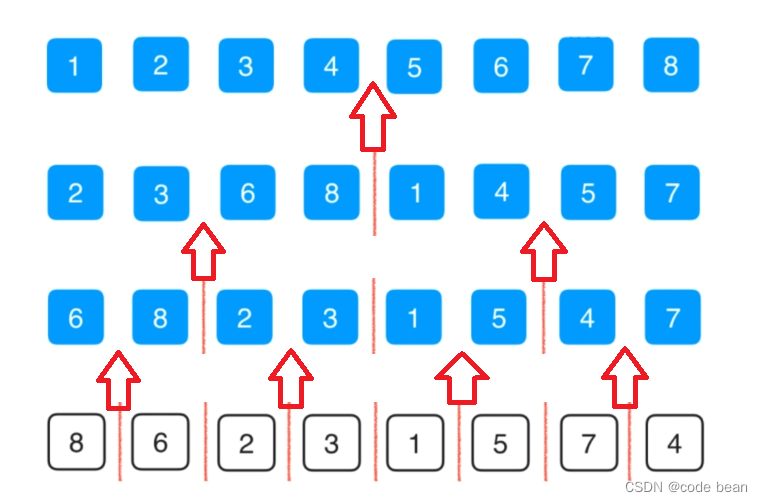
看到这张图，其实很容易联想到递归算法，但是如何构造递归函数呢？有点像：
要把大象装冰箱总共分几步？这是宏观上的看到的：
1 第一步分左边： __merge_sort(arr, left, mid);
2 第二步分右边： __merge_sort(arr, mid + 1, right);
3 第三步整合到一起： __merge(arr, left, mid, right, flag);

微观上看

我们先从微观上从本质上，看看整个递归过程是这么执行的（请结合下面两张图观看）：

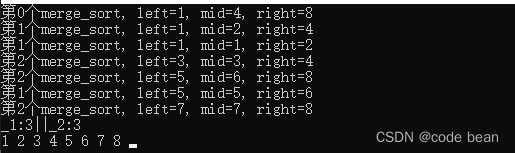
这个是程序的执行结果，第0个 表示最外层的__merge_sort被调用。
此时最左边的是1，中间为4，最右是8.
然后__merge_sort一个递归调用触发，第一个__merge_sort负责左边。
所以是：最左边的是1，中间为2，最右是4. 此时并没有满足递归退出的条件，
所以继续调用第一个__merge_sort。此时继续负责左边（注意是1 2 3 4 的左边）。
所以就有了1 1 2 ，那么很明显下次递归的时候，左边会等于右边（left >= right），所以下次就会满足递归退出的条件。

下面一段是重点：

所以下一次，开始了第二个递归的调用！他负责右边的二分。这里可能会有人觉得奇怪，不是负责右边的调用吗？怎么打印的是3 3 4 ？这是左边啊！
那我是这么理解的，递归是有层级划分的，每递归一层就像下了一层楼梯 ， 每次递归返回，就是上了一层台阶 刚刚我们退出时候，其实是处于二分 1 2 3 4 这层阶梯的，所以此时，在整个层级，需要二分的是 1 2 3 4 的右边！所以二分的是3 3 4。

此时，该层的__merge_sort也要返回到上一层了。
此时打印的是 5 6 8，直接分的就是 右边的 5 6 7 8，这是因为上一层的左边的 1 2 3 4 已经在上一次的递归中已经被分过了！（递归每一层都有自己的记忆，其实就是每一层的参数都压到栈里进行的保存）此时已经到了递归的最上层了，而且第一层的左右两边都分完了。
接下来开始，是继续往下一层递归，左边的1 2 3 4 已经二分完毕，所以是右边的 5 6 7 8，
而 5 6 7 8 也已经被 分成了 56 | 78。 所以，又是 第一个 __merge_sort 开始二分左边的 56了。
所以此时打印的是 5 5 6，最后是 第二个将右边的分为 7 7 8. 整个二分的过程就结束了。

要注意的是，两个__merge_sort始终是处于用一个层级的，当第一个__merge_sort下个几个楼梯后，其实第二个也会下同样多个阶梯。（接下来还会进一步的再次说明这一点）

合并的部分

接下来，我们来单独看看，二分之后 __merge这个函数的调用过程：


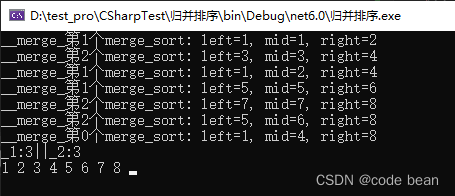
这个完全是符合预期的:
显示左边的，先合并12，再合并14，接着合并1234
然后是右边的，先合并56，再嗯好吧78，结果合并5678
最后是 148，也就是 12345678整个的合并！

现在，我们结合递归和合并一起看，是怎么样的一个顺序：

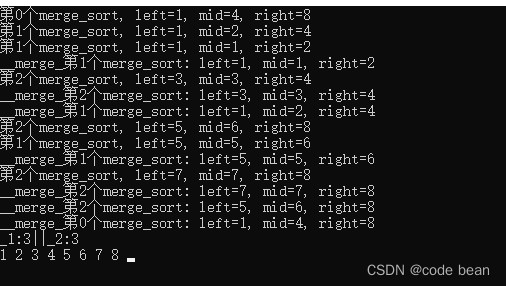
代码回顾

    int mid = (left + right) / 2;
    Console.WriteLine($"{flag}, left={left+1}, mid={mid+1}, right={right + 1}");
    __merge_sort(arr, left, mid);
    __merge_sort(arr, mid + 1, right);
    __merge(arr, left, mid, right, flag); } ```

首先是，第一次__merge_sort 三次连续的递归之后，直接就开始了第一次的合并！
这里，可能有人会问：按照函数的调用顺序，此时不应该执行，第二个__merge_sort吗？这么直接调到了
__merge函数了？第二个__merge_sort不会执行吗？

这里，我再次强调层级的问题，现在已经递归到最后一个层级了，此时left mid right
对应的是 1 1 2，其实就是对 12 进行二分，此时 对应在这个层级的第二个__merge_sort来说：
__merge_sort(arr, mid + 1, right);
left = mid+1 所以此时，满足了递归的退出条件 left >= right,（其实就是只剩下2了不用你右边在分了！）
所以此时不是第二个__merge_sort没有调用，而是直接退出了。（递归的退出条件也是递归的最重要的核心之一）
所以就执行的__merge，完成12合并（合并的过程其实就排序，可以参考最上面的__merge代码）。

此时，递归已经触底的，开始返回到上一次，上一层的左边已经递归完成（12已经二分，也满足递归退出条件）所以上一层阶梯，就开始右边的递归，将34 二分（注意：这里124左右的划分全部结束啦），二分完成后就返回了，
于是就会执行__merge，完成 34的合并。在这次，__merge结束后，紧接着又是一个
__merge，完成 1 2 4 的合并，也就是说，前面两个__merge_sort都被跳过了！
这是为啥？

这是因为__merge执行完后，此时递归又会上一个层级，在这个层级，其实就是1 2 4的二分，
而 1 2 4 左和右的划分在之前的递归过程中已经结束了，所以直接开始合并了。

此时，还剩下的部分是：


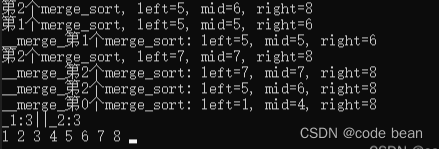
合并完成之后，这一次递归也返回了，就到了最上面一层递归了，不过左边的部分已经执行过了，所以是，右边的 5 6 8 的 划分，划分玩之后，从第二个__merge_sort，再次进入递归（下一层楼梯）此时遇到了下一层的第一个__merge_sort。于是就有了 5 5 6，已经触底了所以返回遇到了这一层的第二个__merge_sort就有了 778。到此两个递归都已经触底且都已完成，接下来就都是merge合并了！

这里说一些感想，读到这里你应该体会到了调用两个递归的特点，一开始遇到第一个递归，就会一直递归到最下面一层，然后一层层返回，如下：
在返回的过程中会调用 倒数第二层的第二个__merge_sort， 所以第一个__merge_sort，在递归下楼梯的时候调用，而第二个递归是在上楼梯的时候调用，而当上到最上层的时，刚刚调用完了第二个__merge_sort，又会进入递归的下一层，并碰再次遇到第一个__merge_sort，并再次进入第一层递归！再次触底！

次数问题

接下来再看另外一个问题（和递归无关）如果把数组扩大到10：


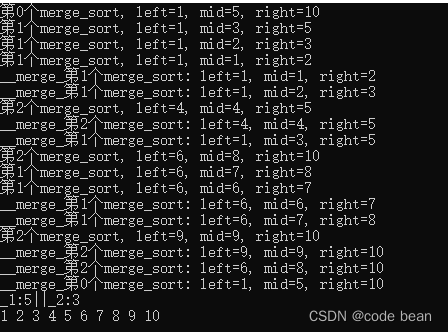
这次，负责左边的递归运行了5次，而负责右边的只运行了3次。这次左右不平衡了？
会觉得奇怪吗？
这是因为奇偶数的问题，当 数组为8的时候， 8 二分 后是 4+ 4，最后变成 2+2+2+2。
在变成单个之前都是偶数。如果是10，二分就会变成5。5这个数字就会导致二分时，左边的二分次数会更多。
所以只有当个数为 2的N次方的时候，比如 8 16，这样的数组长度时，两次递归的调用次数才会相同！

递归小结

看到，最后你还能回忆起，__merge_sort是如何实现二分的吗？
想不起来，没关系，因为这个过程很隐秘，不过也是递归的设计的关键所在。

void __merge_sort(int[] arr, int left, int right)
{
    int mid = (left + right) / 2;
    __merge_sort(arr, left, mid);
    __merge_sort(arr, mid + 1, right);
    __merge(arr, left, mid, right, flag);
}

首先，我们要自己设计递归函数，比如传入一个数组，我们的目的是改变该数组内部的元素的顺序，但是，每次考虑的是其中的一个部分。所以我需要一个边界，left和right。
对于整个数组来说，left是0，right是长度-1；
二分之后，每次二分之后，left和right都会发生变化。
每次递归调用都会下一层阶梯，进入下一层，从而导致left和right的再次改变。
能理解 ”进入下一层“ 是理解递归的关键，在一次次递归中，就完成了二分的过程！
我们，可先从宏观上设计思路，再从微观上确保思路的正确。

这篇文章，写了很久，自我感觉良好，不知道各位觉得如何，欢迎评论区反馈~~~

附加，在提供一下完整的python代码吧

之前本来是用python测试，不过还是觉得vs调试C#方便啊：

def __merge(arr, left, mid, right):
    arr_copy = arr[left:right + 1][:]
    i = left
    j = mid+1
    for k in range(left, right+1):
        if i > mid:
            arr[k] = arr_copy[j-left]
            j = j + 1
        elif j > right:
            arr[k] = arr_copy[i-left]
            i = i + 1
        elif arr_copy[i-left] < arr_copy[j-left]:
            arr[k] = arr_copy[i-left]
            i = i + 1
        else:
            arr[k] = arr_copy[j-left]
            j = j + 1


def __merge_sort(arr, left, right):
    if left >= right:
        return
    mid = (left + right) // 2
    print(left, mid, right)
    __merge_sort(arr, left, mid)
    __merge_sort(arr, mid + 1, right)
    __merge(arr, left, mid, right)


def merge_sort(arr):
    __merge_sort(arr, 0, len(arr) - 1)


if __name__ == '__main__':
    arr0 = [1, 3, 5, 7, 9, 2, 4, 6, 8, 10]
    merge_sort(arr0)
    print(arr0)