import cv2 as cv
import numpy as np
import matplotlib.pyplot as plt

img = cv.imread("../SampleImages/pomeranian.png", cv.IMREAD_COLOR)
print(img.shape)

#图像直方图计算
#cv.calcHist(images, channels, mask, histSize, ranges, hist, accumulate)
#images：原图像（图像格式为 uint8 或 float32）。当传入函数时应该 用中括号 [] 括起来，例如：[img]。
#channels：同样需要用中括号括起来，它会告诉函数我们要统计那幅图 像的直方图。如果输入图像是灰度图，它的值就是 [0]；如果是彩色图像 的话，传入的参数可以是 [0]，[1]，[2] 它们分别对应着通道 B，G，R。
#mask: 掩模图像。要统计整幅图像的直方图就把它设为 None。但是如 果你想统计图像某一部分的直方图的话，你就需要制作一个掩模图像，并 使用它。
#histSize：BIN 的数目。也应该用中括号括起来，例如：[256]。
#ranges: 像素值范围，通常为 [0，256]
#hist：是一个 256x1 的数组作为返回值，每一个值代表了与次灰度值对应的像素点数目。
#accumulate：是一个布尔值，用来表示直方图是否叠加。
#参考资料：https://blog.csdn.net/yukinoai/article/details/87900860
hist_b = cv.calcHist([img], [0], None, [256], [0,256])
hist_g = cv.calcHist([img], [1], None, [256], [0,256])
hist_r = cv.calcHist([img], [2], None, [256], [0,256])
#显示图像
fig,axes = plt.subplots(nrows=2, ncols=2, figsize=(10,10), dpi=100)
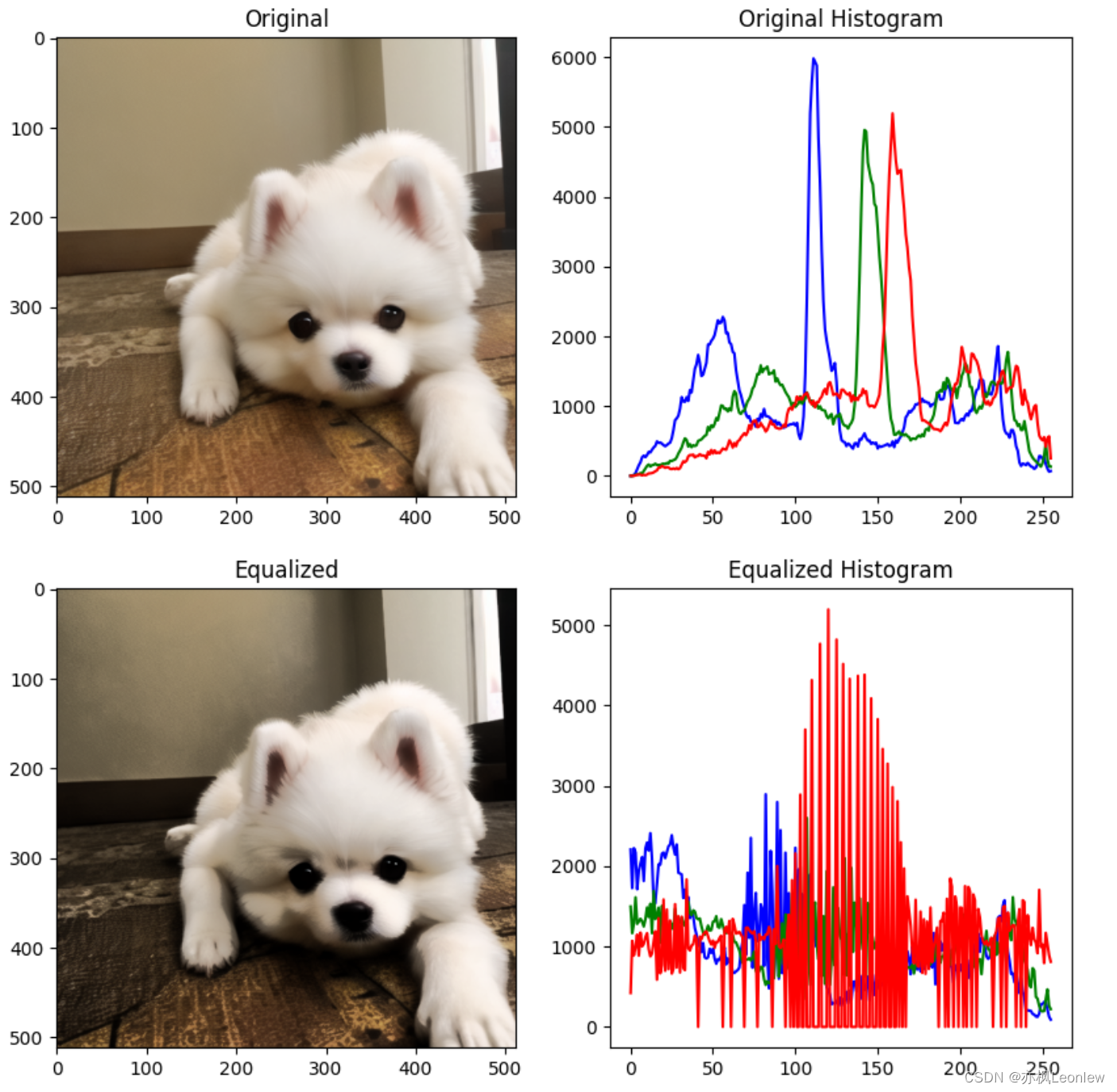
axes[0][0].imshow(img[:,:,::-1])
axes[0][0].set_title("Original")
axes[0][1].set_title("Original Histogram")
axes[0][1].plot(hist_b, color='b')
axes[0][1].plot(hist_g, color='g')
axes[0][1].plot(hist_r, color='r')

#彩色图像直方图均衡化
#cv.equalizeHist(src)
#参考资料：https://blog.csdn.net/qq_37701443/article/details/103564379
def RGBImageHistEqualize(src):
    hsv = cv.cvtColor(src, cv.COLOR_RGB2HSV)
    channels = cv.split(hsv)
    #对亮度通道进行直方图均衡化
    cv.equalizeHist(channels[2], channels[2])
    hsv = cv.merge(channels)
    src = cv.cvtColor(hsv, cv.COLOR_HSV2RGB)
    return src
img_hist_equalized = RGBImageHistEqualize(img)
hist_equalized_b = cv.calcHist([img_hist_equalized], [0], None, [256], [0,256])
hist_equalized_g = cv.calcHist([img_hist_equalized], [1], None, [256], [0,256])
hist_equalized_r = cv.calcHist([img_hist_equalized], [2], None, [256], [0,256])

#显示直方图均衡化后的结果
axes[1][0].imshow(img_hist_equalized[:,:,::-1])
axes[1][0].set_title("Equalized")
axes[1][1].set_title("Equalized Histogram")
axes[1][1].plot(hist_equalized_b, color='b')
axes[1][1].plot(hist_equalized_g, color='g')
axes[1][1].plot(hist_equalized_r, color='r')