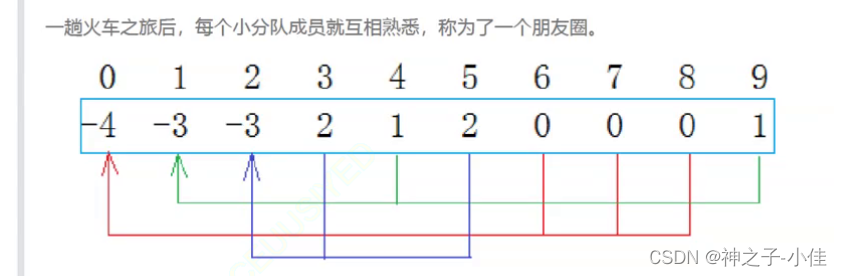
并查集的概念

将n个不同的元素划分成一些不相交的集合。开始时，每个元素自成一个单元元素集合，然后按一定的规律将归于同一组元素的集合合并。在此过程中反复遇到查询某一个元素属于那个集合的运算，这种抽象的数据类型称为并查集。
主要思想：用集合中的一个元素代表集合。

代码实现

#include<iostream>
#include<vector>
class UnionFindSet
{
public:
	UnionFindSet(size_t n)//构造函数
		:_ufs(n,-1)
	{}
	void Union(int x1,int x2)//合并根
	{
		int root1 = FindRoot(x1);
		int root2 = FindRoot(x2);
		if (root1 == root2)//如果本身在一个集合就没必要合并了	
			return;
			
		_ufs[root1] += _ufs[root2];//2个下标相加
		_ufs[root2] = root1;//存一下根的下标
		
	}
	int FindRoot(int x)//查找根
	{ 
		int parent = x;
		while (_ufs[parent] >= 0)//说明不是根
		{
			parent = _ufs[parent];
		}
		return parent;//f返回的编号是负数就是根
	}
	bool InSet(int x1, int x2)
	{
		return FindRoot(x1) == FindRoot(x2);//相等说明同一个根在同一个集合
	}
	size_t SetSize()//有几个集合
	{
		size_t size = 0;
		for (size_t i = 0; i < _ufs.size(); ++i)
		{
			if (_ufs[i] < 0)//判断有几个负数就有几个集合,因为负数是根
			{
				++size;
			}
		}
		return size;
	}

private:
	vector<int> _ufs;//编号找人 
};