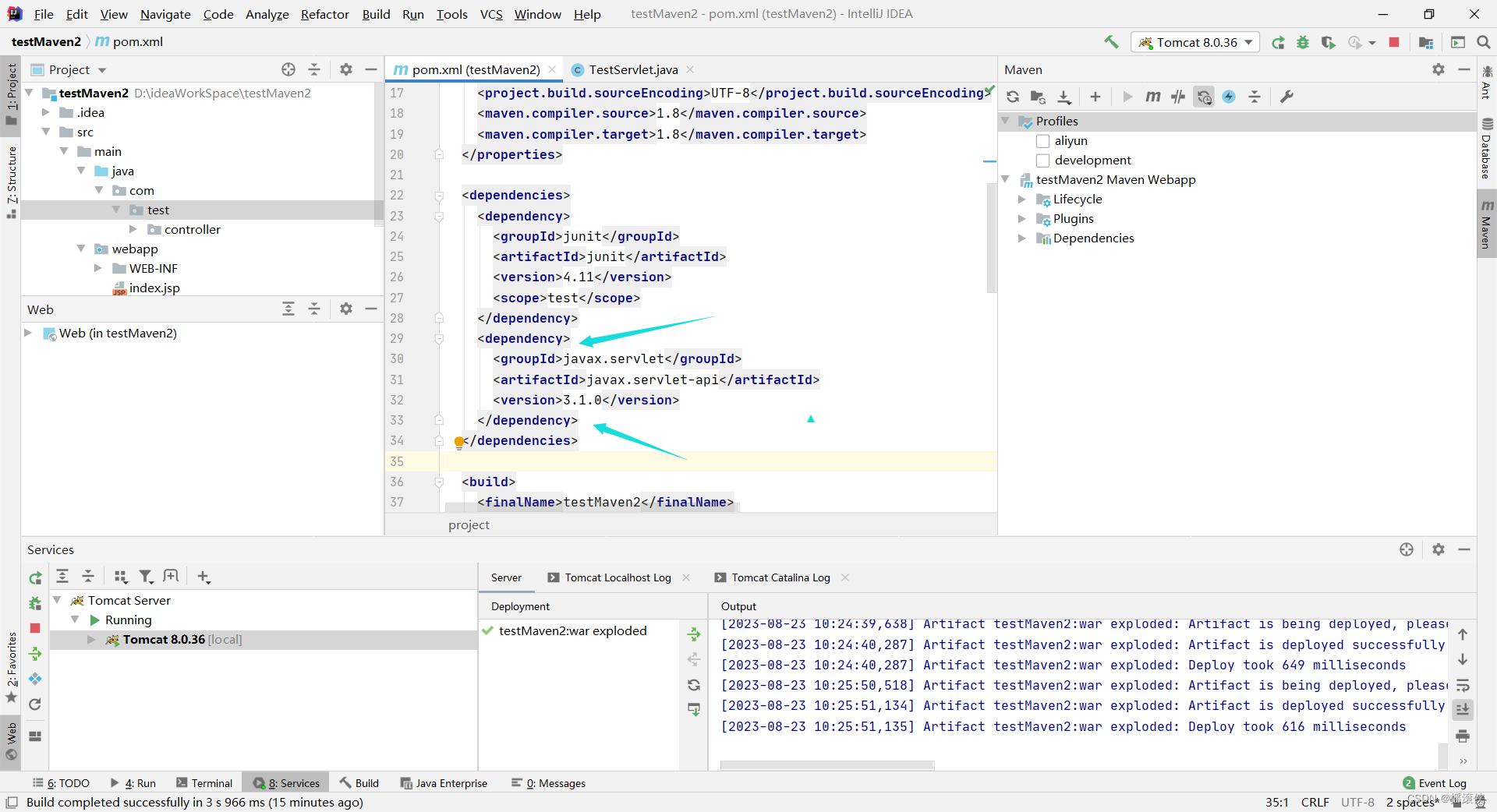
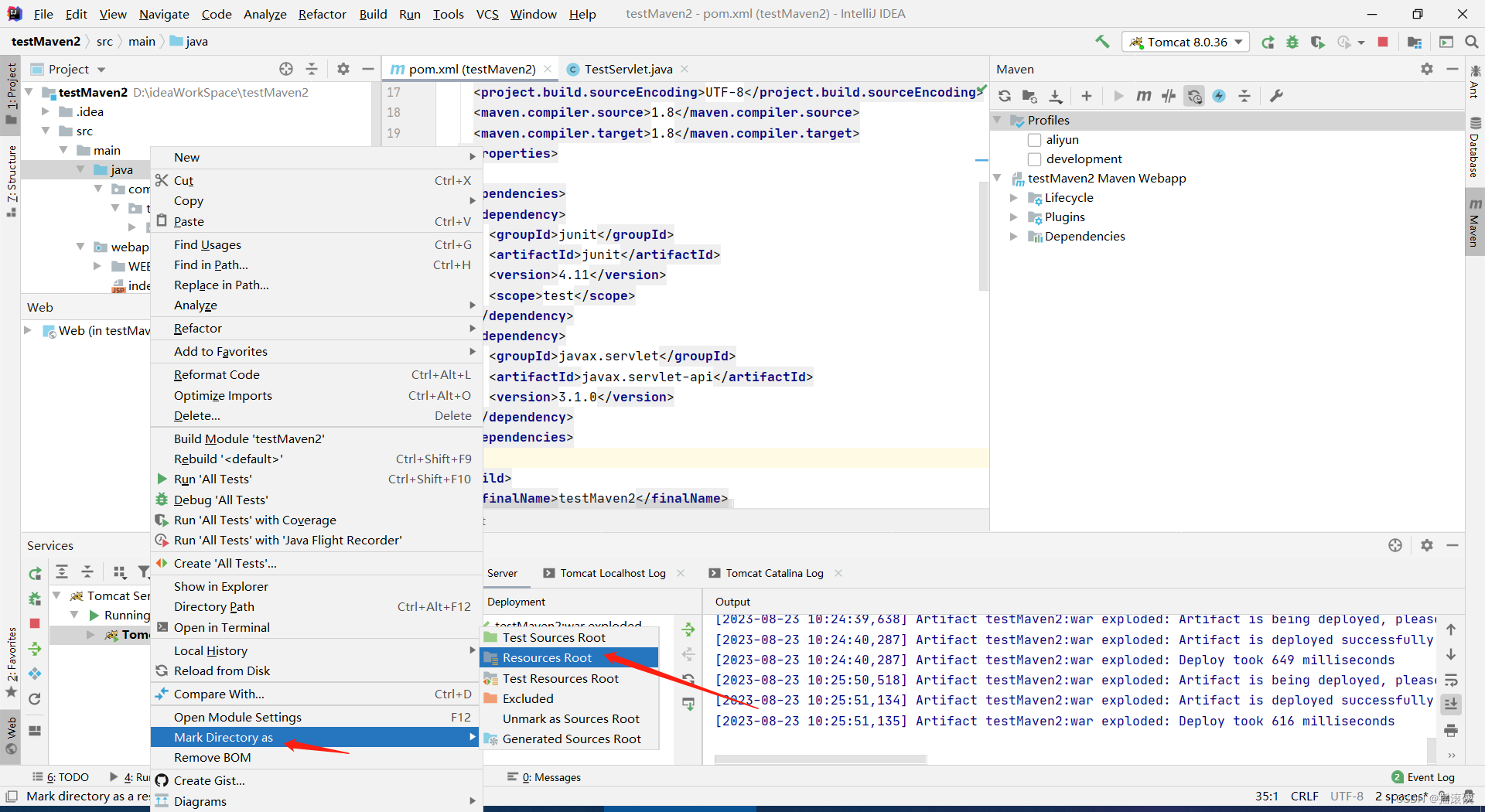
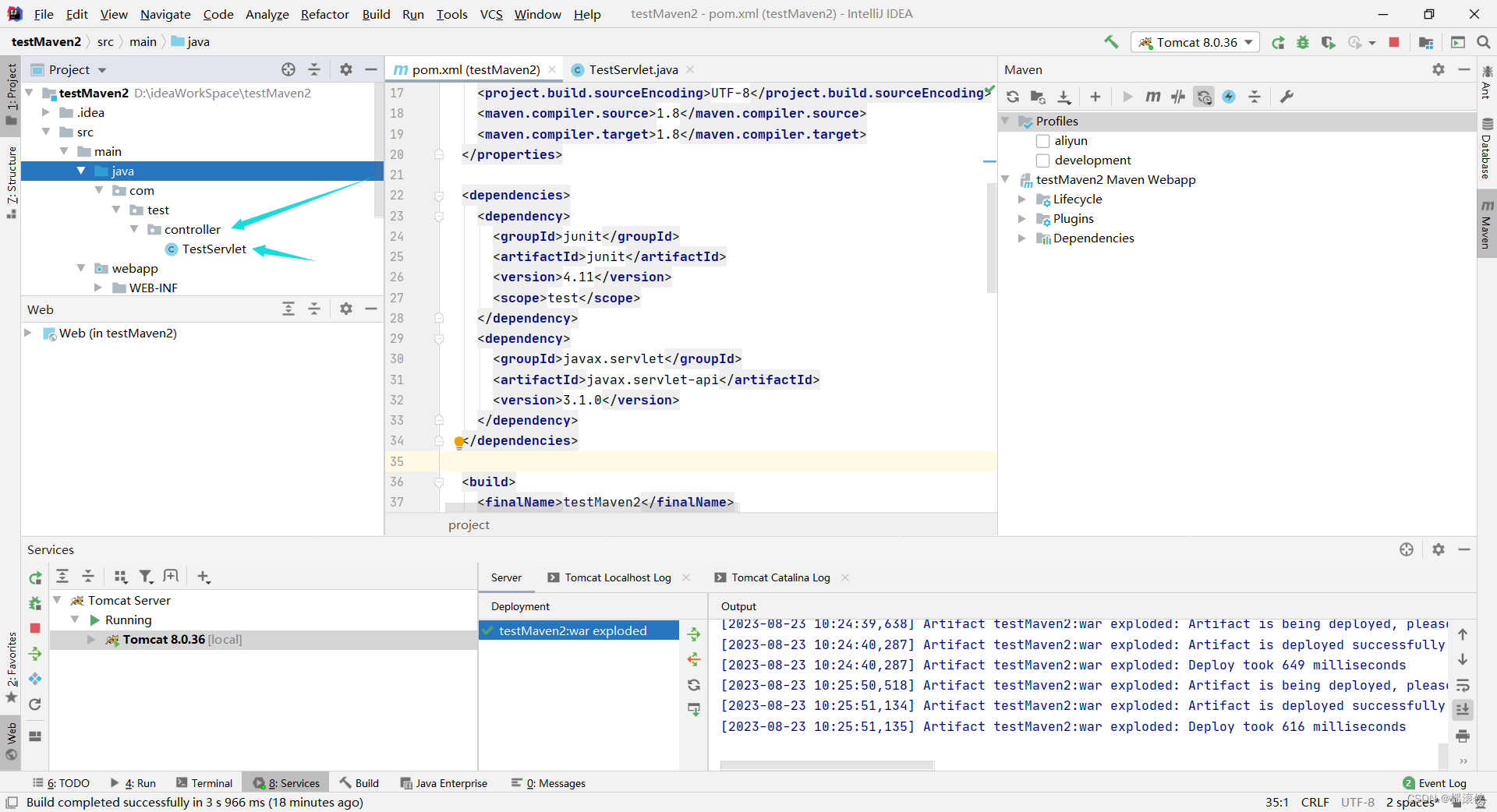
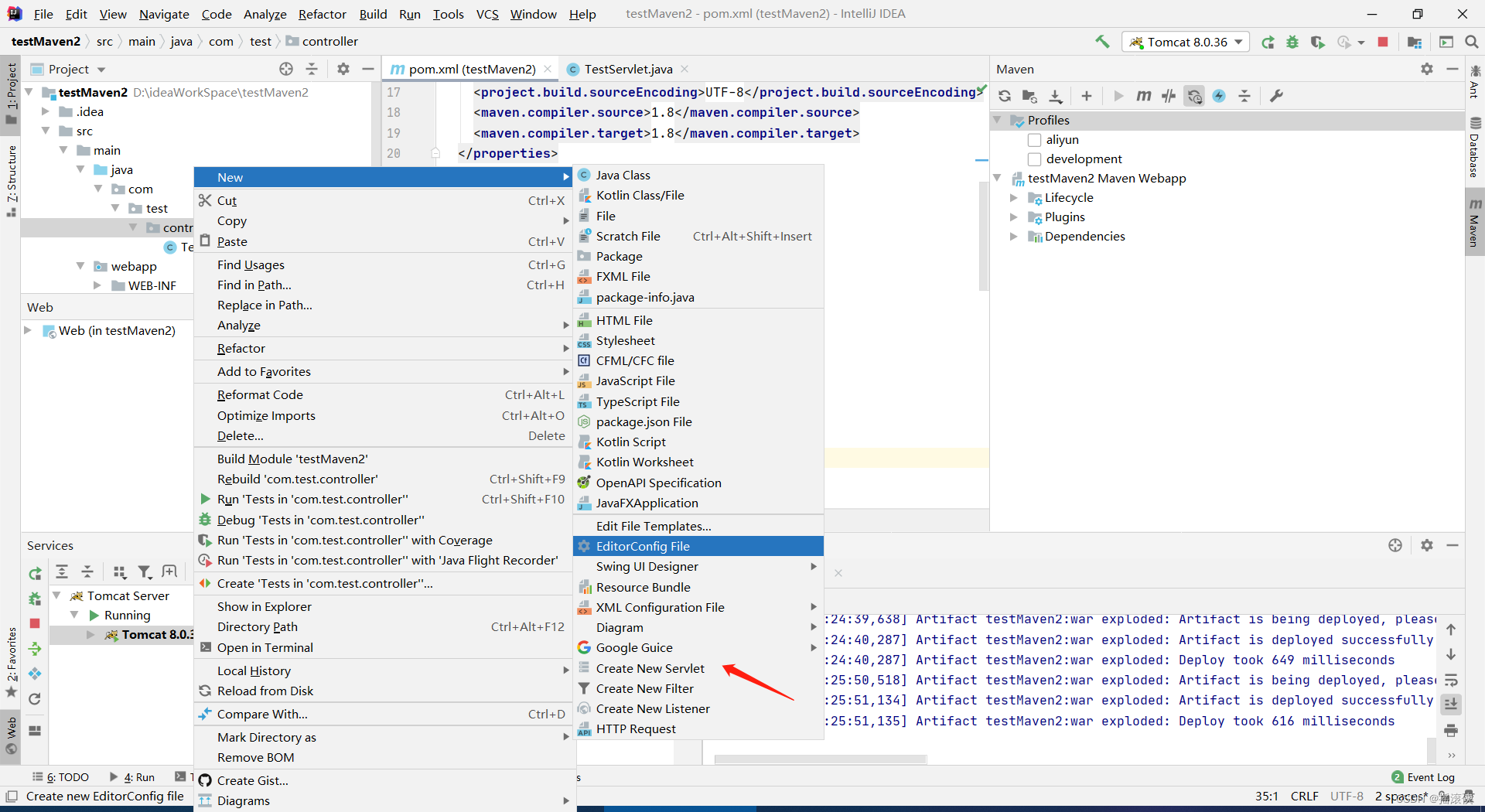
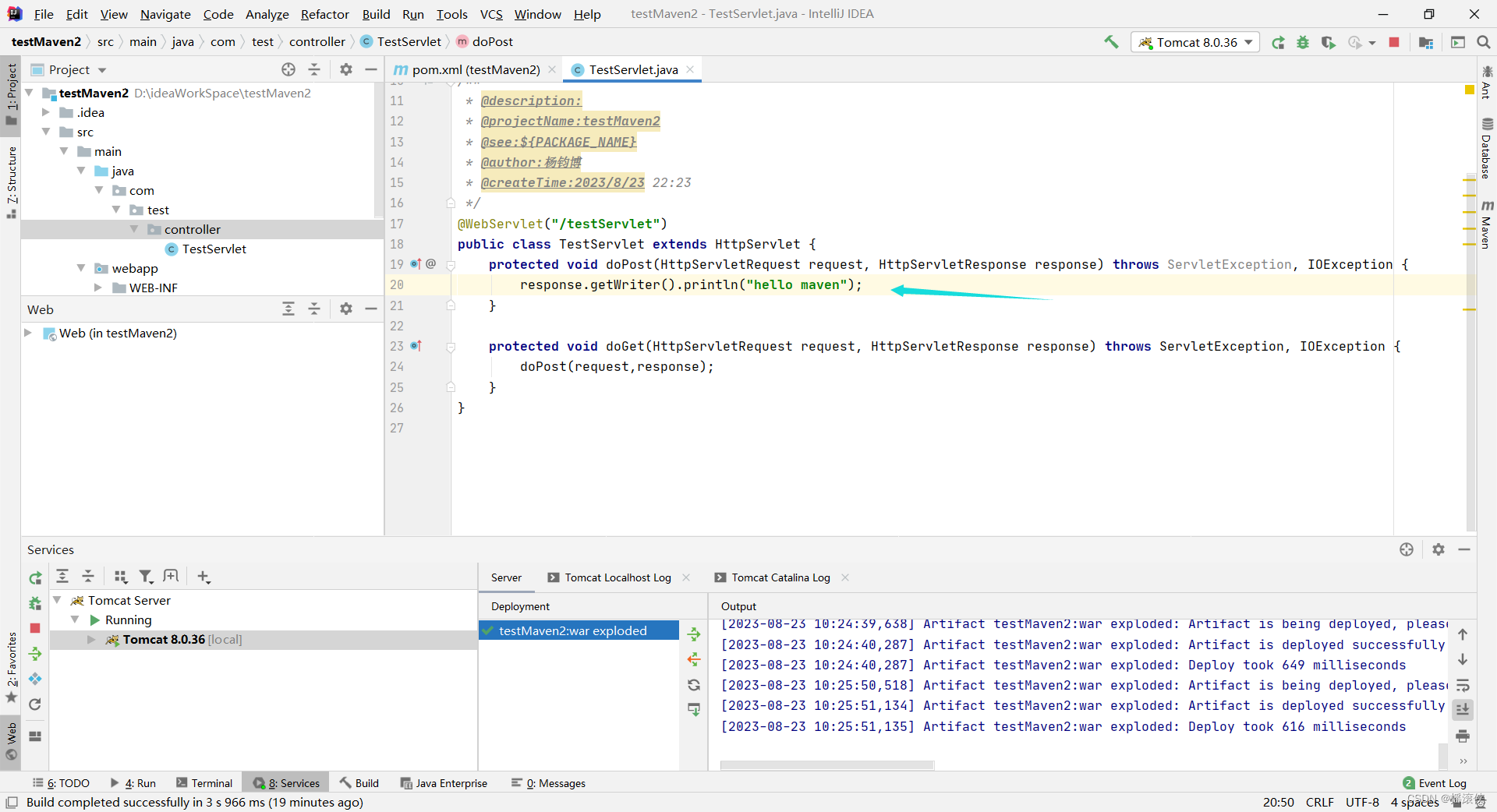
javaee idea创建maven项目,然后创建servlet
news2026/2/12 17:25:20
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/919630.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
TCP半连接队列和全连接队列
目录
什么是 TCP 半连接队列和全连接队列?
TCP 全连接队列溢出
如何知道应用程序的 TCP 全连接队列大小?
如何模拟 TCP 全连接队列溢出的场景?
全连接队列溢出会发生什么 ?
如何增大全连接队列呢 ?
TCP 半连接队列溢出
如何查看 TC…
【C#学习笔记】数据类中常用委托及接口——以List<T>为例
文章目录 List\<T\>/LinkedList \<T\>为什么是神?(泛型为什么是神)一些常见,通用的委托和接口ComparisonEnumerator List<T>/LinkedList <T>为什么是神?(泛型为什么是神࿰…
STM32 进不了main 函数
1. 我用的是STM32L151C8T6 的芯片,在github 上找了个别人的例程,拿来当模板改,由于他用的是HSE 外部晶振,我用的是内部晶振HSI,所以需要改系统时钟,改完后debug, 一直进不了main 函数࿰…
Docker容器与虚拟化技术:GitHub账户注册
目录
一、实验
1.GitHub 一、实验
1.GitHub
(1)GitHub是一个面向开源及私有软件项目的托管平台,因为只支持Git作为唯一的版本库格式进行托管,故名GitHub。
(2)官网
GitHub: Let’s build from here …
206.Flink(一):flink概述,flink集群搭建,flink中执行任务,单节点、yarn运行模式,三种部署模式的具体实现
一、Flink概述
1.基本描述
Flink官网地址:Apache Flink — Stateful Computations over Data Streams | Apache Flink
Flink是一个框架和分布式处理引擎,用于对无界和有界数据流进行有状态计算。 2.有界流和无界流 无界流(流): 有定义流的开始,没有定义结束。会无休止…
Apache StreamPark系列教程第一篇——安装和体验
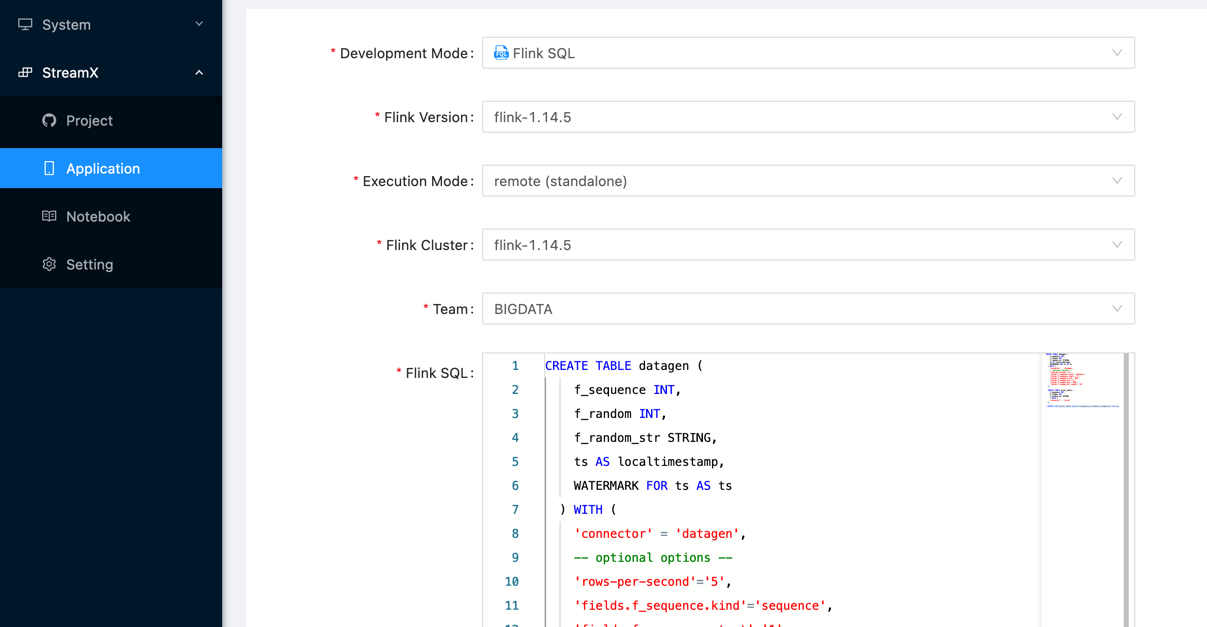
一、StreamPark介绍
实时即未来,在实时处理流域 Apache Spark 和 Apache Flink 是一个伟大的进步,尤其是Apache Flink被普遍认为是下一代大数据流计算引擎, 我们在使用 Flink & Spark 时发现从编程模型, 启动配置到运维管理都有很多可以抽象共用的地方, 我们将一些好的经验…
机器学习中XGBoost算法调参技巧
本文将详细解释XGBoost中十个最常用超参数的介绍,功能和值范围,及如何使用Optuna进行超参数调优。
对于XGBoost来说,默认的超参数是可以正常运行的,但是如果你想获得最佳的效果,那么就需要自行调整一些超参数来匹配你…
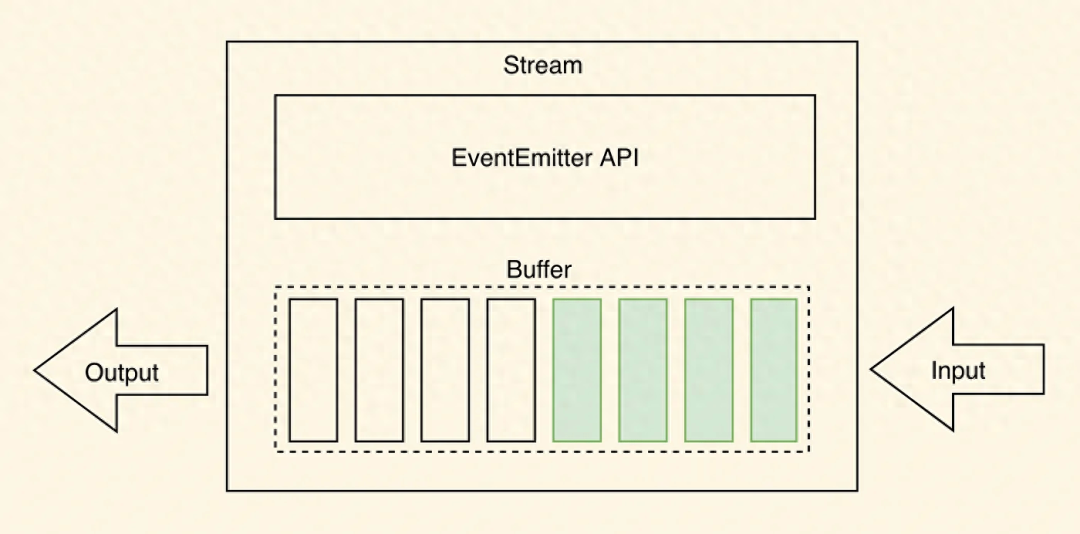
如何深入理解 Node.js 中的流(Streams)
Node.js是一个强大的允许开发人员构建可扩展和高效的应用程序。Node.js的一个关键特性是其内置对流的支持。流是Node.js中的一个基本概念,它能够实现高效的数据处理,特别是在处理大量信息或实时处理数据时。 在本文中,我们将探讨Node.js中的流…
es和数据库同步方案
5.5 课程信息索引同步
5.5.1 技术方案
通过向索引中添加课程信息最终实现了课程的搜索,我们发现课程信息是先保存在关系数据库中,而后再写入索引,这个过程是将关系数据中的数据同步到elasticsearch索引中的过程,可以简单成为索引…
SD-WebUI和ComfyUI的局域网访问设置!
如何通过局域网访问AI绘画软件,这是星球成员提的一个问题,而且两个软件都问到了,我也回答过了。现在把内容整理一下发出来,大家可能用得着。 SD-WebUI和ComfyUI这两个AI绘画工具都是通过浏览器来使用,但是默认情况下并…
oops Framwork creator游戏开发框架
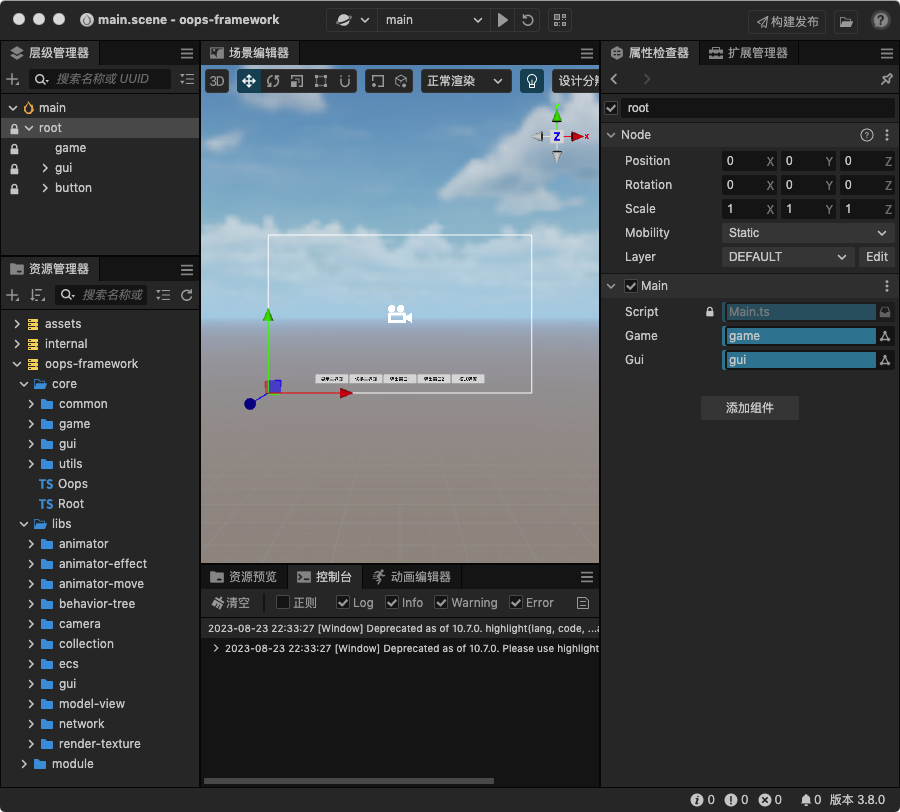
环境: Mac oops Framework
该框架是由gdflas编写,基于cocosCreator 3.x 而实现的开源游戏框架。特点:
框架通过插件方式提供,与项目相分离,方便不同版本平滑升级内置模块低耦合, 可根据需要进行删减&…
如何使用HTML5新增的标签来构建语义化的页面结构?
聚沙成塔每天进步一点点 ⭐ 专栏简介⭐ <header>:⭐ <nav>:⭐ <main>:⭐ <section>:⭐ <article>:⭐ <aside>:⭐ <footer>:⭐ <figure> 和 &l…
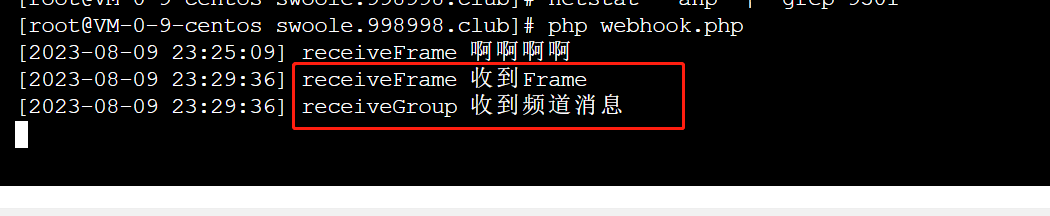
开黑啦kook 机器人开发 PHP swoole Liunx 服务器(宝塔)
安装环境 PHP 拓展 直接使用 宝塔一键安装 (Windows系统不支持)
设置命令行的PHP版本避免执行脚本时 获取不到 swoole 检查swoole是否安装成功 获取官方SDK
GitHub - kaiheila/php-bot: 开黑啦机器人的php版本https://github.com/kaiheila/php-bot 配…
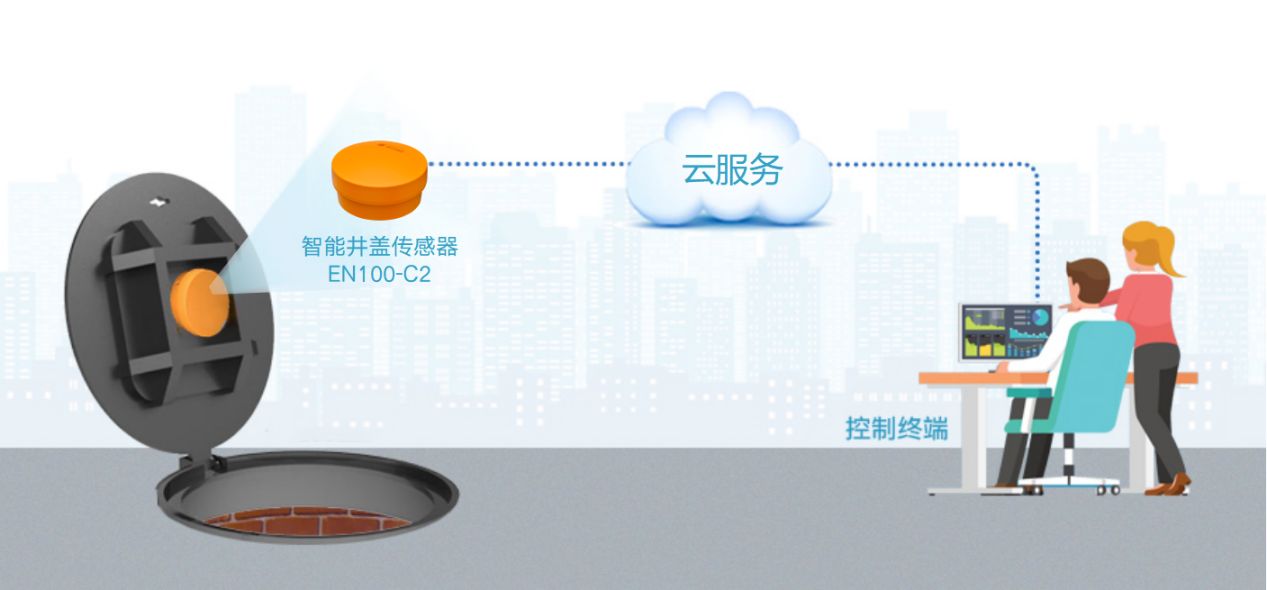
智能井盖传感器,物联网智能井盖系统
随着城市人口的不断增加和城市化进程的不断推进,城市基础设施的安全和可靠性变得愈发重要,城市窨井盖作为城市基础设施重要组成部分之一,其安全性事关城市安全有序运行和居民生产生活安全保障。 近年来,各地都在加强城市窨井盖治理…
多页面应用多次引入同一个资源优化方法
介绍
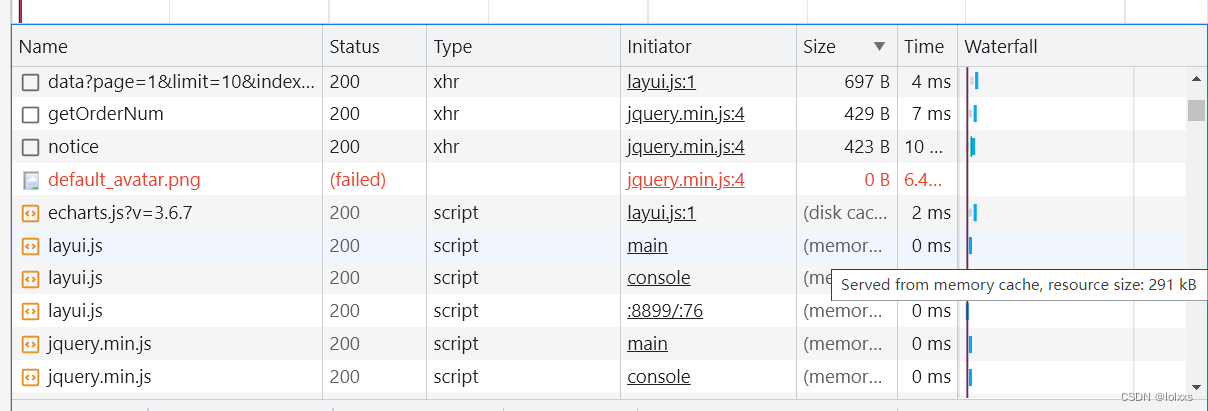
项目是多页面应用,每个界面都会引入一次layui框架源码,造成未优化之前界面加载十分缓慢
优化探索
想办法让多页面只加载一次
但是由于多页面使用iframe,主页面和子页面资源隔离,无法让资源只加载一次
利用浏览器缓存
在…
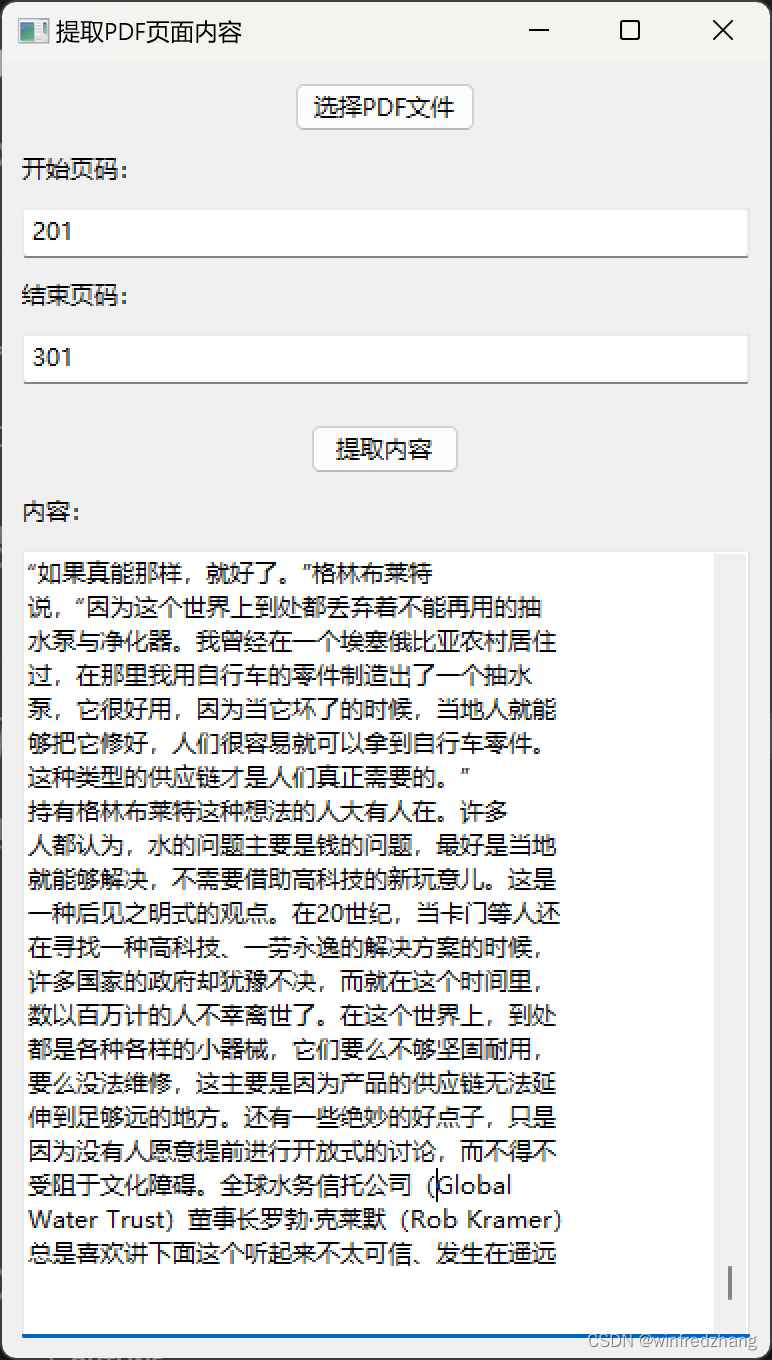
为Claude的分析内容做准备:提取PDF页面内容的简易应用程序
由于Claude虽然可以分析整个文件,但是对文件的大小以及字数是有限制的,为了将pdf文件分批传入Claude人工智能分析和总结文章内容,才有了这篇博客: 在本篇博客中,我们将介绍一个基于 wxPython 和 PyMuPDF 库编写的简易的…
计算机安全学习笔记(I):访问控制安全原理
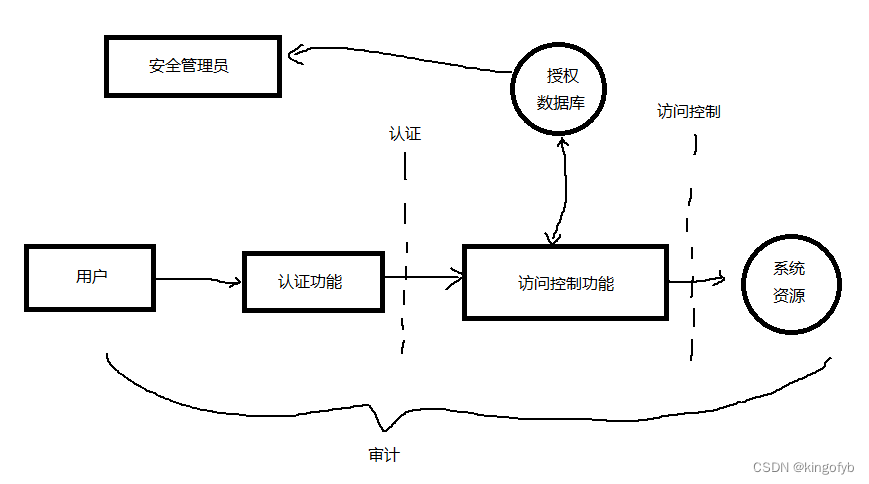
访问控制原理
从广义上来讲,所有的计算机安全都与访问控制有关。
RFC 4949: Internet Security Glossary, Version 2 (rfc-editor.org)
RFC 4949 定义的计算机安全:用来实现和保证计算机系统的安全服务的措施,特别是保证访问控制服务的措施…
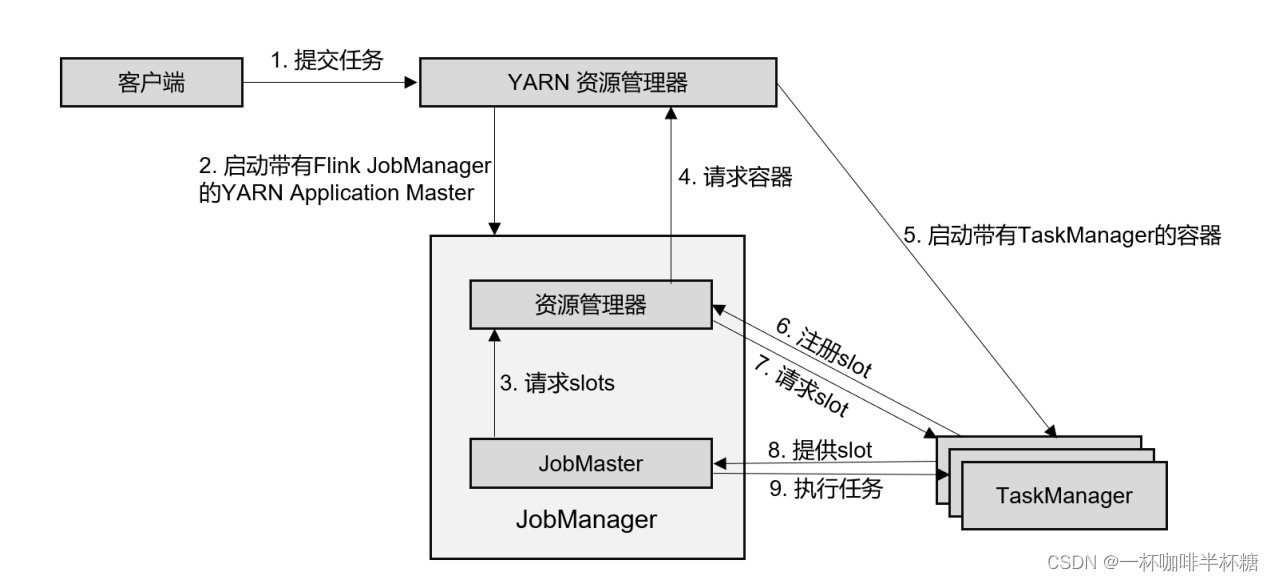
【Flink】Flink提交流程
我们通常在学习的时候需要掌握大数据组件的原理以便更好的掌握这个大数据组件,Flink实际生产开发过程中最常见的就是提交到yarn上进行调度,模式使用的Per-Job模式,下面我们就给大家讲下Flink提交Per-Job任务到yarn上的流程,流程图…
【图论】缩点的综合应用(一)
一.缩点的概念 缩点,也称为点缩法(Vertex Contraction),是图论中的一种操作,通常用于缩小图的规模,同时保持了图的某些性质。这个操作的目标是将图中的一些节点合并为一个超级节点,同时调整相关…