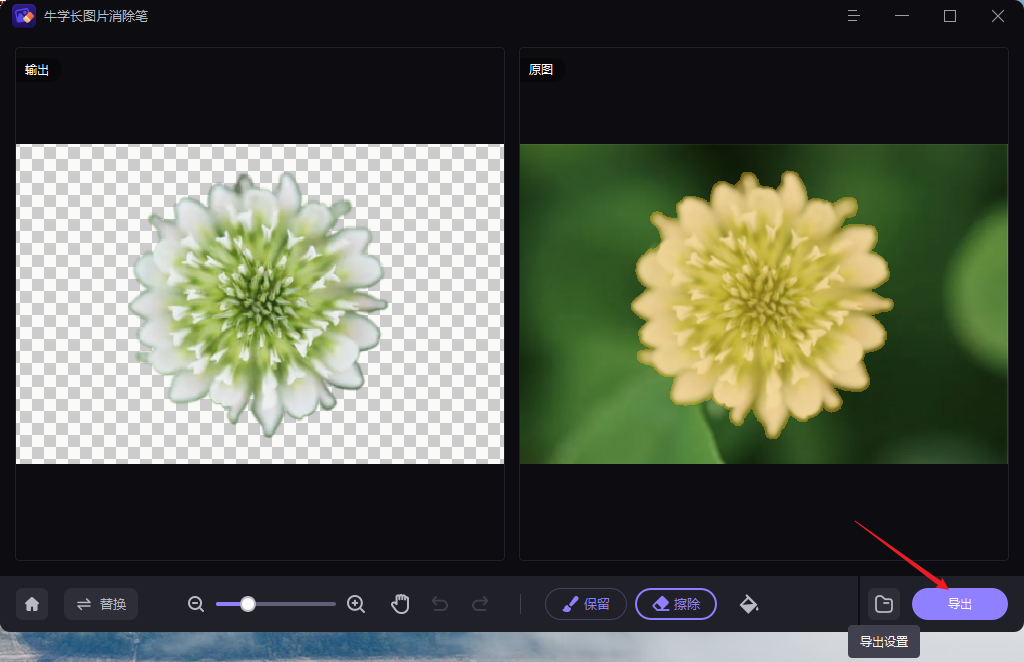
Self-organized operational neural networks (SelfONN
- 背景
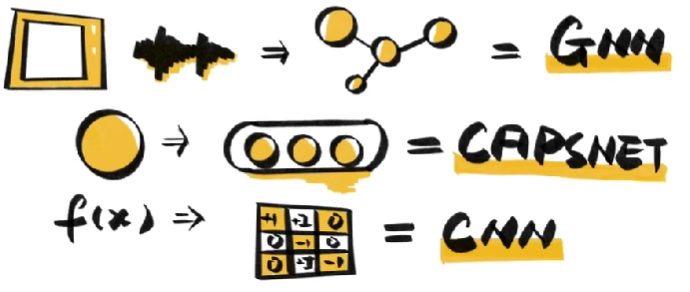
- CNN
- ONN
- SelfONN
- CNN, ONN, SelfONN对比
- SelfONN与CNN的关系
- 总结
- References
背景
本节要分享的是SelfONN, SelfONN可以看作是ONN的优化/升级, 而ONN可以看作是更一般化的CNN, 克服了CNN的一些问题。
这里先从CNN说起,
CNN

上图展示了对多通道输入的feature map进行卷积的过程, 卷积核有m个,每个卷积核实际上相当于FNN中的一个神经元, 其通道数=输入通道数, 每个卷积核对应的输出为一张feature map, 将m个卷积核的输出聚集起来即为通道数为m的feature map。
CNN存在的主要问题,
(1)不管是1d还是2d, 单个卷积核本质上还是一个线性操作, 需要结合非线性激活才能赋予其非线性能力;
(2)网络同质化严重,
(3)网络过于复杂, 参数量太大, 不利于部署 (CNN实际部署需要涉及轻量级的网络)。
ONN
ONN通过引入运算符集库大大增加了其非线性能力, 然而搜索最有的运算符集合非常耗时,并且运算符集库的选择很大程度上决定了性能上限。
SelfONN
SelfONN是对ONN的升级和改进,其核心思想是基于泰勒展开对函数进行近似, 这样一来就不需要预先定义运算符集库并且也避免了搜索最佳运算符集合的代价。
对于任何一个网络层,本质上是在学习一个函数f, 其泰勒展开如下:
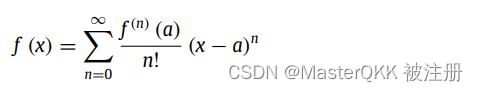
其Q阶的泰勒展开作为f的近似如下,
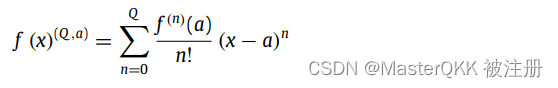
上述近似只有在a的领域内采有效, 即在 [ α − λ , α + λ ] [\alpha -\lambda, \alpha+\lambda] [α−λ,α+λ]内有效, 特别的,当a=0,并且采用tanh激活函数时,该区间为[-1, 1]. 这意味着输入的范围应该位于该区间内。
下面介绍改Q阶近似如何与SelfONN layer关联起来,
如上公式所示,该近似需要用到x的1~Q阶指数变换, 将其作为Operator sets, 然后将每一项前与梯度有关的系数作为网络科学系的权重,
这样一来,第l层的第k个neuro的操作可以用如下公式表示,
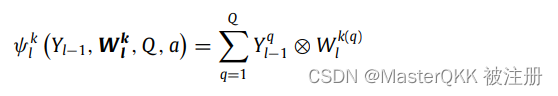
其中
W
l
k
W^{k}_{l}
Wlk的尺寸为[M, N, Q],
该操作关于输入和权重的梯度计算如下,
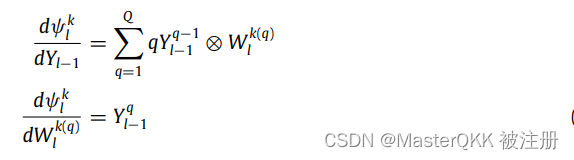
CNN, ONN, SelfONN对比
对于单通道的输入, 这三个操作的过程如下,

SelfONN与CNN的关系
可以看到Q实际上决定近似程度, 特别的, 当Q=1并且最终的聚合函数 ϕ = s u m \phi=sum ϕ=sum时, SelfONN layer完全退化为了CNN, 从这个角度来说, SelfONN可以看作是CNN的更加General的形式。
总结
SelfONN的简介到此为止, 对其相关理论以及在各个领域/任务感兴趣的可以查找相关论文, 主要都是MONCEF GABBOUJ团队写的。
References
- Self-organized operational neural networks for severe image
restoration problems, Neural Networks, 2021; - Self-organized Operational Neural Networks with Generative Neurons, Neural Networks, 2021;
- Operational Neural Networks, ArXIv, 2019.





![[保研/考研机试] KY188 哈夫曼树 北京邮电大学复试上机题 C++实现](https://img-blog.csdnimg.cn/53102df5263f4a37b5af1779a841df2f.png)