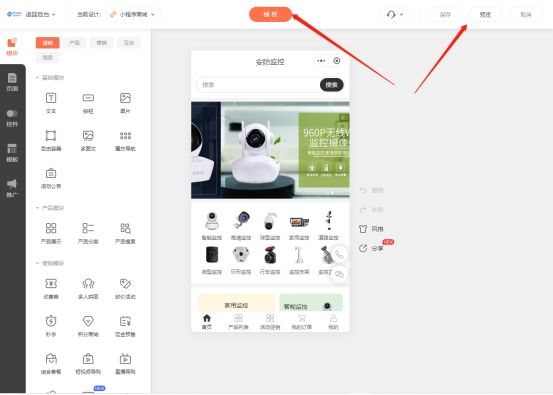
高斯分布
- 一、概念
- 二、详解和例子说明
- 三、判断数据是否服从高斯分布
- 四、高斯分布实际应用
一、概念
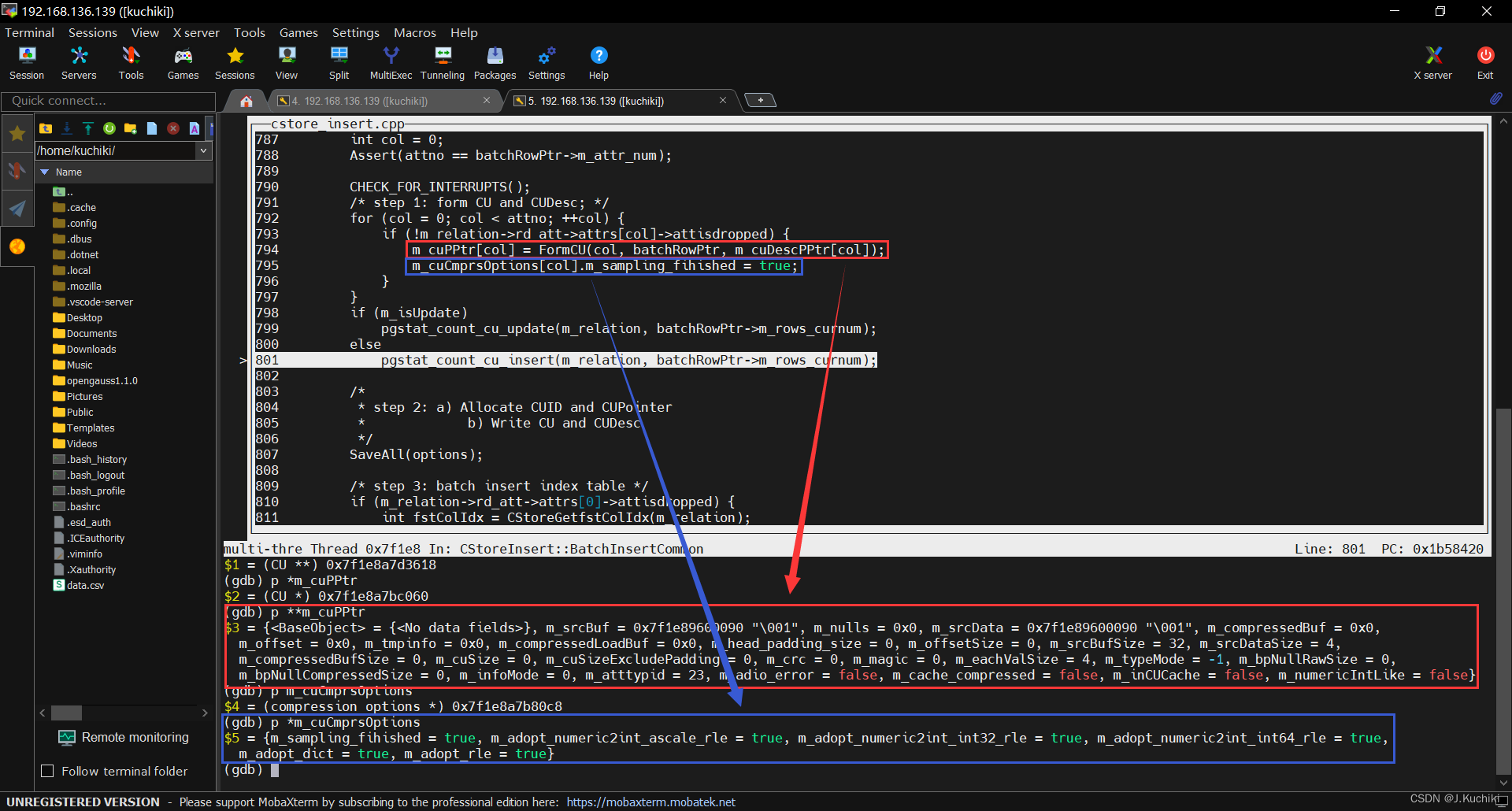
定义:随机变量X服从一个数学期望
μ
\mu
μ、方差为
σ
\sigma
σ的高斯分布,又名正态分布。当μ = 0,σ = 1时的正态分布是标准正态分布。
高斯分布概率密度函数(正态随机变量概率密度函数):
f
(
x
)
=
1
2
π
σ
e
x
p
(
−
(
x
−
μ
)
2
2
σ
2
)
f(x)=\frac {1}{\sqrt{2π}\sigma}exp(-\frac{(x-\mu)^2}{2\sigma^2})
f(x)=2πσ1exp(−2σ2(x−μ)2)
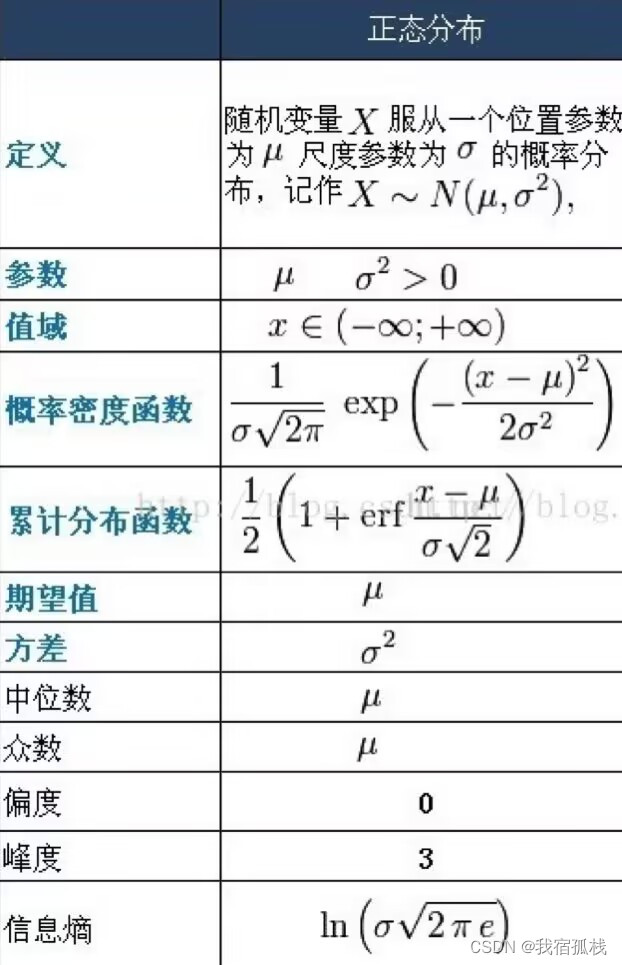
下图为高斯密度函数的函数曲线:
概率密度函数:y=f(x),x 是样本特性自变量,y 是 x 在这个样本特性上的数量比例。
exp:exp 指的是自然常数 e 的幂函数,即 e 的多少次幂的概念(e 是一个无理数,也就是无限不循环小数,e≈2.71828…)。比如
e
x
p
(
3
)
=
e
3
exp(3)=e^3
exp(3)=e3
这个函数的峰值在
x
=
μ
x=\mu
x=μ的位置,此时对应的函数值 y 为:
1
2
π
σ
\frac {1}{\sqrt{2π}\sigma}
2πσ1。
这里样本数量的计算用的是定积分的定义,即整个函数曲线在其下方围住的与 y=0(x 轴)所围成的面积占比。它在 x = μ x=\mu x=μ 左右两侧的函数是对称的:
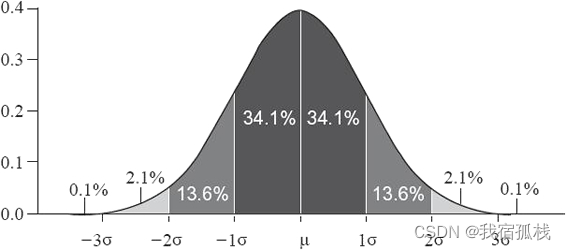
- x 在 μ-σ 和 μ+σ 之间的样本数量占到整个样本数量的 68.2%;
- x 在 μ-2σ 和 μ+2σ 之间的样本数量占到整个样本数量的 95.4%;
- x 在 μ-3σ 和 μ+3σ 之间的样本数量占到整个样本数量的99.6%;
二、详解和例子说明
高斯分布作为分布特性的一种,首先是用来描述统计对象的,如果统计对象的分布特性符合高斯分布,那么所有针对高斯分布的定理和“经验值”就能够直接套用。而高斯分布本身在自然界的应用是非常广泛的,用一句话解释高斯分布所表现的分布特点就是“一般般的很多,极端的很少”。
这里举一个具体的例子,假如对某一地区的男性身高做了一个随机抽样,一共 1000 人,结果发现他们的身高是一个 μ=175cm 的高斯分布,σ=10cm。那么首先,这样一个描述就已经能够清晰地说明这个抽样检查的结果了,而以下结论也就随之成立(如下曲线图)。
- 身高 165~175cm 的人(大约)有 341 名。
- 身高 175~185cm 的人(大约)有 341 名。
- 身高 155~165cm 的人(大约)有 136 名。
- 身高 185~195cm 的人(大约)有 136 名。
- 身高 145~155cm 的人(大约)有 21 名。
- 身高 195~205cm 的人(大约)有 21 名。
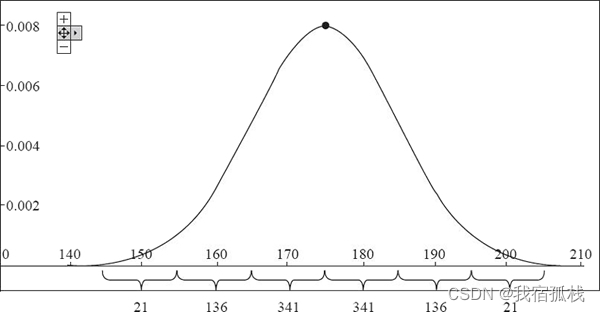
这些数量基本已经涵盖了统计总人数的 99.6 %。需要注意的是,根据统计的情况在不同的条件下 μ 和 σ 的值可能会不同:
- μ 较大,则整个函数图像的中轴向右挪动比较多。
- μ 较小,则函数图像的中轴向左挪动比较多。
- σ 较大,则整个曲线绵延比较长,整个坡度显得平缓。
- σ 较小,整个曲线窄而立陡。
符合高斯分布的其它例子:
智商分布:智慧一般的人很多,非常聪明的人较少,非常愚笨的人也较少(在一些大公司或者重点学校里虽然整体的聪明程度提高,但是还是存在这个小范围内的高斯分布,即 μ 比较偏右,而 σ 比较小)
收入分布:全社会范围内的收入,中档次收入的人比较多,特别贫穷和特别富裕的人较少,但是他们在地域上的分布和职业类别上的分布可能就不那么均匀了。
三、判断数据是否服从高斯分布
1、看直方图! 是不是看起来像钟形?
2、计算描述性汇总度量 - 平均值,中位数和模式是否相似?
3、2/3的观察值是否位于平均值的±标准差1内? 95%的观察值是否在平均值的±2标准差范围内?
四、高斯分布实际应用
首先刚才说过,如果在统计过程中发现一个样本呈现高斯分布的特性,只需要把样本总数量、μ 和 σ 表述出来,就已经能够形成一个完整的画面感了。这对人们描述对象是有很大帮助的。还有一个好处,就是我们发现了这样一个特性以后,在生产制造、商业等领域会有很多对应性的用法能够减少不必要的投入或损失。
例如,在设计一款服装后,S/M/L/XL 这些号码怎么设计比较合理呢?设计完了制造多少较合理呢?这时就可以在抽样后在高斯分布曲线上找到这些合适的点。既然 μ-σ 和 μ+σ 之间已经占 68.2%了,那么如果没有足够的预算或者精力,可以只先尝试做一个以 μ 为标准的板式,针对一部分人打板做市场推广。因为再做 μ-σ 和 μ+σ 这两个如此不同的板式,打板成本将会再提高 2 倍,但是增益仅有不到 50%(这从概率密度函数上就可以看出来)。这其实就是一种针对市场迎合的分析和尝试,即优先做那些受众情况最一般、人数最集中的部分。