来源：力扣（LeetCode）

描述：

给你一个无向图，无向图由整数 n ，表示图中节点的数目，和 edges 组成，其中 edges[i] = [ui, vi] 表示 ui 和 vi 之间有一条无向边。同时给你一个代表查询的整数数组 queries 。

第 j 个查询的答案是满足如下条件的点对 (a, b) 的数目：

• a < b
• cnt 是与 a 或者 b 相连的边的数目，且 cnt 严格大于 queries[j] 。

请你返回一个数组 answers ，其中 answers.length == queries.length 且 answers[j] 是第 j 个查询的答案。

请注意，图中可能会有 重复边 。

示例 1：

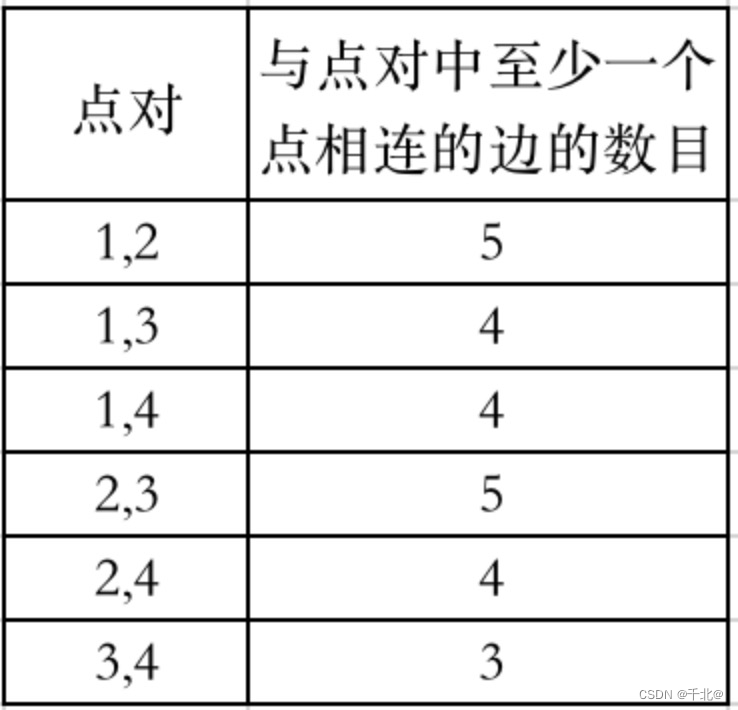
输入：n = 4, edges = [[1,2],[2,4],[1,3],[2,3],[2,1]], queries = [2,3]
输出：[6,5]
解释：每个点对中，与至少一个点相连的边的数目如上图所示。

示例 2：

输入：n = 5, edges = [[1,5],[1,5],[3,4],[2,5],[1,3],[5,1],[2,3],[2,5]], queries = [1,2,3,4,5]
输出：[10,10,9,8,6]

提示：

• 2 <= n <= 2 * 10⁴
• 1 <= edges.length <= 10⁵
• 1 <= ui, vi <= n
• ui != vi
• 1 <= queries.length <= 20
• 0 <= queries[j] < edges.length

方法一: 二分查找

思路与算法

根据题意可知，每次查询时给定的 queries[j]，需要统计满足如下条件的点对 (a, b) 的数目：

• a < b ；
• 对于每次查询 queries[j]，与节点 a 或者节点 b 相连的边的数目之和严格大于 queries[j]。

设节点 x 的度为 degree[x]，我们知道与节点 a 相连的边的数目即为 a 的度数 degree[a]，与节点 b 相连的边的数目即节点 b 的度数 degree[b]，如果此时节点 a 与节点 b 之间不存在相连的边，则此时与点对 (a, b) 相连的边的数目即为 degree[a] + degree[b]。

• 需要注意的与节点 a 或者节点 b 相连的边的数目之和则不一定等于 a 的度数与 b 的度数之和，这是因为 a 与 b 之间可能存在相连的边，假设 a 与 b 之间相连边的数目为 cnt(a, b)，则此时与点对 (a, b) 相连的边的数目即为 degree[a] + degree[b] − cnt(a, b)，这是由于 cnt(a, b) 被计算了两次。

根据以上分析，对于每次查询时，假设当前给定边的查询值为 queries[i]，此时最直接的做法是使用双层循环遍历所有的点对 (a, b)，然后找到所有满足的点对即可，但此时时间复杂度为 O(n²)，按照题目给定的数量会超时。假设给定点 a，则此时点对的另一节点 b 的度数应该大于 queries[i] − degree[b]，因此可以考虑利用二分查找在 O(log⁡n) 的时间复杂度找到满足要求的点 b 的数目，同时还需处理 a, b 存在共边的问题，可以分两步进行：

• 此时首先找到所有满足 degree[a] + degree[b] > queries[i] 的点对数量。二分查找的思路非常简单，假设当前的点 a 的度为 degree[a]，则利用二分查找在数组中查找当前度数大于 queries[i] − degree[a] 的节点数量，为了方便计算，需要将 degree 按照从小到大的顺序进行排列即可，利用二分查找大于 queries[i] - degree[a] 的索引为 j，则此时可以与 a 构成符合要求的节点数量为 n − j，按照上述方法找到所有满足要求的点对数量为 total；
• 其次需要处理 (a, b) 存在共边的问题，即减去重复计算的部分。我们用哈希存储表 cnt 存储不同边的数量，由于所有的边均为无向边，因此边 ab 与 边 ba 为同样的边，此时为了方便处理可以将边 ab 映射到一个整数 a × n + b, (a < b)。遍历所有的边 ab，此时点对 (a,b) 中重复计算边的数目即为 cnt(a, b) 。此时如果点对 (a, b) 减去重复部分后相连边的数目小于等于 queries[i] ，则认为该点对不满足要求，即从当点对 (a, b) 满足： degree[a] + degree[b] − cnt(a, b) ≤ queries[i] total 的记数减 1 ，最终得到的 total 即可本次的查询结果；

根据以上方法找到每次查询的点对数量，并返回结果即可。

代码：

class Solution {
public:
    vector<int> countPairs(int n, vector<vector<int>>& edges, vector<int>& queries) {
        vector<int> degree(n);
        unordered_map<int, int> cnt;
        for (auto edge : edges) {
            int x = edge[0] - 1, y = edge[1] - 1;
            if (x > y) {
                swap(x, y);
            }
            degree[x]++;
            degree[y]++;
            cnt[x * n + y]++;
        }

        vector<int> arr = degree;
        vector<int> ans;
        sort(arr.begin(), arr.end());
        for (int bound : queries) {
            int total = 0;
            for (int i = 0; i < n; i++) {
                int j = upper_bound(arr.begin() + i + 1, arr.end(), bound - arr[i]) - arr.begin();
                total += n - j;
            }
            for (auto &[val, freq] : cnt) {
                int x = val / n;
                int y = val % n;
                if (degree[x] + degree[y] > bound && degree[x] + degree[y] - freq <= bound) {
                    total--;
                }
            }
            ans.emplace_back(total);
        }

        return ans;
    }
};

时间 824ms 击败 43.75%使用 C++ 的用户
内存 186.11MB 击败 42.19%使用 C++ 的用户
复杂度分析

• 时间复杂度：O(q×(nlog⁡n+m)) ，其中 q 表示查询数组 queries 的铲毒，n 表示给定的节点的数目，m 表示边 edges 的长度。对所有的点的度数排序时需要的时间复杂度为 O(nlogn)，每次查询时需要二分查找找到所有符合要求的点对，并同时遍历所有的边，需要的时间为 O(nlogn+m)，一共有 q 次查询，因此总的时间复杂度为 O(nlog⁡n+q×(nlog⁡n+m)) = O(q×(nlog⁡n+m))。
• 空间复杂度：O(n+m) ，其中 n 表示给定的节点的数目，m 表示边 edges 的数目。我们需要存储每个点的度数，需要的空间为 O(n) ，还需统计每条边出现的次数，需要的空间为 O(m)，因此总的空间复杂度为 O(n+m)。

方法二: 双指针

思路与算法

方法二的解法思路跟方法一基本一致，唯一需要特殊处理的是找满足 degree[a] + degree[b] > bound 的点对时可以利用双指针来处理：

假设当前从小到大第 i 节点 a 的度为 degree[a] ，我们从后往前找到第一个满足小于等于 bound − degree[a] 的节点索引为 j ，则此时 b ∈ [j + 1, n − 1] 均满足 degree[a] + degree[b] > queries[i] ，则此时与 a 构成满足要求的节点的数目位 n − 1 − j ，为了防止重复计算，此时只取大于 i 且大于 j 的索引，则此时 b ∈ [max⁡(i + 1, j + 1), n − 1] 区间内的索引即可；

代码 ：

class Solution {
public:
    vector<int> countPairs(int n, vector<vector<int>>& edges, vector<int>& queries) {
        vector<int> degree(n);
        unordered_map<int, int> cnt;
        for (auto edge : edges) {
            int x = edge[0] - 1, y = edge[1] - 1;
            if (x > y) {
                swap(x, y);
            }
            degree[x]++;
            degree[y]++;
            cnt[x * n + y]++;
        }

        vector<int> arr = degree;
        vector<int> ans;
        sort(arr.begin(), arr.end());
        for (int bound : queries) {
            int total = 0;
            for (int i = 0, j = n - 1; i < n; i++) {
                while (j > i && arr[i] + arr[j] > bound) {
                    j--;
                }
                total += n - 1 - max(i, j);
            }
            for (auto &[val, freq] : cnt) {
                int x = val / n;
                int y = val % n;
                if (degree[x] + degree[y] > bound && degree[x] + degree[y] - freq <= bound) {
                    total--;
                }
            }
            ans.emplace_back(total);
        }

        return ans;
    }
};

时间 696ms 击败 57.81%使用 C++ 的用户
内存 186.10MB 击败 42.19%使用 C++ 的用户
复杂度分析

• 时间复杂度：O(nlog⁡n+q×(n+m)) ，其中 q 表示查询数组 queries 的铲毒，n 表示给定的节点的数目，m 表示边 edges 的长度。对所有的点的度数排序时需要的时间复杂度为 O(nlog⁡n) ，每次查询时需要遍历所有点的度数，并同时遍历所有的边，需要的时间为 O(n+m) ，一共有 q 次查询，因此总的时间复杂度为 O(nlog⁡n+q×(n+m)) 。
• 空间复杂度：O(n+m) ，其中 n 表示给定的节点的数目，m 表示边 edges 的数目。我们需要存储每个点的度数，需要的空间为 O(n) ，还需统计每条边出现的次数，需要的空间为 O(m)，因此总的空间复杂度为 O(n+m)。
  author：力扣官方题解