取模运算符在数组下标的应用

news2025/2/26 20:10:19

什么是取模运算符%？

定义：

a mod b，设a、b属于正整数且b>0，如果q、r属于正整数满足a=q*b+r，且0≤r<b，则定义：

a mod b = r

注意：取模运算符两侧的除数和被除数都是整数，不能是小数。如果你将小数带入运算，编译器可能会出现以下报错，例如 1% 0.5 ：

想要很好地利用%，我们就先要了解一下取模运算符的运算性质：

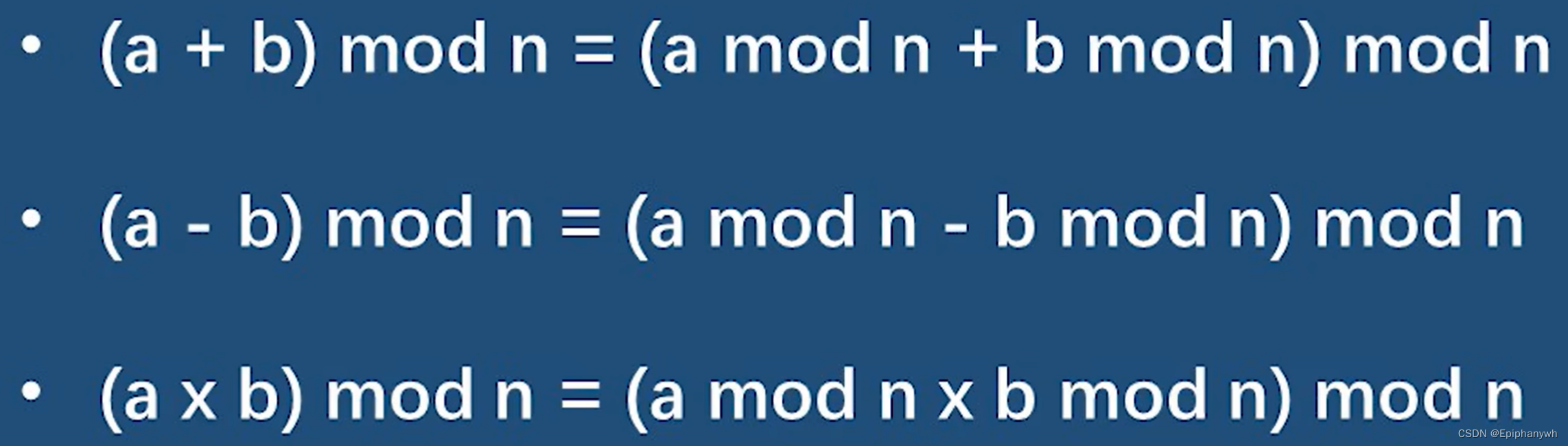
模运算的应用

1. 将下标控制在一定的范围

根据取模运算的运算性质，模运算结果的范围是 0 ~ (除数-1)。反过来就是，如果你想将数据控制在 0 ~ x ，你就可以 %（x+1）。

2. 利用当前下标获取前一个元素

我们想要获取当前下标的前一个时，可能会出现这两种种情况：当前下标是第一个下标时，那么它对应的前一个数据就是下标为末尾的元素；其他情况下，可以直接用当前下标-1来获得前一个元素。例如，当前下标为0时，它对应的前一个元素就是下标为7的元素；当前下标为2时，它对应的前一个元素就是下标为2-1=1的元素

那么我们如何利用%来实现这一个过程呢？

这里我先给出答案在做出解释：

i = （x+size）%（size+1），这里 i 代表最终下标，x代表当前下标，size代表数组的最后一个下标（注意不是数组长度）；

分析：

根据我们的需求，我们想要x经过%运算后能够变为x-1，并且在特殊情况下，x=0可以变成x等于最后一个下标，再根据取模运算的性质，（x+size）%（size+1）可以写成（（x-1）+size+1）%（size+1）--> （x-1）%（size+1）+（size+1）%（size+1），因为（x-1）一定小于（size+1），所以前半部分的运算结果就是（x-1），后半部分运算结果为0，最终结果就是（x-1）。

其实，主要思想就是将 x 配凑成 x-1，那么可能会有疑惑：为什么不把x直接减一进行运算呢？

事实上，这里有一点需要注意：取模运算 mod 是可以满足的，我们使用%运算主要想应对的就是下标为零的情况，当下标为零时，直接减一，会变成 -1 mod（size+1），这里就涉及负数作为被除数的运算：

在数学中，余数通常定义为非负整数，所以最终答案是1（运算-13 = （-2）*7 + 1），我们会发现这样不就满足我们的需求了吗，例如：（0-1）%（4+1）= 4 （ -1 = (-1)*(4+1) + 4）。

但是，在编程中，通常取模运算（%）的结果会保持符号与被除数一致。这是因为在计算机中，% 运算符会根据被除数的符号来确定余数的符号。所以如果你在编译器上运算这个式子，答案会是-6，因为编译器在运算时会先将负号去掉进行计算：13%7=6，最终的结果会根据被除数的符号确定，因为被除数（-13）是负数，所以最终的答案是-6.

所以，我们不能通过直接减一达到我们想要的效果，而是通过加上一个size来配凑。