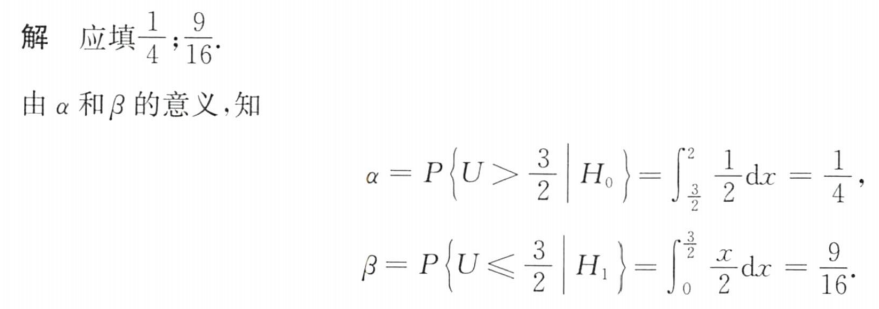文章目录
- Ch7. 参数估计
- 7.1 点估计
- 1.矩估计
- 2.最大似然估计
- (1)离散型
- (2)连续型
- 7.2 评价估计量优良性的标准
- (1)无偏性 (无偏估计)
- (2)有效性
- (3)一致性
- 7.3 区间估计
- 1.置信区间、置信度
- 2.求μ的置信区间
- Ch8. 假设检验
- 1.拒绝域α、接受域1-α、H₀原假设、H₁备择假设
- 2.双边检验、单边检验
- 3.第一类错误、第二类错误
Ch7. 参数估计
7.1 点估计
1.矩估计
p i ( θ ) p_i(θ) pi(θ)、 f ( x i , θ ) f(x_i,θ) f(xi,θ),用矩估计法来估计未知参数θ
{ X ˉ = E ( X ) 1 n ∑ i = 1 n X i 2 = E ( X 2 ) \left\{\begin{aligned} \bar{X} = & E(X) \\ \dfrac{1}{n}\sum\limits_{i=1}^nX_i^2 = & E(X^2) \end{aligned}\right. ⎩ ⎨ ⎧Xˉ=n1i=1∑nXi2=E(X)E(X2)
注意:
1.矩估计量:大写
矩估计值:小写
2.离散型和连续型随机变量
求矩估计的区别,只在于求期望的方法不一样。
而求最大似然估计,则是似然函数的求法不一样。
例题1:23李林六套卷(三)22.(2)
若θ为未知参数,利用总体Z的样本值
−
2
,
0
,
0
,
0
,
2
,
2
-2,0,0,0,2,2
−2,0,0,0,2,2求
θ
θ
θ的矩估计值。且Z的分布律为
| Z Z Z | − 2 -2 −2 | 0 0 0 | 2 2 2 |
|---|---|---|---|
| P k P_k Pk | θ θ θ | 1 − 2 θ 1-2θ 1−2θ | θ θ θ |
答案:

例题2:09年23(1)

分析:
①矩估计,求期望
②最大似然估计,求似然函数L(θ),取对数lnL(θ),令导数为0即令
d
l
n
L
(
θ
)
d
θ
=
0
\frac{\rm dlnL(θ)}{\rm dθ}=0
dθdlnL(θ)=0
答案:
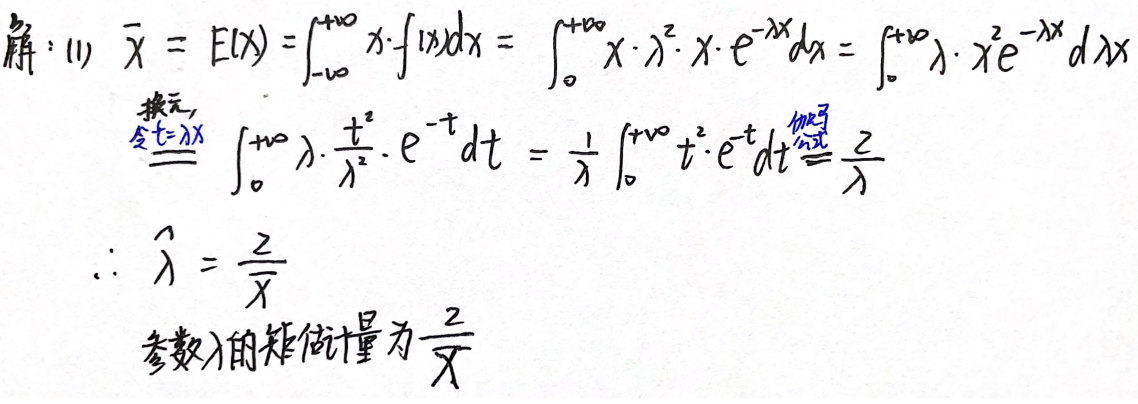
例题3:13年23.(难度:易)

2.最大似然估计
最大似然估计求的是,θ为多少时,使得L(θ)最大
(1)离散型
求离散型随机变量的最大似然估计量:
离散型的似然函数
L
(
θ
)
=
∏
i
=
1
n
p
(
x
i
,
θ
)
L(θ)=\prod\limits_{i=1}^n{p(x_i,θ)}
L(θ)=i=1∏np(xi,θ)
=
p
(
x
1
,
θ
)
⋅
p
(
x
2
,
θ
)
⋅
.
.
.
⋅
p
(
x
n
,
θ
)
=p(x_1,θ)·p(x_2,θ)·...·p(x_n,θ)
=p(x1,θ)⋅p(x2,θ)⋅...⋅p(xn,θ)
x 1 , x 2 , . . . , x n x_1,x_2,...,x_n x1,x2,...,xn为离散型样本值,根据样本来确定是哪些概率相乘。
(2)连续型
求连续型随机变量的最大似然估计量,连续型的似然函数L(θ)
L
(
θ
)
=
L
(
x
1
,
x
2
,
.
.
.
,
x
n
;
θ
)
=
∏
i
=
1
n
f
(
x
i
;
θ
)
(
x
i
>
0
,
i
=
1
,
2
,
.
.
.
n
)
L(θ) = L(x_1,x_2,...,x_n;θ) = \prod_{i=1}^n f(x_i;θ) \qquad (x_i>0,i=1,2,...n)
L(θ)=L(x1,x2,...,xn;θ)=i=1∏nf(xi;θ)(xi>0,i=1,2,...n)
1.求最大似然估计量/值 的步骤:
①求似然函数 L(θ) (xi>0/θ,i=1,2,…n)
②取对数,求 lnL(θ)
③令
d
l
n
L
(
θ
)
d
θ
=
0
\dfrac{\rm d lnL(θ)}{\rm dθ} = 0
dθdlnL(θ)=0,求出
θ
^
\hat{θ}
θ^
④最大似然估计值为xi,最大似然估计量为Xi
2.求导不为0,>0为增函数,<0为减函数。且一定有限制。
若
d
l
n
L
(
θ
)
d
θ
≠
0
\dfrac{\rm d lnL(θ)}{\rm dθ} ≠ 0
dθdlnL(θ)=0
{
d
l
n
L
(
θ
)
d
θ
>
0
,
L
(
θ
)
为增函数,
θ
应取最大值
d
l
n
L
(
θ
)
d
θ
<
0
,
L
(
θ
)
为减函数,
θ
应取最小值
\left\{\begin{aligned} \dfrac{\rm d lnL(θ)}{\rm dθ} > 0,&L(θ)为增函数,θ应取最大值\\ \dfrac{\rm d lnL(θ)}{\rm dθ} < 0,&L(θ)为减函数,θ应取最小值 \end{aligned}\right.
⎩
⎨
⎧dθdlnL(θ)>0,dθdlnL(θ)<0,L(θ)为增函数,θ应取最大值L(θ)为减函数,θ应取最小值
见2000年21.
3.均匀分布的最大似然估计
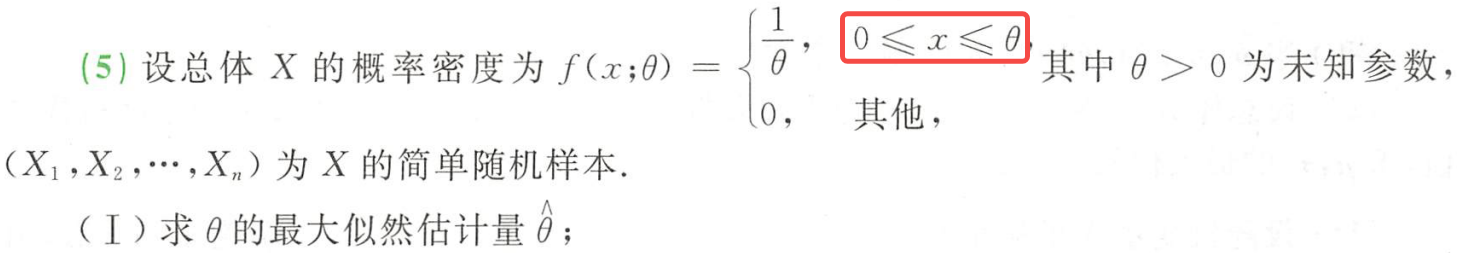

例题1:2002年20. 离散型的参数估计
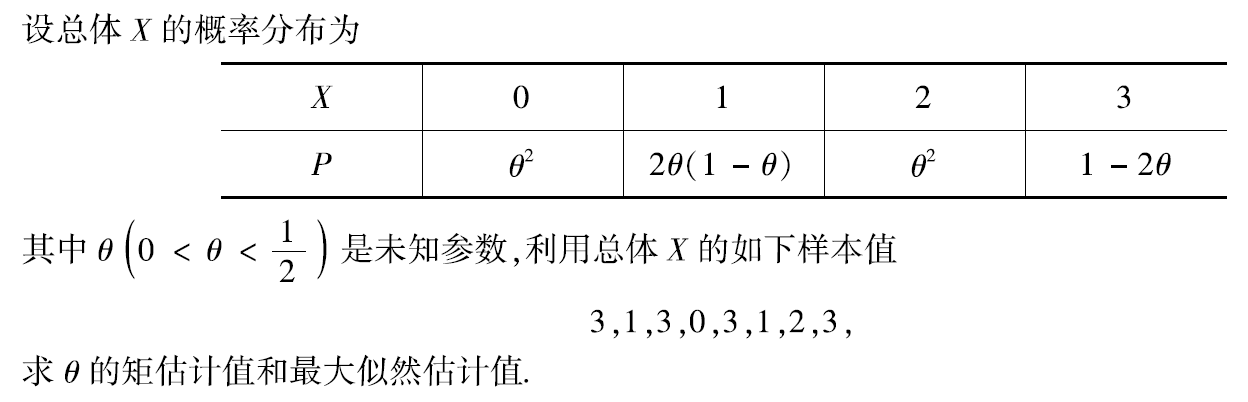
答案:

例题2:2000年21.
d
l
n
L
(
θ
)
d
θ
≠
0
\dfrac{\rm d lnL(θ)}{\rm dθ} ≠ 0
dθdlnL(θ)=0
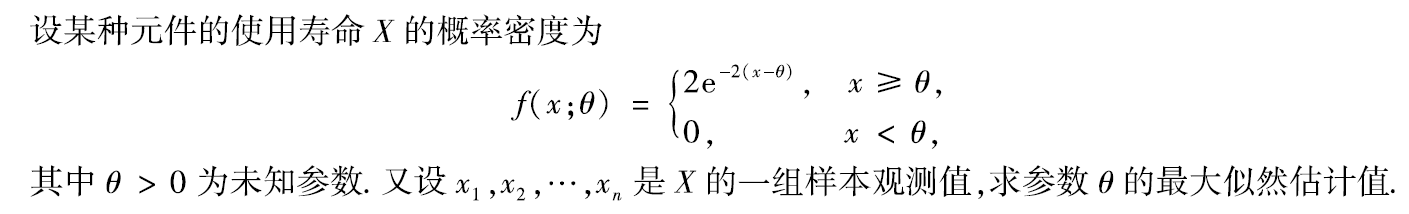
分析:
d
l
n
L
(
θ
)
d
θ
=
2
n
>
0
\frac{\rm d lnL(θ)}{\rm dθ} =2n >0
dθdlnL(θ)=2n>0,∴L(θ)为关于θ的增函数,θ应取最大值
∴θ的最大似然估计值为
θ
^
=
m
i
n
{
x
1
,
x
2
,
.
.
.
,
x
n
}
\hat{θ}=min\{x_1,x_2,...,x_n\}
θ^=min{x1,x2,...,xn}
例题3:19年23(2)

分析:
求σ2的最大似然函数:
①求似然函数L(σ2)
②取对数,lnL(σ2)
③令
d
l
n
L
(
σ
2
)
d
σ
2
=
0
\frac{\rm d lnL(σ^2)}{\rm dσ^2} = 0
dσ2dlnL(σ2)=0
答案:
σ2的最大似然估计值为
σ
^
2
=
1
n
∑
i
=
1
n
(
x
i
−
μ
)
2
\hat{σ}^2=\dfrac{1}{n}\sum\limits_{i=1}^n(x_i-μ)^2
σ^2=n1i=1∑n(xi−μ)2
σ2的最大似然估计量为
σ
^
2
=
1
n
∑
i
=
1
n
(
X
i
−
μ
)
2
\hat{σ}^2=\dfrac{1}{n}\sum\limits_{i=1}^n(X_i-μ)^2
σ^2=n1i=1∑n(Xi−μ)2
例题3:18年23(2)
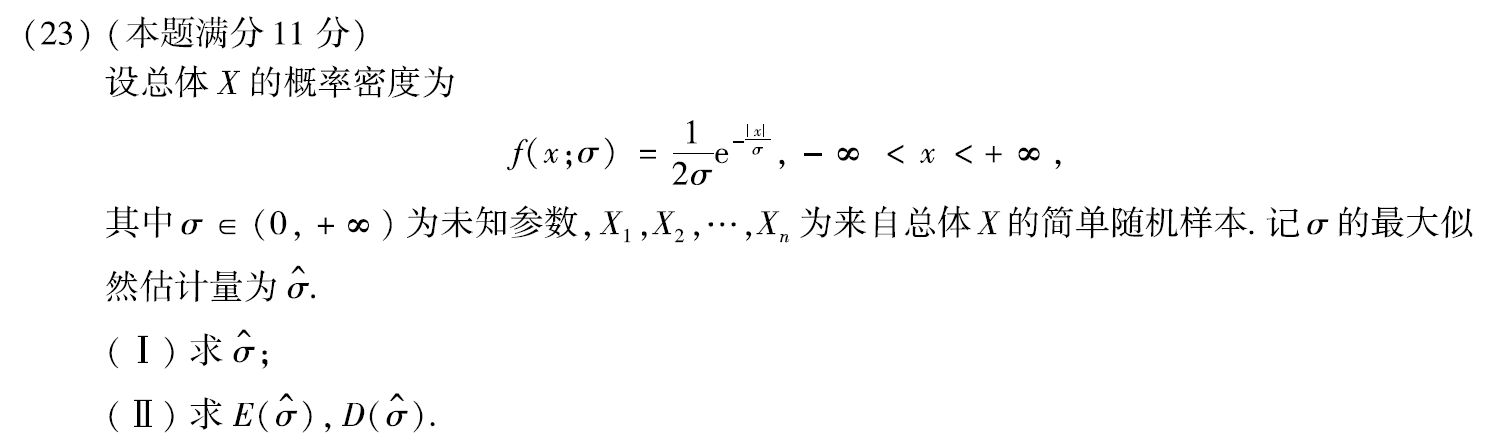
例题5:09年23(2)
习题1:23李林四(三)16.
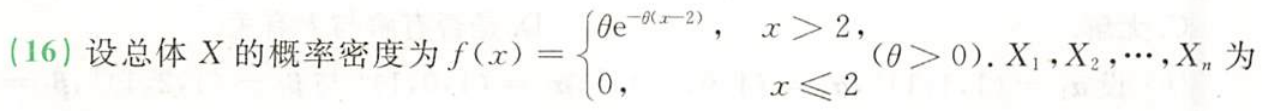
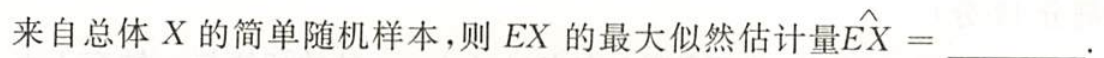
分析:
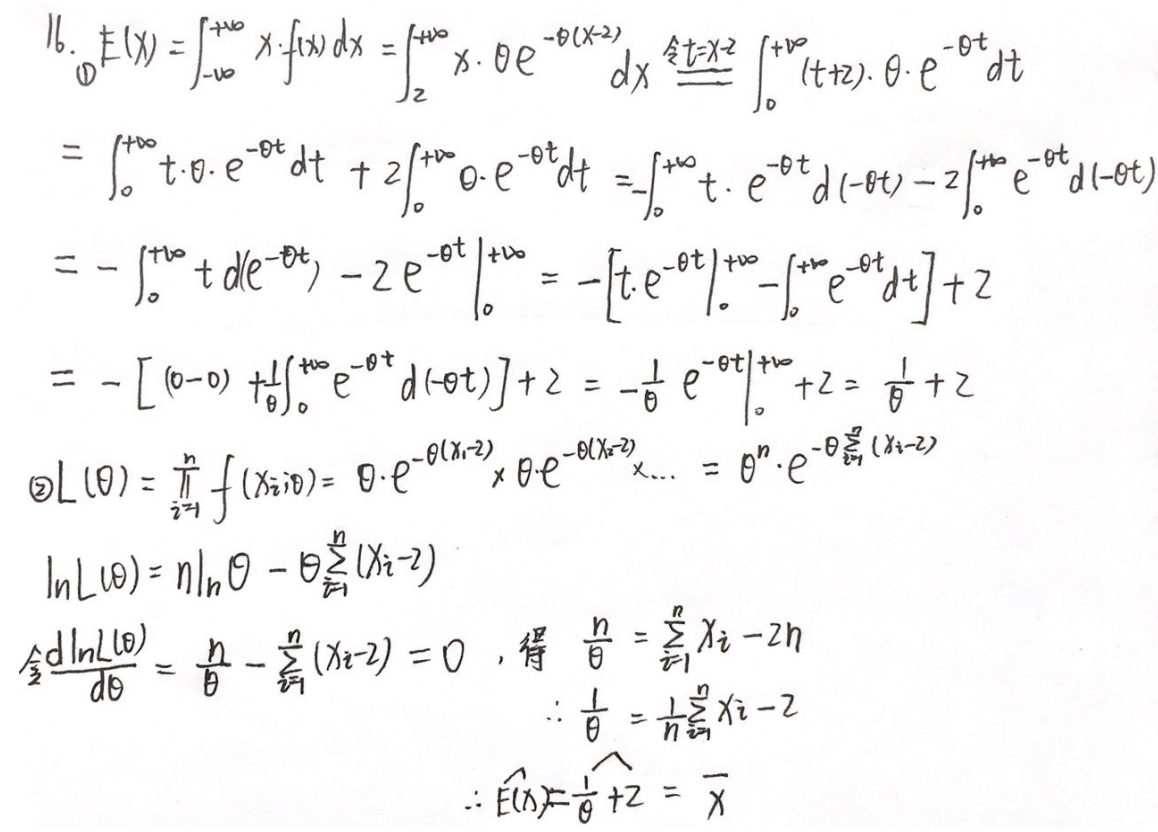
答案:
X
ˉ
\bar{X}
Xˉ
习题2:23李林四(二)16.
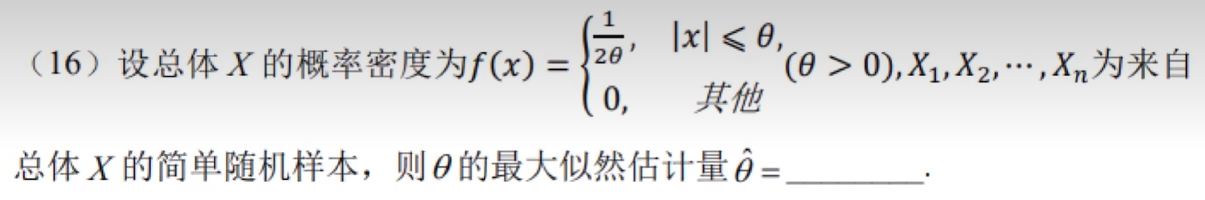
分析:∵|x|≤θ ∴θ的最大似然估计量为 θ ^ \hat{θ} θ^=max{|X₁|,|X₂|,…,|Xn|}
答案:max{|X₁|,|X₂|,…,|Xn|}
习题3:23李林六套卷(六)16. 二维随机变量求θ的最大似然估计

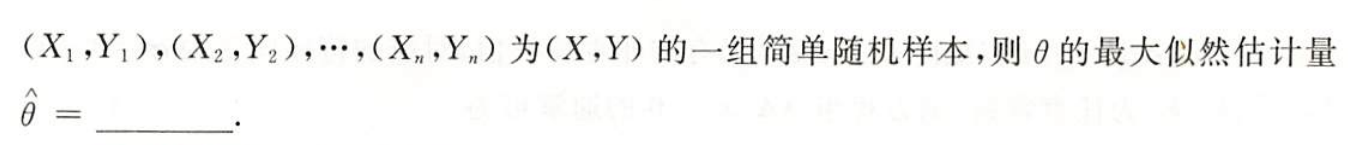
分析:

答案: 1 2 n ∑ i = 1 n ( X i + Y i ) \dfrac{1}{2n}\sum\limits_{i=1}^n(X_i+Y_i) 2n1i=1∑n(Xi+Yi)
习题4:22年22. 两个随机变量,求最大似然估计量

答案:

7.2 评价估计量优良性的标准
(1)无偏性 (无偏估计)
若参数θ的估计量 θ ^ = θ ^ ( X 1 , X 2 , . . . , X n ) \hat{θ}=\hat{θ}(X_1,X_2,...,X_n) θ^=θ^(X1,X2,...,Xn)对一切n及θ∈I,有 E ( θ ^ ) = θ E(\hat{θ})=θ E(θ^)=θ,则称 θ ^ \hat{θ} θ^为 θ θ θ的无偏估计量
即若 θ ^ \hat{θ} θ^是θ的无偏估计量,则 E ( θ ^ ) = θ E(\hat{θ})=θ E(θ^)=θ
E ( X ˉ ) = μ = E ( X ) , E ( S 2 ) = σ 2 = D ( X ) E(\bar X)=μ=E(X),E(S^2)=σ²=D(X) E(Xˉ)=μ=E(X),E(S2)=σ2=D(X)
(2)有效性
有效性(最小方差性):都是无偏估计量的情况下,方差小的更有效

(3)一致性
一致性(相合性):
θ
^
→
P
θ
\hat{θ}\xrightarrow{P}θ
θ^Pθ,依概率收敛

例题1:14年14.

分析:
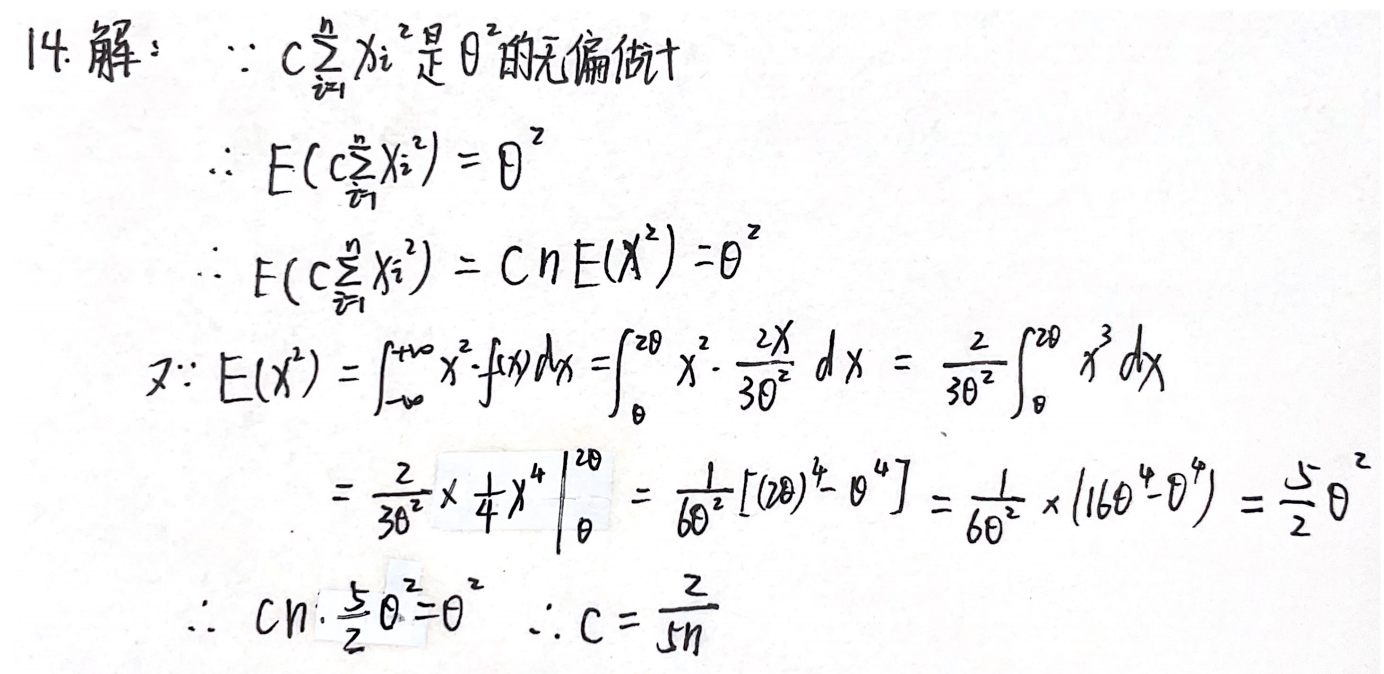
答案: 2 5 n \dfrac{2}{5n} 5n2
例题2:09年14. 无偏估计、二项分布的数字特征
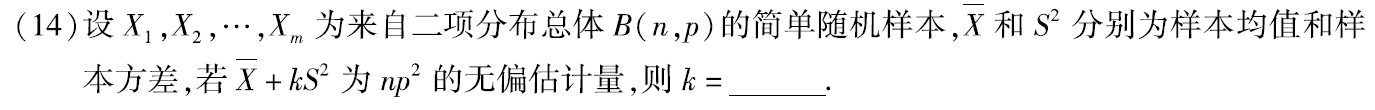
分析:
θ
^
\hat{θ}
θ^是θ的无偏估计量:
E
(
θ
^
)
=
θ
E(\hat{θ})=θ
E(θ^)=θ。
E
(
X
ˉ
)
=
μ
=
E
(
X
)
,
E
(
S
2
)
=
σ
2
=
D
(
X
)
E(\bar X)=μ=E(X),E(S^2)=σ²=D(X)
E(Xˉ)=μ=E(X),E(S2)=σ2=D(X)
则
E
(
X
ˉ
+
k
S
2
)
=
n
p
2
E(\bar X+kS^2)=np^2
E(Xˉ+kS2)=np2,即
E
(
X
ˉ
)
+
k
E
(
S
2
)
=
n
p
+
k
n
p
(
1
−
p
)
=
n
p
2
E(\bar X)+kE(S^2)=np+knp(1-p)=np^2
E(Xˉ)+kE(S2)=np+knp(1−p)=np2,化简得 k=-1
答案:-1
例题3:16年23(2)
例题4:12年23(3)
7.3 区间估计
1.置信区间、置信度
P { θ 1 < θ < θ 2 } = 1 − α P\{θ_1<θ<θ_2\}=1-α P{θ1<θ<θ2}=1−α
1 − α 1-α 1−α称为置信度(置信水平), α α α称为显著性水平
区间 ( θ 1 , θ 2 ) (θ_1,θ_2) (θ1,θ2)称为参数θ的置信度为1-α的置信区间。 θ 1 θ₁ θ1和 θ 2 θ₂ θ2分别称为置信度为 1 − α 1-α 1−α的置信区间的置信下限和置信上限;
2.求μ的置信区间
正态总体均值μ的置信区间(置信水平为1-α)
| 待估参数 | 其他参数 | 枢轴量的分布 | 置信区间 |
|---|---|---|---|
| μ | σ²已知 | Z = X ‾ − μ σ / n ∼ N ( 0 , 1 ) Z=\dfrac{\overline{X}-μ}{σ/\sqrt{n}}\sim N(0,1) Z=σ/nX−μ∼N(0,1) | ( X ‾ − Z α 2 σ n , X ‾ + Z α 2 σ n ) (\overline{X}-Z_{\frac{α}{2}}\dfrac{σ}{\sqrt{n}},\overline{X}+Z_{\frac{α}{2}}\dfrac{σ}{\sqrt{n}}) (X−Z2αnσ,X+Z2αnσ) |
| μ | σ²未知 | t = X ‾ − μ S / n ∼ t ( n − 1 ) t=\dfrac{\overline{X}-μ}{S/\sqrt{n}}\sim t(n-1) t=S/nX−μ∼t(n−1) | ( X ‾ − t α 2 ( n − 1 ) S n , X ‾ + t α 2 ( n − 1 ) S n ) (\overline{X}-t_{\frac{α}{2}}(n-1)\dfrac{S}{\sqrt{n}},\overline{X}+t_{\frac{α}{2}}(n-1)\dfrac{S}{\sqrt{n}}) (X−t2α(n−1)nS,X+t2α(n−1)nS) |
例题1:16年14. 置信区间、置信上限

分析:置信区间是以
X
ˉ
\bar{X}
Xˉ为中心对称的
X
ˉ
=
9.5
\bar{X}=9.5
Xˉ=9.5,
X
ˉ
\bar{X}
Xˉ到置信下限是1.3,则
X
ˉ
\bar{X}
Xˉ到置信上限也是1.3
答案: ( 8.2 , 10.8 ) (8.2,10.8) (8.2,10.8)
例题2:03年6.

分析:
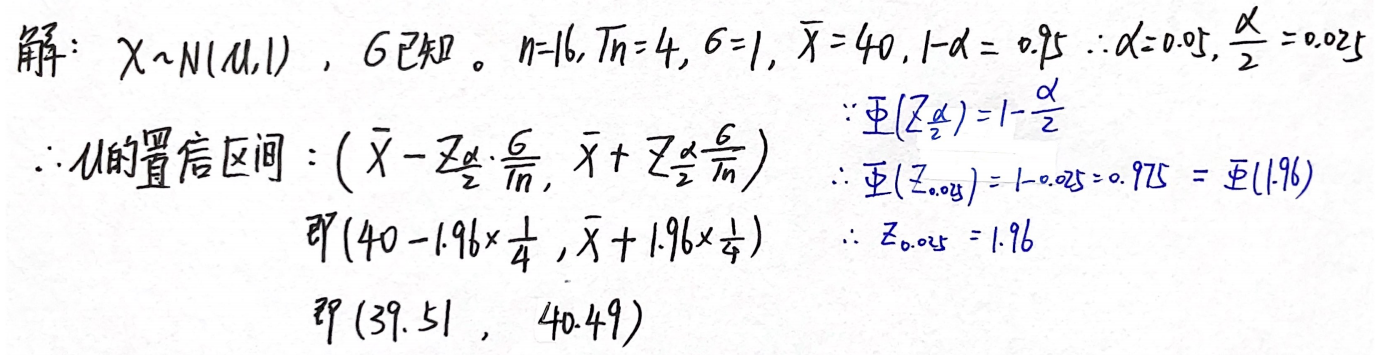
答案: ( 39.51 , 40.49 ) (39.51,40.49) (39.51,40.49)
Ch8. 假设检验
1.拒绝域α、接受域1-α、H₀原假设、H₁备择假设
检验水平(显著性水平)α,即为拒绝域面积。α越小,接受域越大。
例题1:18年8. 假设检验

分析:α为拒绝域。若拒绝,说明落在α内。若接受,说明落在α外。
答案:D
2.双边检验、单边检验
①接受域看H₀,拒绝域看H₁
②易错点:求未知数时,要代入原假设H₀中μ的值
μ
0
μ_0
μ0
(1)双边检验:
①H₀:μ=μ₀,H₁:μ≠μ₀
②α/2
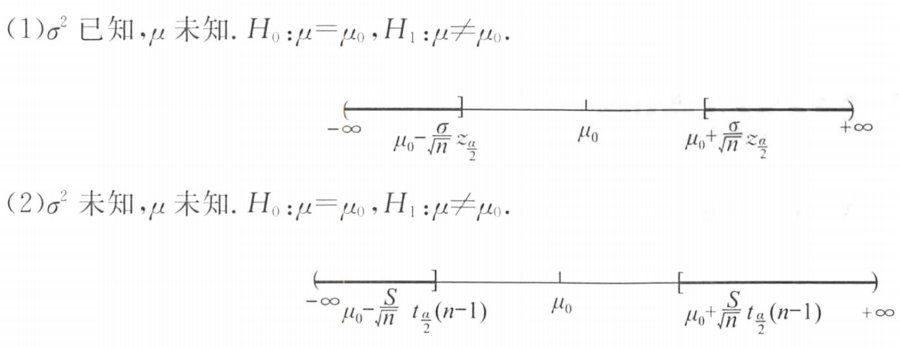
(2)单边检验:
①H₀:μ≥或≤μ₀,H₁:μ>或<μ₀
②α

例题1:

分析:

答案:求出拒绝域,得
x
ˉ
=
10
\bar{x}=10
xˉ=10落入拒绝域,拒绝原假设H₀
3.第一类错误、第二类错误
1.犯第一类错误(弃真):H₀为真的情况下,拒绝了H₀。
犯第一类错误的概率:
α
=
P
{
拒绝了
H
0
∣
H
0
为真
}
=
P
{
落在拒绝域
}
α=P\{拒绝了H_0|H_0为真 \}=P\{落在拒绝域\}
α=P{拒绝了H0∣H0为真}=P{落在拒绝域}
2.犯第二类错误(取伪):H₀为假的情况下,接受了H₀。
犯第二类错误的概率:
β
=
P
{
接受了
H
0
∣
H
0
为假
}
=
P
{
落在接受域
}
β=P\{接受了H_0|H_0为假\}=P\{落在接受域\}
β=P{接受了H0∣H0为假}=P{落在接受域}
常用性质:
①
P
{
x
>
a
}
=
1
−
P
{
x
≤
a
}
P\{x>a\}=1-P\{x≤a\}
P{x>a}=1−P{x≤a}
② Φ ( − x ) = 1 − Φ ( x ) Φ(-x)=1-Φ(x) Φ(−x)=1−Φ(x)
例题1:23李林六套卷(四)10. 犯第一类错误

分析:

答案:C
例题2:21年10. 犯第二类错误

分析:

答案:B
例题3:


分析:
犯第一类错误的概率α = P{H0为真,落在拒绝域}
犯第二类错误的概率β=P{H1为真,落在接受域}
答案: