E1. Unforgivable Curse (easy version)

Problem - 1800E1 - Codeforces

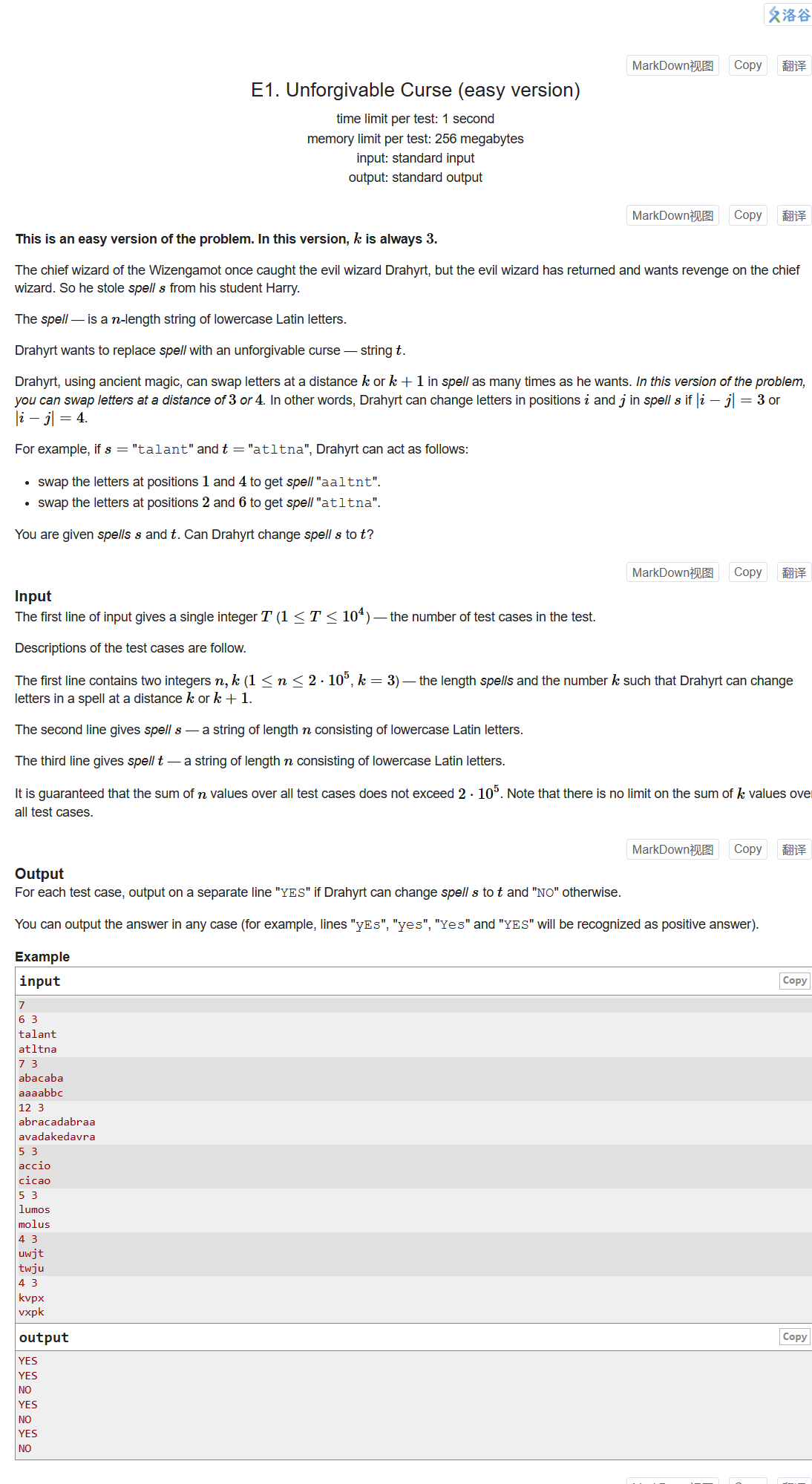
将s串转换成t串，每次能交换s串中下标绝对值差3或差4的字符
有点像bfs最小步数，但是字符串一共有$26^{2e5}$种，bfs肯定会RE
考虑一个无限长的s串，任意一个字符能走到字符串中的任意位置，向右走：+4-3或-3+4，向左走：+3-4或-4+3
考虑s串的长度，长度为多少时，才具有以上性质？
长度为1，2，3时，显然不行
长度为4，只有首尾两个字符能交换
长度为5，前两个字符于后两个字符能互相递达，只有中间的位置不可达
长度为6，任意字符可达任意位置

所以字符串长度大于等于6时，只要统计每个字符出现次数，判断是否相等即可
长度小于6时，用bfs最小步判断，s串是否能转换成t串即可

#include <iostream>
#include <string>
#include <queue>
#include <set>
using namespace std;

int T, n, k;
string s, t;
int dx[4] = { 3, 4, -3, -4 };

bool bfs()
{
    set<string> st;
    queue<string> q;
    q.push(s);
    while (q.size())
    {
        string str = q.front();
        q.pop();
        if (str == t) return true;
        for (int i = 0; i < n - 3; ++ i )
        {
            for (int j = 0; j < 4; ++ j )
            {
                int ni = i + dx[j];
                if (ni < n && ni >= 0) 
                {
                    swap(str[i], str[ni]);
                    if (!st.count(str)) 
                    {
                        st.insert(str);
                        q.push(str);
                    }
                    swap(str[i], str[ni]);
                }
            }
        }
    }
    
    return false;
}

int main()
{
    ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
    cin >> T;
    while ( T -- )
    {
        cin >> n >> k >> s >> t;
        if (n < 6) 
        {
            if (bfs()) puts("YES");
            else puts("NO");
        }
        else
        {
            int cnt[26] = {0}; bool flag = true;
            for (int i = 0 ; i < n; ++ i ) cnt[s[i] - 'a'] ++ ;
            for (int i = 0 ; i < n; ++ i ) 
                if ( -- cnt[t[i] - 'a'] < 0)  
                {
                    flag = false;
                    break;
                }
            if (flag) puts("YES");
            else puts("NO");
        }
    }
    return 0;
};

---

E2. Unforgivable Curse (hard version)

Problem - 1800E2 - Codeforces

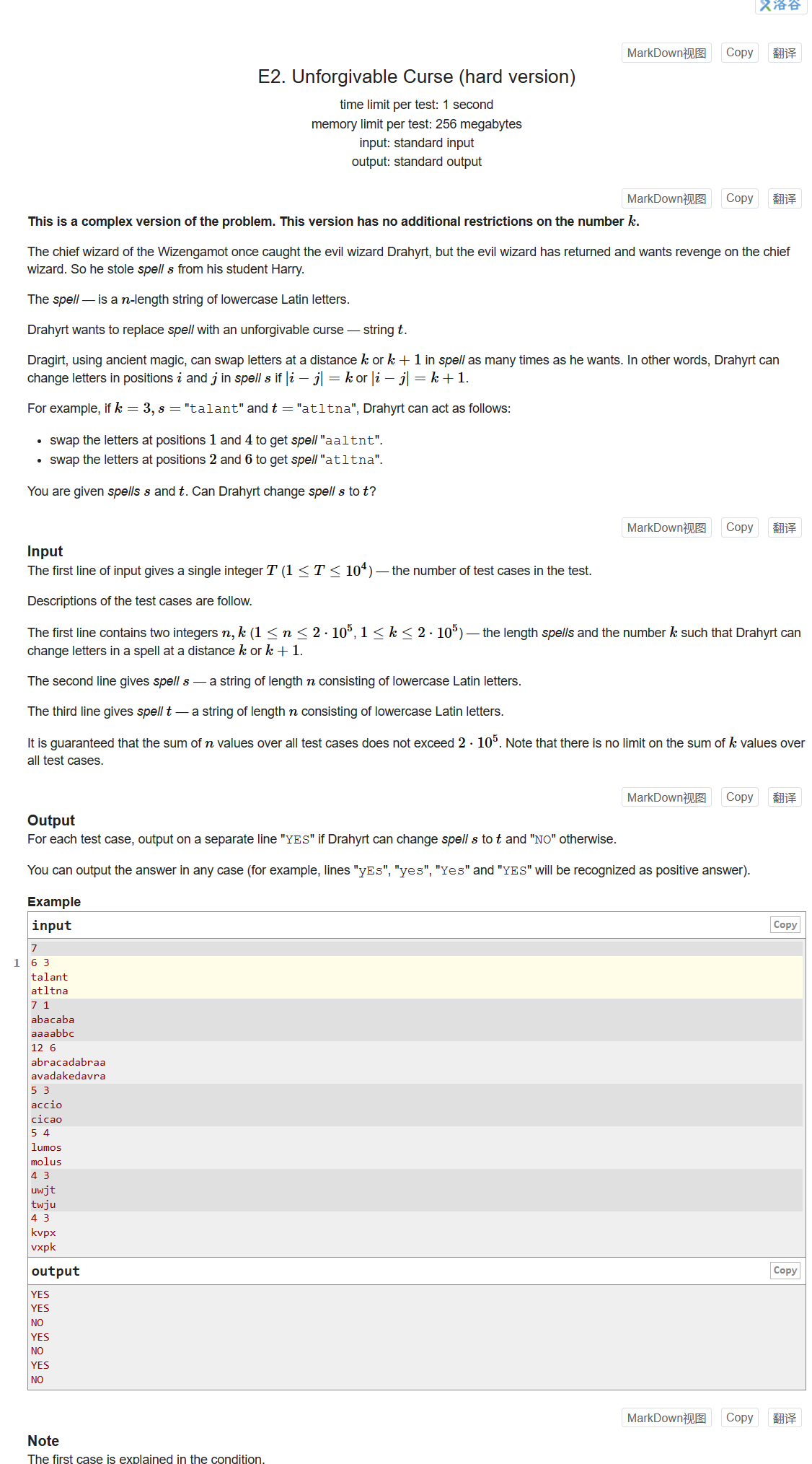
上一题的k总是3，这一题的k为$[1,2e5]$
考虑k会影响什么性质，上一题的k为3，只有长度大于等于6的字符串中的字符可以递达任意位置，所以我们只用比较每个字符出现的次数是否相等
推广一下，对于长度大于等于2 * \k的字符串利用以上性质判断
对于长度小于2 * \k的字符串，存在一些字符只能呆在原地，无法到达其他位置
k为3时，长度为5的字符串中，第3个字符无法移动
长度为4的字符串中，$[2,3]$区间中的字符无法移动
长度为3的字符串中，$[1,3]$区间中的字符无法移动
长度为2的字符串中，$[1,2]$区间中的字符无法移动
长度为1的字符串中，$[1,1]$区间中的字符无法移动
推广：长度为n的字符串中，$[n-k+1,k]$区间中的字符无法移动，n为字符串长度
当然，具体计算出来的需要必须合法，即左端点小于等于右端点，且左端点大于等于1，右端点小于等于n

可以再进行分类，长度小于等于k的字符串中，所有字符都无法移动，长度大于k且小于等于2 * k的字符串中，在区间$[n-k+1,k]$中的字符无法移动，不在区间中的字符可以递达区间中的任意位置
无法移动的区间，采用依次比较每个字符的方式
剩下区间，采用统计每个字符出现的方式

所以对于k来说，n能分成三种情况：
$n<=k$，$k<n<2k$，$n>=2k$

#include <iostream>
#include <string>
using namespace std;

int T, n, k;
string s, t;

int main()
{
    ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
    cin >> T;
    while ( T -- )
    {
        cin >> n >> k >> s >> t;
        if (n <= k) 
        {
            if (s == t) puts("YES");
            else puts("NO");
        }
        else
        {
            int scnt[26] = {0}, tcnt[26] = {0};
            bool flag = true;
            for (int i = 0 ; i < n; ++ i ) 
            {
                scnt[s[i] - 'a'] ++ ;
                tcnt[t[i] - 'a'] ++ ;
            }
            for (int i = 0 ; i < 26; ++ i ) 
            {
                if (scnt[i] != tcnt[i])
                {
                    flag = false;
                    break;
                }
            }
            if (flag && n < 2 * k)
            {
                for (int i = n - k; i < k; ++ i )
                    if (t[i] != s[i]) 
                    {
                        flag = false;
                        break;
                    }
            }
            if (flag) puts("YES");
            else puts("NO");
        }
    }
    return 0;
};