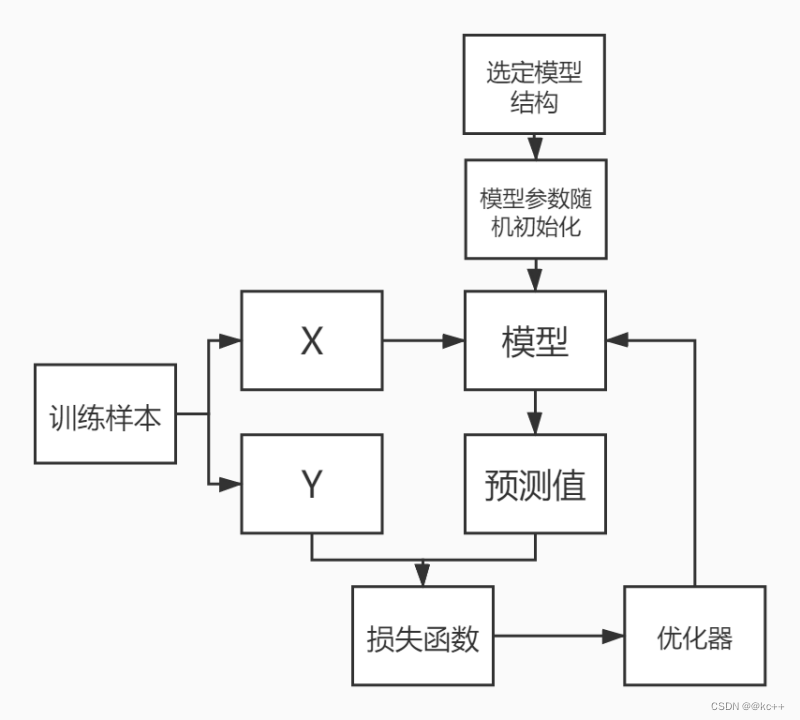
重要说明：本文从网上资料整理而来，仅记录博主学习相关知识点的过程，侵删。

一、参考资料

我所理解的卡尔曼滤波
图说卡尔曼滤波，一份通俗易懂的教程
卡尔曼滤波简单分析
How a Kalman filter works, in pictures
说说卡尔曼滤波
Extended Kalman Filter (EKF) With Python Code Example
卡尔曼滤波
卡尔曼滤波算法
SLAM 中的 Kalman Filter 推导
移动机器人技术（7.5）-- 状态估计之卡尔曼滤波与扩展卡尔曼滤波

视频资料

从放弃到精通！卡尔曼滤波从理论到实践~
【卡尔曼滤波器】_Kalman Filter_全网最详细数学推导
如何通俗并尽可能详细地解释卡尔曼滤波？

二、相关介绍

概率分布(先验，后验，似然)之Dirichlet Distribution（狄利克雷分布）

1. 概率分布

以雷达测距为例，雷达测量发现导弹有0.8的概率在7m的位置，有0.1的概率在7.2m的位置，有0.1的概率在6.9m的位置，这些数据叫做概率分布。由多个值以及这些值出现的概率组成的数据，称为概率分布。

2. 噪声误差

在使用手机上指南针软件时，明明没有动，但指南针还是会在某个范围内波动；在使用体重秤时，明明没动，但体重秤的数据不断变化。以上这些现象就是噪声误差。激光雷达、毫米波雷达、温度传感器等在使用过程中都存在噪声误差。

• 雷达在t时刻测量到导弹离目标的距离的概率分布，为$z_t=N(7,0.1^2)$，0.1就是雷达的噪声误差。
• 导弹在t-1时刻的位置的概率分布，为 $x_{t-1}=N(10,0.2^2)$ ，0.2就是上个时刻导弹位置的噪声误差。

利用卡尔曼滤波，通过融合雷达测量值和上个时刻的导弹状态数据，来减少噪声误差。主要分为两个步骤：

1. 根据上一秒导弹位置的估计值和导弹的速度（假设匀速运动），粗略估计出当前时刻导弹位置的估计值；
   $$x在t时刻的粗略估计值=x_{t-1}-v_{t-1}=N(10,0.2^2)-N(4,0.7^2)=N(6,0.2^2+0.7^2)$$

2. 根据雷达测得导弹位置的测量值和粗略估计出的导弹位置估计值，进行线性加权得到准确的导弹位置的估计值，这个值称为最优估计值。

   直接把这两个概率分布相乘，得到精确估计值的概率分布。
   $$x_t=x\text{在}t\text{时刻的粗略估计值}\times z_t=N(6,0.2^2+0.7^2)\times N(7,0.1^2)$$

   $$\begin{array}{rl}& N(6,0.2^2+0.7^2)\times N(7,0.1^2)=N(6,0.53^2)\times N(7,0.1^2)\\ & =N(\frac{6\ast 0.1^2+7\ast 0.53^2}{0.53^2+0.1^2},\frac{0.1^2\ast 0.53^2}{0.53^2+0.1^2})\end{array}$$

   $$\begin{array}{rl}& x_t=N(\frac{6\ast 0.1^2+7\ast 0.53^2}{0.53^2+0.1^2},\frac{0.1^2\ast 0.53^2}{{\left(0.53^2+0.1^2\right)}^2})=N((1-\frac{0.53^2}{0.53^2+0.1^2})\ast 6+\frac{0.53^2}{0.53^2+0.1^2}\ast 7,\\ & \frac{0.53^2+0.1^2}{{\left(0.53^2+0.1^2\right)}^2})\end{array}$$

   其中，$\frac{0.53^2}{0.53^2+0.1^2}$称为卡尔曼增益。

3. 高斯分布

高斯分布又称为正态分布，记为 $\text{N}(\mu ,{\sigma }^2)$，其中 $\mu ,\sigma$ 为正太分布的参数，分别为高斯分布的期望和方差。当这两个参数确定时，概率 $\mathbf{p}(\mathbf{x})$ 也就确定了。特别的，当 $\mu =0,{\sigma }^2=1$ 时，X 的分布为标准正态分布。高斯分布在均值位置的概率最大。

随机变量的高斯分布，其概率密度函数为：
$$\mathcal{N}(x,\mu ,\sigma )=\frac{1}{\sigma \sqrt{2\pi }}{e}^{-\frac{(x-\mu {)}^2}{2{\sigma }^2}}$$

3.1 均值与方差

在正态分布中，对于每一个随机变量X都有一个均值和方差，均值在变量的概率密度函数分布图的最中心位置，代表该数值最可能发生。方差表示变量的不确定性程度。方差作为可信度，方差越大越不可信。

均值 $\mu$ 就是数学期望 $\mu =E(X)$，方差 $D(X)={\sigma }^2=E\{[x-E(x){]}^2\}$ 是衡量随机变量离散程度的度量。方差的平方根为标准差，即为 $\sigma$。

3.2 协方差

协方差矩阵简介（Covariance Matrix）

协方差描述的是两个变量的相关程度，数学表述为：
$$\begin{array}{rl}Cov\left(X,Y\right)& =E\left[(X-E\left[X\right])\left(Y-E\left[Y\right]\right)\right]\\ & =E\left[XY\right]-2E\left[Y\right]E\left[X\right]+E\left[X\right]E\left[Y\right]\\ & =E\left[XY\right]-E\left[X\right]E\left[Y\right]\end{array}$$

3.3 高斯分布乘法公式

$$N({\mu }_1,{\sigma }_1^2)\ast N({\mu }_2,{\sigma }_2^2)=N(\frac{{\sigma }_1^2{\mu }_2+{\sigma }_2^2{\mu }_1}{{\sigma }_1^2+{\sigma }_2^2},\frac{{\sigma }_1^2{\sigma }_2^2}{{\sigma }_1^2+{\sigma }_2^2})$$

4. 贝叶斯公式

$$\text{后验概率}p(\theta |x)=\frac{\text{先验概率}p(\theta )\ast \text{似然}p(x|\theta )}{\text{全概率}P(x)}$$

其中，全概率 $P(x)$ 是与 $\theta$ 无关的常量，因此后验概率正比于先验与似然的乘积。

5. 先验概率vs后验概率

先验概率是对某一件事情发生可能性的预先客观评估，后验概率是已发生的事情由某一个原因导致的概率。

5.1 先验概率（prior）

先验概率$p(\theta )$：事件未发生，求随机变量 $\theta$ 发生的概率。

5.2 后验概率（posterior）

后验概率 $p(\theta |x)$：事件 $\mathrm{x}$ 已发生，求随机变量 $\theta$ 发生的概率。

5.3 似然概率（likelihood）

似然概率 $p(x|\theta )$：似然函数是一种参数的函数，给定特定的观测值后，描述模型参数是否合理。也就是，由“因”到导致“果”的可能性。

5.4 举例说明

有A，B，C三个随机事件，可能导致的结果是D。

• A：下雨；
• B：堵车；
• C：起晚了；
• D：迟到了。

A，B，C事件发生的概率 $P(A),P(B),P(C)$ 就是先验概率，先验概率与迟到的结果无关。

已经发生迟到事件，是由哪个事件（A，B，C）引起的概率，分别记作 $P(A|D),P(B|D),P(C|D)$，称为后验概率。

事件（A，B，C）发生时，对D迟到的描述，分别记作 $P(D|A),P(D|B),P(D|C)$，称为似然概率。迟到事件到底归咎于下雨、堵车、起晚了三个事件中的哪个比较合理？最合理的答案就是我们经常说的极大似然。

6. 观测值vs预测值

预测值，又称为估值值，是数学模型预测值(Prediction)。

观测值，又称为真实值，是传感器测量值(Measurement)，例如：激光雷达直接测量机器人离障碍物距离7m。

7. 滤波与滤波器（Filter）

filtering is weighting（滤波即加权）。滤波的作用，就是给不同的信号分量不同的权重。最简单的 loss pass filter，就是直接把低频的信号给权重1，而高频部分给权重0。对于更复杂的滤波，比如维纳滤波，则要根据信号的统计知识来设计权重。

从统计信号处理的角度，降噪可以看成滤波的一种。降噪的目的在于，突出信号本身，而抑制噪声影响。从这个角度，降噪就是给信号一个高的权重，而给噪声一个低的权重。维纳滤波就是一个典型的降噪滤波。

7.1 机器人领域的滤波算法

机器人领域的滤波算法，是指从有噪声的机器人位置数据中估计出机器人真实位置。常用的滤波算法有贝叶斯滤波、卡尔曼滤波。

根据移动模型（数学物理模型）可以得到机器人位姿和姿态的粗略估计值，然后使用滤波算法将这个粗略估计值和传感器（如GPS、陀螺仪）实际测量值融合，可以得到精确的机器人位置和姿态的估计值。

7.2 低通滤波器

低频滤波可以轻松通过的滤波器，称为低通滤波器。

8. 移动模型

给定机器人上一时刻时刻的位置信息，再给定一个控制命令，通过一系列公式计算得到执行命令后机器人预期位置。这里的一系列公式计算，就是移动模型。在实现滤波算法前，需要先对机器人进行移动模型建模，即建立机器人的移动模型。有两种常用的机器人移动模型，分别是：基于里程的运动模型，基于速度的移动模型。

基于里程的机器人移动模型

平时坐的出租车有个里程计，这个里程计可以统计轮胎转了多少距离。直观的理解，里程就是某个指标的一段变化量大小，变化量可以是距离变化也可以是角度变化。

基于里程的机器人移动模型（Odometry-based Motion Model），要解决的问题是，在已知机器人上一时刻位置和朝向角度，已知上一时刻到现在时刻这段时间内机器人预期移动距离和角度变化的情况下，求当前时刻机器人所在的位置和朝向角度。例如，已知上一时刻机器人位置坐标为（1, 0），这段时间变化量是（0.1, 0.2），移动模型会计算当前时刻机器人的位置估计：（1, 0）+ (0.1, 0.2) + (一个随机变量， 一个随机变量)。

9. 控制模型

输入控制命令和机器人的位置信息，控制模型告诉机器人执行命令后预期会走多远，身体朝向变化多少。

10. 状态估计

10.1 问题引入

以一个简单的例子，描述状态估计问题。

在一个一维空间中，沿坐标轴正向有一个坐标为 $y_0$ 的标志牌。我们原地不动，使用测距仪测出标志牌的距离为$d$。那么，我们当前的坐标 $x$ 是多少？

已知标志牌的坐标为 $y_0$，只要测量出到标志牌的距离 $d$，就可以获得我们的坐标 $x=y_0-d$。

但是，我们的测量仪存在误差，计算的结果并不准确，那我们可以这样考虑：既然我们没有移动，那我们可以测量多次，取平均值。到此，我们完整的构建了一个状态估计问题：

• 在一个一维空间里，估算自己的坐标 $x$；
• 给出一个解决方案：由于告知了标志牌的坐标 $y_0$，可以以其作为参考；
• 使用测量仪测量自身到标志牌的距离 $d$，以此反算出自己的坐标 $x$。

我们姑且称之为“估计”，因为我们不可能有无限的时间来进行无限次的测量，从而获得坐标 $x$ 的真实值。而是在测量次数足够多时，便认为结果已经足够准确，即通过一些手段去逼近真实值。

10.2 状态估计相关概念

以上的例子，可以解释什么是离散时间的、线性、时不变、高斯系统的状态估计。具体来说，可以解释为：

• 离散时间(discrete-time)：描述了我们的测量手段并不是时间连续的；

• 线性(linear)：描述了传感器（测距仪）数学模型的类型。由于是与对参照物进行观测有关的方程，我们也称之为：观测方程/观测模型(observation model)。通过参考物 $y$ 以及测距结果 $d$，推算出自身坐标 $x$，即 $x=f(y,d)=y-d$，该模型为线性函数；

• 时不变(time-invariant)：传感器数学模型中的映射关系，不随时间变化。时不变并不是指待估计状态 $x$ 不随时间变化，它指与状态的映射关系 $f:x,y\to d$ 不随时间变化。简单来说，这里指观测方程不随时间变化。例如：观测方程 $f(x,y)=y-x$ 不会变为 $f(x,y)=y-2x$ 等其他映射关系；

• 高斯分布(gaussian distribution)：描述测量噪声的类型。测量噪声 $n$ 服从高斯分布。

  考虑到测距仪存在误差，即存在测量噪声，而测量值 $d$ 实际是真实值与测量噪声结合后的结果。因此，需要完善测量方程，在理论结果的基础上增加一个测量噪声 $n$。公式如下所示：
  $$d=\underset{\text{theoretical result}=d_{true}}{\underbrace{f(x,y)}}+n$$
  一种比较理想的情况是，这个测量噪声 n 是高斯分布的。

10.3 基于大数定律的测量值

服从高斯分布的测量噪声是一个随机变量，在重复测量时，所得到的结果不尽相同，在真实值附近波动。但在测量次数 $K$ 足够大时，此种噪声项的累加将趋于均值。如果噪声的均值为0，那么可以近似地得到准确结果：
$$\begin{array}{rl}{d}_{mean}& =\frac{1}{K}\sum d_k\\ & =d_{true}+\underset{\approx 0}{\underbrace{\frac{1}{K}\sum _{\approx 0}{n}_k}}\\ & \approx d_{true}\end{array}$$

三、卡尔曼滤波宏观理解

卡尔曼滤波系列1——卡尔曼滤波

卡尔曼滤波算法，是一种递推预测滤波算法，算法中涉及到滤波，也涉及到对下一时刻数据的预测。

1. 卡尔曼滤波引入

下面举一个生活中的小例子来引入卡尔曼滤波：现有一枚硬币、一把尺子，目的是尽可能准确的得出硬币的尺寸，共测量k次，每次的测量结果记为 $Z_1,Z_2,\dots Z_k$。我们如何估计硬币的尺寸呢？很自然的一个想法是取平均值，计算过程如下图：

简单理解就是，估计某次测量的结果是和估计上次的结果有关系的，这体现了卡尔曼滤波的递归思想。用公式表示为：

当前估计值 = 上一次的估计值 + 系数*(当前测量值 - 上一次的估计值)

$${\hat{\mathrm{X}}}_k={\hat{\mathrm{X}}}_{k-1}+\frac{1}{k}(Z_k-{\hat{\mathrm{X}}}_{k-1})$$

参数解释

• ${\hat{\mathrm{X}}}_k$ 表示第k次的估计值
• $Z_k$表示第k次的测量值；
• ${\hat{\mathrm{X}}}_{k-1}$ 表示第k-1次的估计值；

由上式可知，第k次估计值 = 第k-1次估计值 + $\frac{1}{k}$ （第k次测量值 - 第k-1次估计值）。若随着测量的次数k增大， $\frac{1}{k}$ 将趋于0，上式将变为：${\hat{\mathrm{X}}}_k={\hat{\mathrm{X}}}_{k-1}$ ，即随着k的增大，第k次的估计值只和第（k-1）次的估计值有关，而与第k次的测量值无关，也即随着k增大，测量结果不在重要。其实这也非常好理解，当我们测量了很多次，前面的估计值其实已经非常接近真实值了，所以再多测一次的意义就变得不大了；相反的，若k非常小，即k=1（k表示测量次数，k=0无意义）时，上式将为：${\hat{\mathrm{X}}}_k=Z_k$，即此时的估计值完全由测量值决定。

2. 卡尔曼系数

将上式中的 $\frac{1}{k}$ 替换为 ${\text{K}}_k$ 表示，${\text{K}}_k$ 就是卡尔曼系数。

${\text{K}}_k$ 的计算公式，如下图所示：

宏观理解该公式：

• 当 $e_{EST}\gg e_{MEA}$ 时，即估计误差远大于测量误差时，${\text{K}}_k$ 趋于1，${\hat{\mathrm{X}}}_k$ 趋向于 $Z_k$ ，表示相信测量值。
• 当 $e_{EST}\ll e_{MEA}$ 时，即估计误差远小于测量误差时，${\text{K}}_k$ 趋于0，${\hat{\mathrm{X}}}_k$ 趋向于 ${\hat{\mathrm{X}}}_{k-1}$ ，表示相信估计值。

3. 卡尔曼滤波数据融合

本章通过一个简单的例子，体现卡尔曼滤波数据融合的作用。

现有一个电子秤和一个普通秤，同时测一个物体，电子秤测得的重量结果为Z1=30，标准差为 ${\sigma }_1=2$；普通秤测得的重量结果为Z2=32，标准差为 ${\sigma }_1=4$。

假设它们是满足正态分布，可以画出两种秤测得物体重量的分布图，如下：

上图Z1表示电子秤测量结果分布情况，Z2表示普通秤测量结果分布情况。在没进行计算之前，我觉得我们可以先猜一下真实值。由上可知，电子秤的标准差只有2，而普通秤的标准差为4，这表示电子秤测量结果更加稳定，这样测量结果可能更加准确，最终我们融合的结果可能就更加偏向于电子秤测得的结果，即更接近于30。当然这些仅是我的猜测结果，现我们通过计算看看最优的估计值是否和我们的猜测一致。

将第一次测量结果Z1作为估计值，第二次测量结果Z2作为测量值，这样我们就可以得到估计值 $\hat{\mathrm{Z}}$ 的表达式，如下：
$$\hat{Z}=Z_1+k\left(Z_2-Z_1\right)$$
为了使得 $\hat{\mathrm{Z}}$ 最优，需要使 $\hat{\mathrm{Z}}$ 的标准差 ${\sigma }_{\hat{Z}}$ 最小，也即方差 $\mathrm{v}\mathrm{ar}\left(\hat{Z}\right)$ 最小，推导公式如下：

上图得到公式：${{\sigma }_{\hat{Z}}}^2={\left(1-\mathrm{k}\right)}^2{{\sigma }_1}^2+k^2{{\sigma }_2}^2$，为了使 ${{\sigma }_{\hat{Z}}}^2$ 最小，需要求得k。令上式对k求导等于0，找到极值点即可，求导如下图所示：

至此我们得到了最终的估计值和标准差，可以看到这个结果和我们之前猜测的一样更加的接近30，而且可以发现这个结果的标准差比之前的两次测量的标准差都要小。画出三次结果的分布图，如下图所示：

after_merge表示融合后的结果，从上图可以看出，融合后的结果分布更高更瘦，其效果更好。

4. 通俗理解卡尔曼滤波

如何通俗并尽可能详细地解释卡尔曼滤波？

假设养了一头猪：

一周前，这只猪的体重是46±0.5kg。注意，在这里我用了±0.5，表示其实我对这只猪一周前的体重并不是那么确定的，也就是说，46kg这个体重有0.5kg的误差。

现在，我又养了一个星期。那么我想要知道它一个星期之后多重，又大概有多少的误差？

为了得到一周后的体重，我有两种方法：一是根据我多年的养猪经验得到的猪体重公式推求出一个大概的值，另一个就是直接去称它的体重。当然，两种方法都有一定的误差。假设经验公式得到的体重是48kg，误差2kg；直接称体重得到的是49kg，误差1kg。

可是，我是一个处女座的人，不管是经验公式得到的值，还是直接称量得到的值，我都觉得不够准。我希望有一种方法，可以同时结合这只猪一周前的体重、用经验公式估计的值以及直接称量得到的值，综合考虑，得出一个最接近猪真实体重的，误差最小的值。这就是卡尔曼滤波要完成的任务。

现在我们来把养猪的模型抽象成数学公式：

上图的左边，上一周的猪的体重，可以抽象为也k-1时刻的状态值，用k-1时刻的最优估计值加上一个误差项来表示，右边同理。其中，
$${\mathcal{P}}_{\mathrm{k}}=\mathbb{E}\left[{\mathbf{e}}_{\mathrm{k}}{\mathbf{e}}_{\mathrm{k}}^{\mathrm{T}}\right]$$
这一项表示的是估计值的协方差。这里要说明两点：

1. 上图中所有的变量都是用粗体，表示这是一个向量或者一个矩阵；
2. 之所以用（列）向量而非一个数来表示状态值，是因为，虽然一只猪的体重可以用一个值来表示，但是在实际的应用中很多状态并不是一个数就能表示的（比如导弹在空间中的位置，同时有x、y、z三个坐标）。

上图中右边表示k时刻的状态值，这个值可以通过预测模块（也就是根据经验公式估计猪的体重）和纠错模块（也就是直接去称量猪的体重值）来估计。同样，预测模块和纠错模块都有着对应的误差和误差协方差矩阵。卡尔曼滤波要做的，就是根据贝叶斯估计的相关理论，同时考虑预测模块和纠错模块的协方差，对误差小的项赋予较大的权重，对误差大的项赋予较小的权重，并使预测的误差最小。

具体的实现过程如下：

四、卡尔曼滤波相关介绍

1. 引言

卡尔曼滤波由一系列递归数学公式描述，它提供了一种高效可计算的方法来估计过程的状态，并使估计均方差误差最小。卡尔曼滤波器应用广泛且功能强大，可以估计信号的过去状态、当前状态、未来状态。

卡尔曼滤波(Kalman Filter, KF)是一种优化估算算法(Optimal Estimation Algorithm)，常用于无人机、自动驾驶、卫星导航、计算机视觉、信号处理等领域，包括机器人导航控制系统、制导系统、传感器数据融合系统，以及军事方面的雷达系统、导弹追踪系统等。实际作用主要是：基于传感器测量值来更新预测值，以达到更精确的估计。

2. 适用场景

卡尔曼滤波适用于估计一个由随机变量组成的动态系统的最优状态。即便是观测到的系统状态参数含有噪声，观测值不准确，卡尔曼滤波也能够完成对状态真实值的最优估计。

卡尔曼滤波算法的本质是，利用两个正态分布的融合仍是正态分布这一特性进行迭代。

3. 状态观察器

状态观察器(State Observers)：用于优化估算一些无法直接测量但可以间接测量的状态。

场景: 观察火箭喷射器的内部温度

现在有一只火箭要从地球飞往火星，火箭使用液态氢作为燃料，但过高温度会导致火箭喷射器的机械部件损坏，因此监控喷射器内部温度就十分重要，可传感器不支持放置在喷射器内部，否则会被融化掉。但我们可以在喷射器外部的放置温度传感器，间接测量内部温度。但间接测量值和真实值存在误差，为此，我们可以使用状态观察器去基于间接测量值估算出真实值。

4. 最佳状态估计器

最佳状态估计器(Optimal State Estimator): 从受误差影响的传感器测量中估算出最佳的系统状态。

卡尔曼滤波本身便是一个最佳状态估计器，它跟前面讲的状态观察器差不多，不同的是KF是为随机系统设计的。状态观测器和最佳状态估计器(KF)的预测值公式如下：
$$\text{State observer}{\hat{x}}_{k+1}=A{\hat{x}}_k+B{u}_k+K(y_k-C{\hat{x}}_k)\text{Deterministic system}$$

$$\text{Kalman filter}{\hat{x}}_k=A{\hat{x}}_{k-1}+B{u}_k+K_k(y_k-C(A{\hat{x}}_{k-1}+B{u}_k))\text{Stochastic system}$$

场景: 估算隧道内汽车的位置

如果汽车进入隧道，汽车上的GPS接收器很难接收到卫星信号。如果在周围有高建筑物遮挡的街道上行驶，因为多路径效应(Multipath Effect，即信号失真)，导致定位噪声很大。我们可以简单看作这是一个传感器测量受误差影响的案例，如果我们想估算出汽车真实的位置状态，建议使用卡尔曼滤波。

KF的目标是将GPS测量值(Measurement)和数学模型预测值(Prediction)相结合取找到汽车位置的最优估计状态(即汽车位置)。

5. 卡尔曼增益

例如，激光雷达测量机器人离障碍物的举例为7m，准确度为90%，根据速度估计机器人离障碍物的距离为6m，准确度为80%，最终的距离估计结果为：
$$result=(1-\frac{0.9}{0.8+0.9})\ast 6+\frac{0.9}{0.8+0.9}\ast 7=6.52\text{ 米}.$$
其中，$\frac{0.9}{0.8+0.9}$ 称为卡尔曼增益，表示这个传感器数据相对于根据速度计算出的估计值的靠谱程度。

6. 其他卡尔曼滤波

卡尔曼滤波是线性的，而实际中，很多数据模型是非线性的，此时可以考虑扩展卡尔曼滤波，另外，有兴趣的朋友也可以去了解无迹卡尔曼滤波和粒子滤波，如图12所示。

五、卡尔曼滤波库

simdkalman

simdkalman

Python实现卡尔曼滤波

[易懂]如何理解那个把嫦娥送上天的卡尔曼滤波算法Kalman filter?

假设导弹做水平运动，导弹每个时刻的速度为dv，速度测量仪的标准差是v_std，每个时刻用GPS传感器测量出导弹位置position_noise以及GPS的方差是predict_var。

# -*- coding: utf-8 -*-

import numpy as np


t = np.linspace(1,100,100) # 在1~100s内采样100次
a = 0.5 # 加速度值
position = (a * t**2)/2

position_noise = position+np.random.normal(0,120,size=(t.shape[0])) # 模拟生成GPS位置测量数据（带噪声）
import matplotlib.pyplot as plt
plt.plot(t,position,label='truth position')
plt.plot(t,position_noise,label='only use measured position')


#---------------卡尔曼滤波----------------
# 初始的估计导弹的位置就直接用GPS测量的位置
predicts = [position_noise[0]]
position_predict = predicts[0]

predict_var = 0
odo_var = 120**2 #这是我们自己设定的位置测量仪器的方差，越大则测量值占比越低
v_std = 50 # 测量仪器的方差（这个方差在现实生活中是需要我们进行传感器标定才能算出来的，可搜Allan方差标定）
for i in range(1,t.shape[0]):
  
    dv =  (position[i]-position[i-1]) + np.random.normal(0,50) # 模拟从IMU读取出的速度
    position_predict = position_predict + dv # 利用上个时刻的位置和速度预测当前位置
    predict_var += v_std**2 # 更新预测数据的方差
    # 下面是Kalman滤波
    position_predict = position_predict*odo_var/(predict_var + odo_var)+position_noise[i]*predict_var/(predict_var + odo_var)
    # 高斯分布乘法公式
    predict_var = (predict_var * odo_var)/(predict_var + odo_var)
    predicts.append(position_predict)

    
plt.plot(t,predicts,label='kalman filtered position')

plt.legend()
plt.show()