为什么需要激活函数?激活函数的作用?
- 激活函数可以引入非线性因素,可以学习到复杂的任务或函数。如果不使用激活函数,则输出信号仅是一个简单的线性函数。线性函数一个一级多项式,线性方程的复杂度有限,从数据中学习复杂函数映射的能力很小。
- 激活函数可以把当前特征空间通过一定的线性映射转换到另一个空间,让数据能够更
好的被分类;
为什么激活函数需要非线性函数?
- 假若网络中全部是线性部件,那么线性的组合还是线性,与单独一个线性分类器无异。这样就做不到用非线性来逼近任意函数;
- 使用非线性激活函数
f
(
x
)
f(x)
f(x),以便使网络更加强大,增加它的能力,使它可以学习复杂
的事物,复杂的表单数据,以及表示输入输出之间非线性的复杂的任意函数映射。使用非线性
激活函数,能够从输入输出之间生成非线性映射;
激活函数的选择
- 如果输出是0、1 值(二分类问题),则输出层选择sigmoid 函数,然后其它的所有单元都选择Relu 函数。
- 如果在隐藏层上不确定使用哪个激活函数,那么通常会使用Relu 激活函数。有时,也会使用tanh 激活函数,但Relu 的一个优点是:当是负值的时候,导数等于0。
- sigmoid 激活函数:除了输出层是一个二分类问题基本不会用它。
- tanh 激活函数:tanh 是非常优秀的,几乎适合所有场合。
- ReLu 激活函数:最常用的默认函数,如果不确定用哪个激活函数,就使用ReLu 或者Leaky ReLu,再去尝试其他的激活函数。
ReLu 激活函数的优点
- 计算更快&学习更快: ReLu 激活函数的导数都会远大于0,在程序实现就是一个if-else 语句,而sigmoid 函数需要进行浮点四则运算,在实践中,使用ReLu 激活函数神经网络通常会比使用sigmoid 或者tanh 激活函数学习的更快。
- 防止梯度弥散: sigmoid 和tanh 函数的导数在正负饱和区的梯度都会接近于0,这会造成梯度弥散,而Relu 和Leaky ReLu 函数大于0 部分都为常数,不会产生梯度弥散现象。
- 稀疏激活性: 从信号方面来看,即神经元同时只对输入信号的少部分选择性响应,大量信号被刻意的屏蔽了,这样可以提高学习的精度,更好更快地提取稀疏特征。当 x < 0 x<0 x<0 时,梯度为0,ReLU硬饱和,而当 x > 0 x>0 x>0 时,则不存在饱和问题。ReLU 能够在 x > 0 x>0 x>0 时保持梯度不衰减,从而缓解梯度消失问题。
常见的激活函数
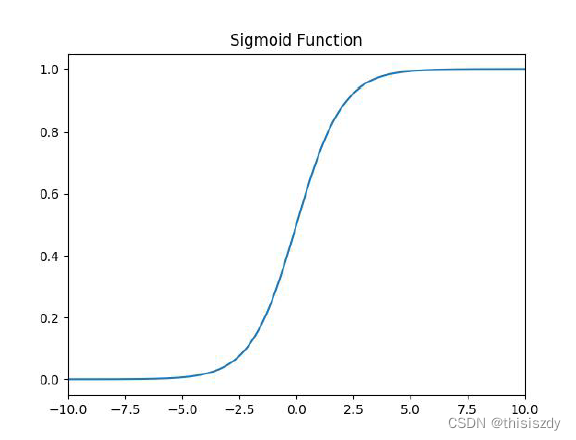
1、Sigmod函数
f
(
x
)
=
1
1
+
e
−
x
f(x)= \frac {1}{1+e^{-x}}
f(x)=1+e−x1
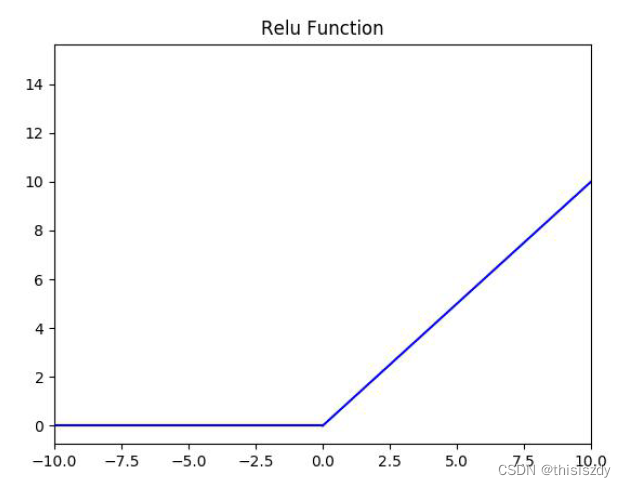
2、Relu函数
f
(
x
)
=
m
a
x
(
0
,
x
)
f(x)=max(0,x)
f(x)=max(0,x)
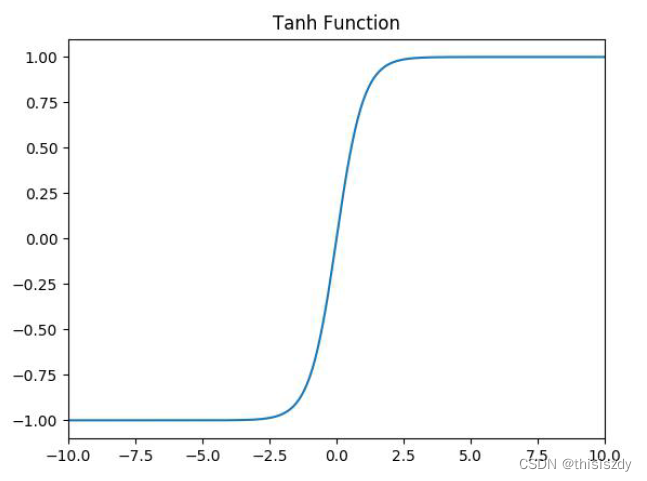
3、tanh函数
f
(
x
)
=
e
x
−
e
−
x
e
x
+
e
−
x
f(x)=\frac {e^{x}-e^{-x}}{e^{x}+e^{-x}}
f(x)=ex+e−xex−e−x
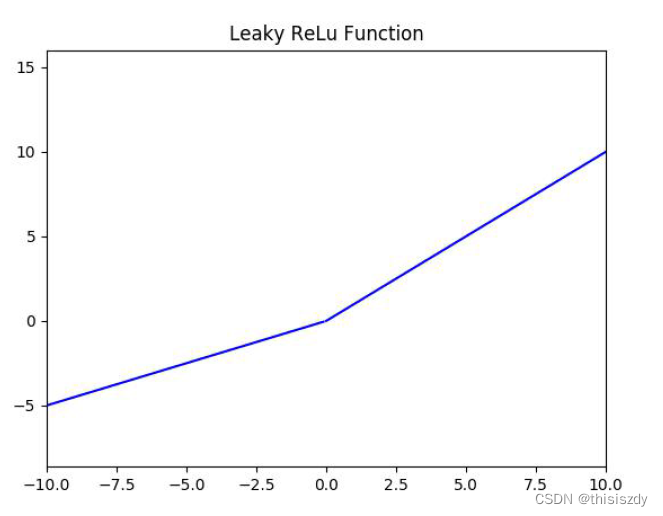
4、Leak Relu函数
f
(
x
)
=
{
α
x
,
x
<
0
x
,
x
>
0
f(x)=\left\{ \begin{aligned} \alpha x, x<0\\ x,x>0 \\ \end{aligned} \right.
f(x)={αx,x<0x,x>0
图为
α
=
0.5
\alpha=0.5
α=0.5
5、softmax函数
softmax多用于多分类神经网络的输出
σ
(
z
)
j
=
e
z
j
∑
k
=
1
K
e
z
k
\sigma(z)_{j}=\frac {e^{z_{j}}}{\sum _{k=1}^{K} e^{z_{k}}}
σ(z)j=∑k=1Kezkezj