超参数的选择-手工搜索、网格搜索、随机搜索、贝叶斯搜索

news2024/11/23 19:24:24

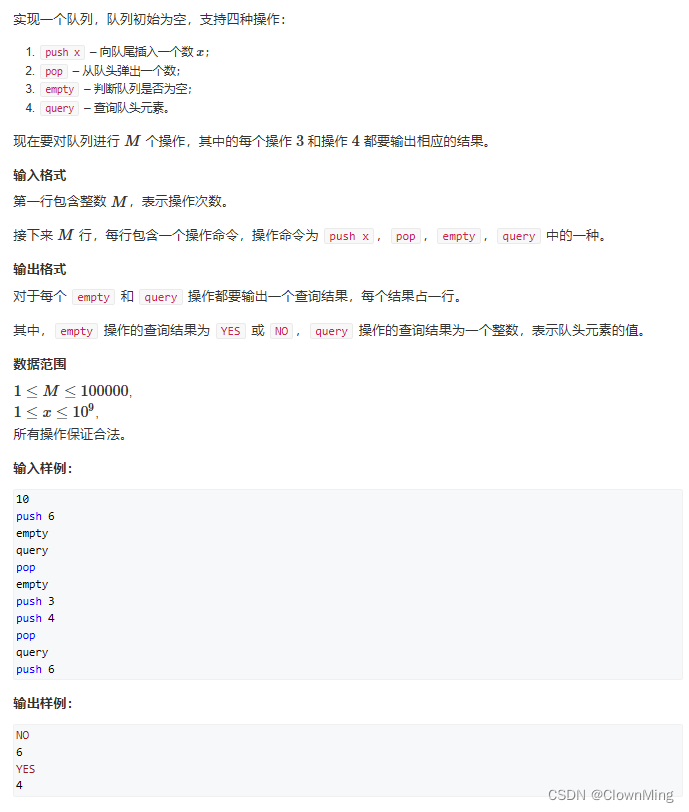
超参数：超参数是在建立模型时用于控制算法行为的参数。这些参数不能从常规训练过程中获得。在对模型进行训练之前，需要对它们进行赋值。

  • 超参数与模型的参数不同。模型参数(如神经网络的权重)是在训练过程中学习得到的,而超参数(如学习率、隐藏层数量)需要在训练前指定。

  • 超参数直接影响模型的表现能力和复杂度。学习率过高易导致收敛失败,学习率过低训练时间长;网络结构过大易过拟合,过小预测能力差，网络结构过大的话模型结构复杂容易过拟合，网络结构比较小的话模型结构简单可能不能完全拟合数据，预测能力较差。

  • 找到最优超参数需要通过网格/随机搜索等方法,根据验证集效果来选择，根据不一样的数据选择不同的搜索方法，这是模型优化的重要一步。

  • 随着模型结构和规模不断增大,自动机器学习正试图构建更智能高效的超参数搜索策略。

  • 不同数据集上同一组超参数效果可能不同，需要根据数据特征重新确定超参数范围与最优值，不一样的数据集的需要选择的超参数的范围不同。

ML工作流中最困难的部分之一是为模型找到最好的超参数，ML模型的性能与超参数直接相关，

  1. 不同模型的超参数种类和范围都不相同。例如神经网络中的学习率、层数、隐藏单元数等,决策树中的最大深度、最小样本数等。

  2. 最佳超参数取决于数据集的特点和模型的类型。同一组超参数在不同数据集上效果可能很不同。

  3. 通常采用网格搜索、随机搜索等方法来遍历超参数空间,选择验证集效果最好的一组作为最佳超参数。

  4. 随着数据集和计算资源的增加,超参数优化变得更加关键。一些自动机器学习技术正尝试开发更智能的超参数搜索策略。

  5. 一个合理的流程是:先使用网格/随机搜索粗略找到较好区域,然后使用贝叶斯优化等精细优化技术逼近最优解。

  6. 过拟合也需要通过方法如正则化来控制,最佳超参数不一定意味着在测试集上的性能最好。

总之,找到模型的最佳超参数是一个系统工程问题,需要理解数据特征,灵活使用不同搜索方法,注意过拟合问题。这也是ML领域仍在持续研究和改进的一个重要方向。

1.传统手工搜索

在传统的调参过程中，我们通过训练算法手动检查随机超参数集，并选择符合我们目标的最佳参数集。

#importing required libraries
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import train_test_split
from sklearn.model_selection import KFold , cross_val_score
from sklearn.datasets import load_wine

wine = load_wine()
X = wine.data
y = wine.target
#splitting the data into train and test set
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size = 0.3,random_state = 14)
#declaring parameters grid
k_value = list(range(2,11))
algorithm = ['auto','ball_tree','kd_tree','brute']
scores = []
best_comb = []
kfold = KFold(n_splits=5)

#hyperparameter tunning
for algo in algorithm:
  for k in k_value:
    knn = KNeighborsClassifier(n_neighbors=k,algorithm=algo)
    results = cross_val_score(knn,X_train,y_train,cv = kfold)

    print(f'Score:{round(results.mean(),4)} with algo = {algo} , K = {k}')
    scores.append(results.mean())
    best_comb.append((k,algo))

best_param = best_comb[scores.index(max(scores))]
print(f'\nThe Best Score : {max(scores)}')
print(f"['algorithm': {best_param[1]} ,'n_neighbors': {best_param[0]}]")

我们可以看到这里是选择了knn模型的得分来找出最优参数，通过判断各项组合的得分哪个更高，这里K值是选取的2-10共9个数，算法是选取了四种算法，同时此时是进行了五折交叉验证，用于对数据进行K折分割，将数据分成五个相等的折，用其中的4个数据进行训练1个数据进行测试，一共进行5次训练测试，相比简单的训练测试，这种交叉验证方法可以减少模型评估的差异性。K=5是一个平衡了偏差和计算成本的常见选择，K值越大，偏差越小，但是大的K值带来的就是计算成本的增加，所以K=5此时是一个折中的最优选择。

首先遍历所有的算法，其次遍历所有的可选择的K值，选取KNN算法进行比较，进行五折交叉验证。此时打印结果，将交叉验证的五次结果取平均之后保留四位小数，同时使用的是什么算法还有此时的K值选取的是什么。

print(f'Score:{round(results.mean(),4)} with algo = {algo} , K = {k}')

 

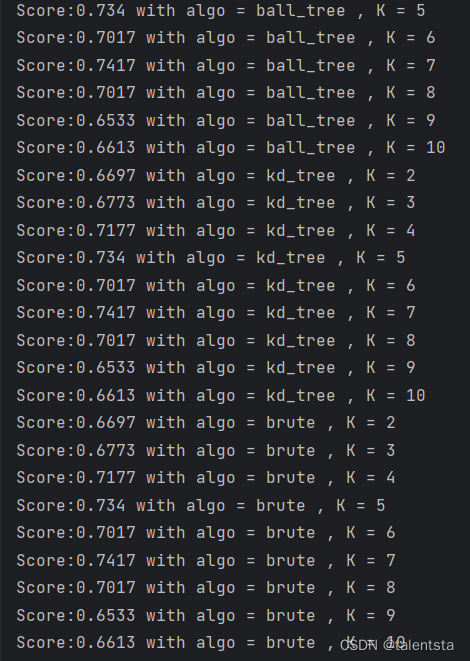
将每一次交叉验证结果的平均值都放入 scores 列表中，同时将每一次选取的K值和使用的算法都放入 best_comb 列表中。

要找出最好的参数此时是找出此时得分最高的对应的分数中的索引，再从 best_comb 中找出相对应位置的索引参数。

best_param = best_comb[scores.index(max(scores))]

这行代码是为了获取交叉验证得分最高的参数组合。

具体来说:

  • best_comb是一个参数组合列表,包含了交叉验证时试验过的所有参数组合。

  • scores是一个对应每个参数组合的交叉验证得分列表。

  • max(scores)获取了得分列表中的最大值,也就是最优得分。

  • scores.index(max(scores)) 获取该最大得分对应在scores列表中的索引。

  • 将这个索引用来从best_comb列表中获取对应参数组合。

所以通过这行代码,我们最终获得了交叉验证得分最大,也就是性能最优的参数组合best_param。

print(best_comb)

 

[(2, 'auto'), (3, 'auto'), (4, 'auto'), (5, 'auto'), (6, 'auto'),
 (7, 'auto'), (8, 'auto'), (9, 'auto'), (10, 'auto'), (2, 'ball_tree'),
 (3, 'ball_tree'), (4, 'ball_tree'), (5, 'ball_tree'), (6, 'ball_tree'), 
(7, 'ball_tree'), (8, 'ball_tree'), (9, 'ball_tree'), (10, 'ball_tree'), 
(2, 'kd_tree'), (3, 'kd_tree'), (4, 'kd_tree'), (5, 'kd_tree'), (6, 'kd_tree'),
 (7, 'kd_tree'), (8, 'kd_tree'), (9, 'kd_tree'), (10, 'kd_tree'), (2, 'brute'),
 (3, 'brute'), (4, 'brute'), (5, 'brute'), (6, 'brute'), (7, 'brute'), 
(8, 'brute'), (9, 'brute'), (10, 'brute')]

best_comb 打印出的结果是这样的，所以可根据索引找出最佳参数。

print(f'\nThe Best Score : {max(scores)}')
print(f"['algorithm': {best_param[1]} ,'n_neighbors': {best_param[0]}]")
The Best Score : 0.7416666666666667
['algorithm': auto ,'n_neighbors': 7]

根据如上图所示的打印结果，我们可看到最高得分结果同时最高得分对应的索引 best_comb,再分别找出其算法和对应的选取的近邻个数。

二、网格搜索

网格搜索是一种基本的超参数调优技术。它类似于手动调优，为网格中指定的所有给定超参数值的每个排列构建模型，评估并选择最佳模型。考虑上面的例子，其中两个超参数k_value =[2,3,4,5,6,7,8,9,10] & algorithm =['auto','ball_tree','kd_tree','brute']，在这个例子中，它总共构建了9*4 = 36不同的模型。

from sklearn.model_selection import GridSearchCV

knn = KNeighborsClassifier()
grid_param = { 'n_neighbors' : list(range(2,11)) , 
              'algorithm' : ['auto','ball_tree','kd_tree','brute'] }
              
grid = GridSearchCV(knn,grid_param,cv = 5)
grid.fit(X_train,y_train)
#best parameter combination
grid.best_params_
#Score achieved with best parameter combination
grid.best_score_
#all combinations of hyperparameters
grid.cv_results_['params']
#average scores of cross-validation
grid.cv_results_['mean_test_score']

此时我们看到网格搜索此时可以直接调用出来，此时选用的模型也是 K 近邻分类器，此时我们可以事先放置好需要进行网格搜索的参数，包括 n_neighbors 和 algorithm,此时再进行网格搜索便可直接进行参数放置和训练，相比传统手工搜索使用起来更加方便一些，不用使用 for 函数再进行遍历。

grid = GridSearchCV(knn,grid_param,cv = 5)
grid.fit(X_train,y_train)

  • grid.best_params_: 获取的是交叉验证后性能最优的那组超参数设置

  • grid.best_score_: 获取交叉验证时用最优参数集得分

  • grid.cv_results_['params']: 获取超参数所有试验组合

  • grid.cv_results_['mean_test_score']: 获取每个超参数组合的交叉验证平均分数

GridSearchCV会尝试所有指定的超参数组合,通过交叉验证获取每个组合的性能,从中选择得分最高的作为最优参数。

这几个属性可以直接获取GridSearchCV的主要结果:

  • best_params_获取最优参数
  • best_score_获取最优得分
  • cv_results_['params']查看所有试验过的组合
  • cv_results_['mean_test_score']查看每个组合的交叉验证得分

它们对于分析和tracked GridSearchCV过程很重要,可以直接得到搜索结果而无需进一步计算。常用于报告和评估参数调优结果。

所以这些代码通过访问GridSearchCV对象的内置属性,方便高效地获取其网格搜索交叉验证的各项结果。

{'algorithm': 'auto', 'n_neighbors': 5}
0.774
[{'algorithm': 'auto', 'n_neighbors': 2}, {'algorithm': 'auto', 'n_neighbors': 3}, {'algorithm': 'auto', 'n_neighbors': 4}, {'algorithm': 'auto', 'n_neighbors': 5}, {'algorithm': 'auto', 'n_neighbors': 6}, {'algorithm': 'auto', 'n_neighbors': 7}, {'algorithm': 'auto', 'n_neighbors': 8}, {'algorithm': 'auto', 'n_neighbors': 9}, {'algorithm': 'auto', 'n_neighbors': 10}, {'algorithm': 'ball_tree', 'n_neighbors': 2}, {'algorithm': 'ball_tree', 'n_neighbors': 3}, {'algorithm': 'ball_tree', 'n_neighbors': 4}, {'algorithm': 'ball_tree', 'n_neighbors': 5}, {'algorithm': 'ball_tree', 'n_neighbors': 6}, {'algorithm': 'ball_tree', 'n_neighbors': 7}, {'algorithm': 'ball_tree', 'n_neighbors': 8}, {'algorithm': 'ball_tree', 'n_neighbors': 9}, {'algorithm': 'ball_tree', 'n_neighbors': 10}, {'algorithm': 'kd_tree', 'n_neighbors': 2}, {'algorithm': 'kd_tree', 'n_neighbors': 3}, {'algorithm': 'kd_tree', 'n_neighbors': 4}, {'algorithm': 'kd_tree', 'n_neighbors': 5}, {'algorithm': 'kd_tree', 'n_neighbors': 6}, {'algorithm': 'kd_tree', 'n_neighbors': 7}, {'algorithm': 'kd_tree', 'n_neighbors': 8}, {'algorithm': 'kd_tree', 'n_neighbors': 9}, {'algorithm': 'kd_tree', 'n_neighbors': 10}, {'algorithm': 'brute', 'n_neighbors': 2}, {'algorithm': 'brute', 'n_neighbors': 3}, {'algorithm': 'brute', 'n_neighbors': 4}, {'algorithm': 'brute', 'n_neighbors': 5}, {'algorithm': 'brute', 'n_neighbors': 6}, {'algorithm': 'brute', 'n_neighbors': 7}, {'algorithm': 'brute', 'n_neighbors': 8}, {'algorithm': 'brute', 'n_neighbors': 9}, {'algorithm': 'brute', 'n_neighbors': 10}]
[0.66966667 0.66933333 0.70966667 0.774      0.70966667 0.72566667
 0.71766667 0.66933333 0.66133333 0.66966667 0.66933333 0.70966667
 0.774      0.70966667 0.72566667 0.71766667 0.66933333 0.66133333
 0.66966667 0.66933333 0.70966667 0.774      0.70966667 0.72566667
 0.71766667 0.66933333 0.66133333 0.66966667 0.66933333 0.70966667
 0.774      0.70966667 0.72566667 0.71766667 0.66933333 0.66133333]

GridSearchCV因为需要试遍所有的超参数组合,计算量很大,导致它的计算速度非常慢。

这里有几点原因导致GridSearchCV计算速度慢:

  • 每个超参数组合都需要训练一个模型并进行交叉验证,这是必须重复执行的计算步骤。

  • 随着超参数组合数量的增加,计算量呈指数级增长。即使只增加一个新的超参数值,都会显著增加计算量。

  • 交叉验证本身也需要重复训练/测试过程,加重了计算负担。

  • 对于大规模数据集或复杂的模型(深度学习等),单个训练过程的时间长,搜索过程更慢。

解决这一问题,有以下几种方法可以减轻计算负担:

  • 减少超参数组合数量,只选择关键参数或有限值范围
  • 使用并行计算利用多核CPU/GPU加速
  • 使用随机搜索而非穷尽搜索,降低每个组合的重复计算
  • 根据初步结果进行早停,跳过非优参数组合
  • 使用Gradient Boosted Trees或Bayesian优化进行更智能搜索

GridSearchCV的“点遍尝试”策略导致计算量巨大,在实际应用中速度通常是首要问题需要考虑优化，这提供了其他超参数优化技术的发挥空间

 

三、随机搜索

使用随机搜索代替网格搜索的动机是，在许多情况下，所有的超参数可能不是同等重要的。随机搜索从超参数空间中随机选择参数组合，参数由n_iter给定的固定迭代次数的情况下选择。实验证明，随机搜索的结果优于网格搜索。

from sklearn.model_selection import RandomizedSearchCV

knn = KNeighborsClassifier()

grid_param = { 'n_neighbors' : list(range(2,11)) , 
              'algorithm' : ['auto','ball_tree','kd_tree','brute'] }

rand_ser = RandomizedSearchCV(knn,grid_param,n_iter=10)
rand_ser.fit(X_train,y_train)
#best parameter combination
rand_ser.best_params_
#score achieved with best parameter combination
rand_ser.best_score_
#all combinations of hyperparameters
rand_ser.cv_results_['params']
#average scores of cross-validation
rand_ser.cv_results_['mean_test_score']

这里我们可以看到随机搜索与网格搜索在程序上的区别只是换了一个调用的算法，由之前的网格搜索换成了随机搜索。

搜索次数n_iter=10这个细节需要解释一下:

因此,随机搜索更适用于:

而对于关键任务,如生产模型,还是推荐使用全面搜索GridSearchCV,获得全局最优参数作为进一步研究的依据。

  • n_iter参数指定RandomizedSearchCV进行随机搜索的次数。

  • 每一次搜索,它会随机选择一个超参数组合进行模型训练和验证。

  • 设定n_iter=10意味着RandomizedSearchCV将会随机选择10个不同的超参数组合进行验证。

  • 与全面搜索 GridSearchCV相比,n_iter=10的搜索次数较低,所以计算速度更快。

  • 但是搜索次数太低,可能无法找到真正的最优超参数,搜索效果不如 GridSearchCV。

  • 一般来说,n_iter的数量需要根据问题的复杂度进行适当增大,以平衡速度和效果:

    • 对于简单模型和数据,n_iter=10-30可能足够

    • 对于复杂模型或大数据,可以设定n_iter=50-100

  • 如果计算资源限制较大,也可以采用更低n_iter进行初步搜索,找到优良区域再用高n_iter精细搜索。

  • {'n_neighbors': 5, 'algorithm': 'ball_tree'}
0.774
[{'n_neighbors': 7, 'algorithm': 'ball_tree'}, {'n_neighbors': 3, 'algorithm': 'ball_tree'}, {'n_neighbors': 2, 'algorithm': 'brute'}, {'n_neighbors': 9, 'algorithm': 'kd_tree'}, {'n_neighbors': 5, 'algorithm': 'ball_tree'}, {'n_neighbors': 5, 'algorithm': 'kd_tree'}, {'n_neighbors': 2, 'algorithm': 'auto'}, {'n_neighbors': 5, 'algorithm': 'auto'}, {'n_neighbors': 10, 'algorithm': 'kd_tree'}, {'n_neighbors': 9, 'algorithm': 'ball_tree'}]
[0.72566667 0.66933333 0.66966667 0.66933333 0.774      0.774
 0.66966667 0.774      0.66133333 0.66933333]

    我们这里可以看到在选择迭代次数为 10 次的情况下，也选到了最高得分0.774，只不过不是相同的组合。

  • 随机搜索RandomizedSearchCV的一个主要问题就是无法保证找到全局最优的参数组合。

    随机搜索相比均匀搜索GridSearchCV主要有以下局限性:

  • 随机搜索仅依赖于随机抽样,每次抽样的结果都可能不同,无法系统性地探索整个搜索空间。

  • 它无法给出最优参数组合的保证,找到的结果仅是局部最优,可能误导进一步研究。

  • 对于参数空间较大或模型复杂度高的情况,随机搜索难以快速收敛到真正优解。

  • 搜索效率高得来的代价就是精度不能保证。随着n_iter增加,效果收敛是极慢的。

  • 参数空间较小,初步评估模型性能的任务
  • 计算资源十分紧张,需要快速得到可行解的情况

四、 贝叶斯搜索

贝叶斯优化属于一类序列模型优化(SMBO)算法,其工作原理可以更详细地描述如下:

1.建立序列模型

使用已有观测数据(X1*:n*, f1*:n*)建立一个序列模型M,用来拟合和预测损失函数f。序列模型通常采用高斯过程等贝叶斯非参数模型。

2.计算后验分布

根据序列模型M和观测数据,计算损失函数f在每一点X的后验分布p(f|X,D)。

3.确定下一个抽样点

从后验分布中利用acq函数选择下一个最有信息的点,比如选择期望改进加上不确定性的点(EIacquisition function)

4.迭代抽样评估

在确定的点X上评估真实损失f,并将新数据纳入D,重复上述过程迭代搜索。

5.收敛最优解

通过学习性地逼近全局最优点,迭代收敛找到全局或者局部最优解。

总之,SMBO通过建模历史数据来预测函数形式,选择有效的下一个试验点以最大程度提升收益,这是贝叶斯优化成功的关键。它充分利用先验信息对搜索空间进行有针对性的探索。

 

安装: pip install scikit-optimize
安装: pip install bayesian-optimization
两个库都可以实现
from skopt import BayesSearchCV

import warnings
warnings.filterwarnings("ignore")

# parameter ranges are specified by one of below
from skopt.space import Real, Categorical, Integer

knn = KNeighborsClassifier()
#defining hyper-parameter grid
grid_param = { 'n_neighbors' : list(range(2,11)) , 
              'algorithm' : ['auto','ball_tree','kd_tree','brute'] }

#initializing Bayesian Search
Bayes = BayesSearchCV(knn , grid_param , n_iter=30 , random_state=14)
Bayes.fit(X_train,y_train)

#best parameter combination
Bayes.best_params_

#score achieved with best parameter combination
Bayes.best_score_

#all combinations of hyperparameters
Bayes.cv_results_['params']

#average scores of cross-validation
Bayes.cv_results_['mean_test_score']

import warnings
warnings.filterwarnings("ignore")

 warnings模块可以控制Python代码执行过程中打印出来的警告信息。

然后,调用filterwarnings方法设置警告信息的打印模式:

warnings.filterwarnings("ignore")

这里设置为"ignore",意为忽略所有警告信息,不展示打印出来。

设置这个是为了清理输出,避免警告信息对结果产生干扰。

因为一些示例代码或教学代码中的警告可能不代表实际问题,打印出来会影响阅读。

但这只针对演示性代码,对于正式产品级代码,打印警告还是很重要的,可以发现潜在bug。

所以这两行设置的目的是,清理输出,专注于代码结果,忽略可能的非重要警告输出,使输出更加简洁明了。

它通过warnings模块控制Python默认打印警告的行为,实现了对警告信息的过滤。

注释掉之后确实会出来警告，没注释之前未出来这些警告 

OrderedDict([('algorithm', 'ball_tree'), ('n_neighbors', 5)])
0.774
[OrderedDict([('algorithm', 'brute'), ('n_neighbors', 2)]), OrderedDict([('algorithm', 'brute'), ('n_neighbors', 7)]), OrderedDict([('algorithm', 'kd_tree'), ('n_neighbors', 3)]), OrderedDict([('algorithm', 'auto'), ('n_neighbors', 2)]), OrderedDict([('algorithm', 'brute'), ('n_neighbors', 3)]), OrderedDict([('algorithm', 'brute'), ('n_neighbors', 7)]), OrderedDict([('algorithm', 'ball_tree'), ('n_neighbors', 5)]), OrderedDict([('algorithm', 'kd_tree'), ('n_neighbors', 8)]), OrderedDict([('algorithm', 'brute'), ('n_neighbors', 5)]), OrderedDict([('algorithm', 'brute'), ('n_neighbors', 8)]), OrderedDict([('algorithm', 'auto'), ('n_neighbors', 4)]), OrderedDict([('algorithm', 'brute'), ('n_neighbors', 9)]), OrderedDict([('algorithm', 'auto'), ('n_neighbors', 5)]), OrderedDict([('algorithm', 'brute'), ('n_neighbors', 6)]), OrderedDict([('algorithm', 'brute'), ('n_neighbors', 10)]), OrderedDict([('algorithm', 'brute'), ('n_neighbors', 7)]), OrderedDict([('algorithm', 'kd_tree'), ('n_neighbors', 5)]), OrderedDict([('algorithm', 'auto'), ('n_neighbors', 5)]), OrderedDict([('algorithm', 'ball_tree'), ('n_neighbors', 5)]), OrderedDict([('algorithm', 'brute'), ('n_neighbors', 5)]), OrderedDict([('algorithm', 'brute'), ('n_neighbors', 7)]), OrderedDict([('algorithm', 'kd_tree'), ('n_neighbors', 5)]), OrderedDict([('algorithm', 'ball_tree'), ('n_neighbors', 5)]), OrderedDict([('algorithm', 'auto'), ('n_neighbors', 8)]), OrderedDict([('algorithm', 'auto'), ('n_neighbors', 5)]), OrderedDict([('algorithm', 'ball_tree'), ('n_neighbors', 8)]), OrderedDict([('algorithm', 'kd_tree'), ('n_neighbors', 5)]), OrderedDict([('algorithm', 'brute'), ('n_neighbors', 4)]), OrderedDict([('algorithm', 'brute'), ('n_neighbors', 5)]), OrderedDict([('algorithm', 'auto'), ('n_neighbors', 4)])]
[0.66966667 0.72566667 0.66933333 0.66966667 0.66933333 0.72566667
 0.774      0.71766667 0.774      0.71766667 0.70966667 0.66933333
 0.774      0.70966667 0.66133333 0.72566667 0.774      0.774
 0.774      0.774      0.72566667 0.774      0.774      0.71766667
 0.774      0.71766667 0.774      0.70966667 0.774      0.70966667]

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/914093.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

2023-8-22 模拟队列

2023-8-22 模拟队列

题目链接&#xff1a;模拟队列 #include <iostream>using namespace std;const int N 100010;int m; int q[N], hh, tt -1;int main() {cin >> m;while(m--){string op;int x;cin >> op;if(op "push"){cin >> x;q[tt] x;}else if(op …
阅读更多...
原型链继承的缺点

原型链继承的缺点

记录一下原型链继承的缺点&#xff1a; 第一点是实例共享属性的问题&#xff0c;如果实例改变了继承的引用类型属性&#xff0c;那么其他实例属性也会被改变 第二点是实例对象的 constructor 属性不正确。child 的 constructor 属性并未指向它自己的构造函数 继承代码如下 …
阅读更多...
【水平垂直居中布局】CSS实现水平垂直居中的5种方法（附源码）

【水平垂直居中布局】CSS实现水平垂直居中的5种方法（附源码）

文章目录 写在前面涉及知识点1、子绝对定位父相对定位&#xff0c;子节点设置位移实现1.1效果1.2实现源码 2、子绝对定位父相对定位&#xff0c;子节点设置上下边距2.1 效果2.2 实现源码 3、利用flex布局实现3.1 效果3.2 实现源码 4、利用行高和文本水平居中设置4.1 效果4.2 实…
阅读更多...
Python代码实现天天酷跑小游戏

Python代码实现天天酷跑小游戏

前言 最近几天多给大家分享分享一些用Python代码&#xff0c;写出来的小游戏吧 今天分享的游戏是 天天酷跑 大概的效果是这样的&#xff0c;动图没展示出来&#xff0c;大家将就看一下吧 【源码的话 文末名片可以获取 】 实现代码 定义 import pygame,sys import random游…
阅读更多...
win11查看文件/文件夹所使用的程序

win11查看文件/文件夹所使用的程序

CtrlShiftEsc 打开任务管理器 打开资源管理器 搜索文件名 右击结束进程
阅读更多...
【力扣】374、猜数字大小

【力扣】374、猜数字大小

猜数字游戏的规则如下&#xff1a; 每轮游戏&#xff0c;我都会从 1 到 n 随机选择一个数字。 请你猜选出的是哪个数字。 如果你猜错了&#xff0c;我会告诉你&#xff0c;你猜测的数字比我选出的数字是大了还是小了。 你可以通过调用一个预先定义好的接口 int guess(int num)…
阅读更多...
第七章，文章界面

第七章，文章界面

7.1添加个人专栏 <template><div class="blog-container"><div class="blog-pages"><!-- 用于渲染『文章列表』和『文章内容』 --><router-view/><div class="col-md-3 main-col pull-left"><div cla…
阅读更多...
STL list基本用法

STL list基本用法

目录 list的使用构造函数和赋值重载迭代器(最重要)容量相关插入删除元素操作reversesortuniqueremovesplice list的底层实际是双向链表结构 list的使用 构造函数和赋值重载 构造函数说明list()无参构造list (size_type n, const value_type& val value_type())构造的li…
阅读更多...
docker 部署服务

docker 部署服务

1、使用mysql:5.6和 owncloud 镜像&#xff0c;构建一个个人网盘。 [rootbogon ~]# docker pull mysql:5.6 [rootbogon ~]# docker pull owncloud [rootbogon ~]# docker run -itd --name mysql --env MYSQL_ROOT_PASSWORD123456 mysql:5.6 [rootbogon ~]# docker run -itd -…
阅读更多...
SeLinux权限说明及问题解决

SeLinux权限说明及问题解决

一、SELinux文件访问安全策略和app权限配置 在android6.0以后的版本&#xff0c;google采用了SELinux的文件访问安全策略&#xff0c;想比较以前&#xff0c;绝对提高了文件的安全&#xff0c;不像以前那样&#xff0c; 对文件访问可以是无条件的。本篇文章就分享下常用的一些…
阅读更多...
走进大模型

走进大模型

1、应用大模型 AIGC 是基于大模型的&#xff0c;而大模型的基础是深度学习。上一篇文章对深度学习进行了初步介绍&#xff0c;首先是深度学习的神经元起源&#xff0c;引发了基于线性函数的模拟&#xff0c;又因为线性函数无法习得逻辑异或&#xff0c;因此引入了非线性的激活…
阅读更多...
Linux系统常用指令

Linux系统常用指令

目录 1.帮助指令 2.文件目录指令* 3.查找指令 4.时间日期指令 5.压缩和解压 1.帮助指令 ctrl c 取消命令&#xff0c;并且换行&#xff08;清空换行&#xff09;作用&#xff0c;单独清空为crtl u tab换行键 补全命令和文件名&#xff0c;快速按两下可以显示备选选项 …
阅读更多...
kafka-python 消费者消费不到消息

kafka-python 消费者消费不到消息

排除步骤1&#xff1a; 使用group_id”consumer_group_id_001“ 和 auto_offset_reset"earliest" from kafka import KafkaConsumerconsumer KafkaConsumer(bootstrap_servers["dev-kafka01.test.xxx.cloud:9092"],enable_auto_commitTrue, auto_commit…
阅读更多...
arm: day8

arm: day8

1.中断实验&#xff1a;按键控制led灯 流程&#xff1a; key.h /*************************************************************************> File Name: include/key.h> Created Time: 2023年08月21日 星期一 17时03分20秒***************************************…
阅读更多...
02-Flask框架和项目启动

02-Flask框架和项目启动

安装Flask 1. 使用pycharm 企业版,直接选择Flask 2. 手动安装 (1) 进入终端进入虚拟环境 执行 pip list ,查看虚拟环境已安装的已三方库 (2) 手动安装Flask第三方库 pip install flask2.0.2 -i https://pypi.tuna.tsinghua.edu.cn/simple/ (3) 安装 pymysl ,和数据库关联第三…
阅读更多...
HexoAssistant——博客上传助手(含源码)

HexoAssistant——博客上传助手(含源码)

文章目录 HexoAssistant——博客上传助手(含源码)1 前言2 效果演示3 源码地址4 总结 HexoAssistant——博客上传助手(含源码) 1 前言 旅行之余&#xff0c;用PyQt5写了一个博客上传的工具&#xff0c;旨在更加便捷地将本地文章上传Github博客。之前虽然配置过hexogithub的博客…
阅读更多...
2023-8-22 模拟栈

2023-8-22 模拟栈

题目链接&#xff1a;模拟栈 #include <iostream>using namespace std;const int N 100010;int m; int stk[N], tt;int main() {cin >> m;while(m--){string op;int x;cin >> op;if(op "push") {cin >> x;stk[tt] x;}else if(op "…
阅读更多...
浅入深出充分理解--＞(fork())父子进程

浅入深出充分理解--＞(fork())父子进程

目录 进程是如何被管理的 Linux下的进程是如何被管理的 fork()父子进程的创建 1&#xff1a;为什么fork返回给父进程子进程的id&#xff0c;给子进程返回0 2&#xff1a;一个函数是如何做到返回两次的 3&#xff1a;一个变量怎么会有不同内容 在某一个时刻,我正在用电脑打…
阅读更多...
【Unity3D】水面特效

【Unity3D】水面特效

1 前言 水波特效 中通过屏幕后处理实现了环形水波效果&#xff0c;本文通过 Shader Graph 实现了模拟水面特效&#xff0c;包含以下特效细节。 深水区和浅水区颜色差异&#xff1b;水面有波纹&#xff0c;并且在移动&#xff1b;水面起伏波动&#xff1b;水面边缘有水泡&#…
阅读更多...
《数字图像处理-OpenCV/Python》连载（1）前言

《数字图像处理-OpenCV/Python》连载（1）前言

《数字图像处理-OpenCV/Python》连载&#xff08;1&#xff09;前言 本书京东优惠购书链接&#xff1a;https://item.jd.com/14098452.html 写作背景 编写本书的初衷&#xff0c;源自作者学习数字图像处理的经历。 在创新实验班开设的专业创新教育课程中&#xff0c;我选择的…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023