欢迎关注更多精彩
关注我,学习常用算法与数据结构,一题多解,降维打击。
题目大意
http://acm.hdu.edu.cn/showproblem.php?pid=6097
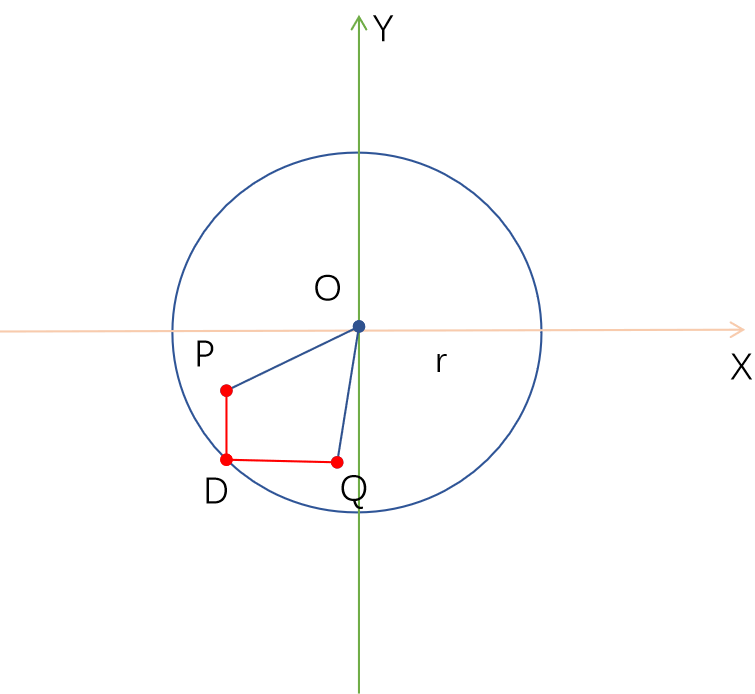
有一个圆C,它的圆心是O(0,0), 半径是r。
在C内部或边界上有两点P和Q,OP=OQ。
求解圆C上一点D,使得PD+QD最小。图中红色相加最短。
错解
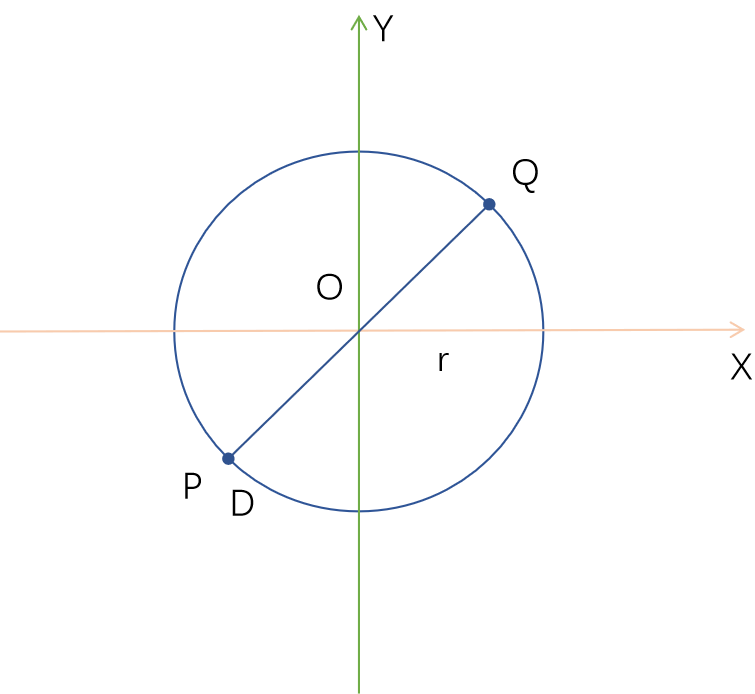
直觉上感觉D是PQ中垂线与圆的交点。
这个直觉是错误的。
一个特殊例子,当PQ是直径时,显然D点是P或Q时取得最值。
利用圆的反演及相似三角形转化圆外点问题
反演定义:有一个圆C以O为圆心半径为r,那么任意点P对于圆C的反演点P'存在于射线OP方向上,且OP' = r*r/OP
寻找相似三角形
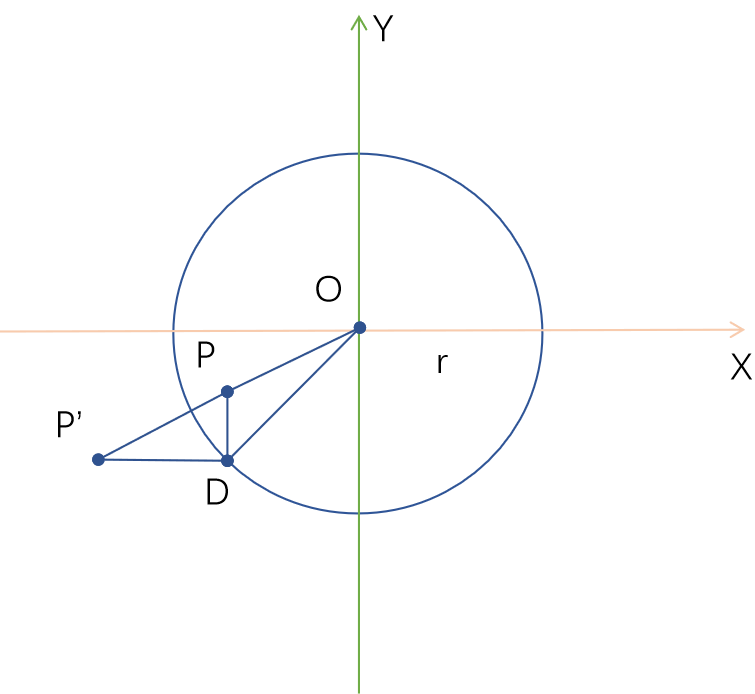
图中P’是P关于圆O的反演点。
则存在圆上
1
点
D
使得
△
P
′
D
O
∼
△
D
P
O
相似比为
r
O
P
则存在圆上1点D使得 \triangle P'DO \sim \triangle DPO 相似比为\frac {r}{OP}
则存在圆上1点D使得△P′DO∼△DPO相似比为OPr
证明也很简单:
根据已知条件,P’是P的反演点可得到
OP’ = r*r/OP => OP’/r=r/OP = OD/OP
根据两边之比相等且夹角相等,可以得到上述相似三角形的结论。
问题转化
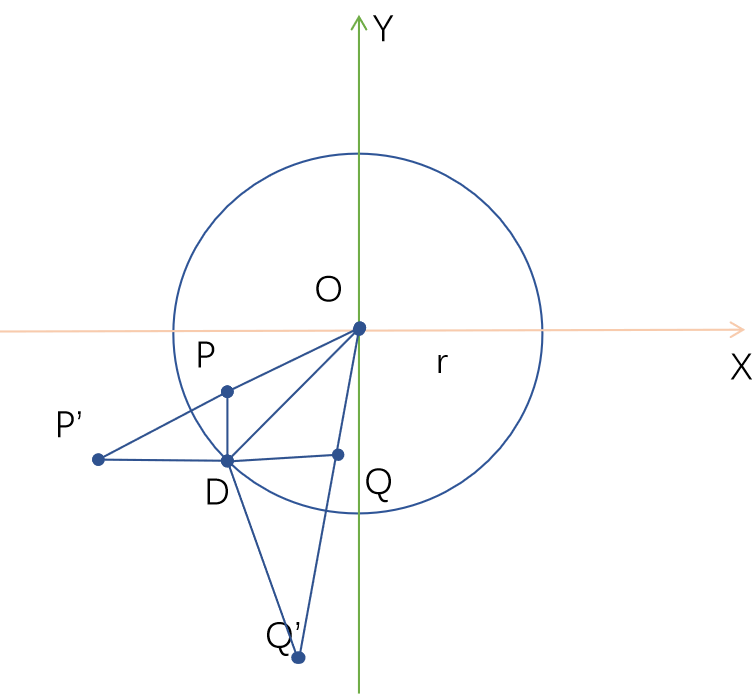
根据上述结论,Q’D/DQ=P’D/DP=r/OP(已知量)
得到
Q
′
D
+
P
′
D
D
Q
+
D
P
=
r
O
P
\frac {Q'D+P'D}{DQ+DP} = \frac {r}{OP}
DQ+DPQ′D+P′D=OPr
那么想要 DQ+DP 最小只要保证Q’D+P’D最小即可,问题就转化成求Q’D+P’D的最小值。
问题求解
对Q’和P’作边线可以发现下述两种情况。
相交
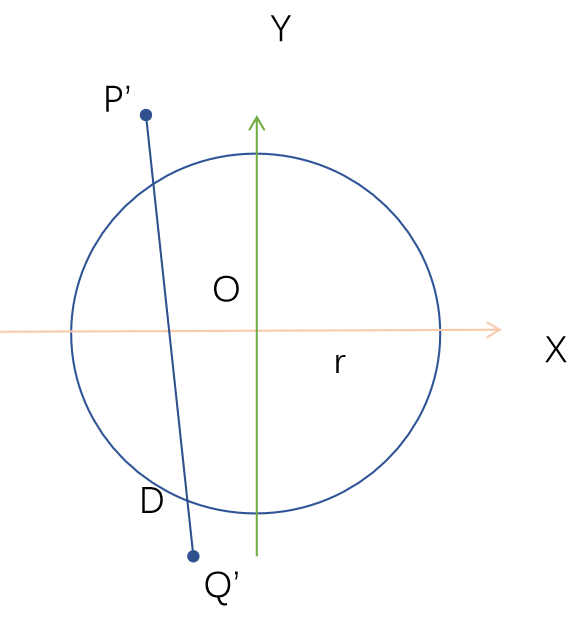
当与圆相交时,最短就是两点的连线,那么D就是圆上与连线的交点。
相离
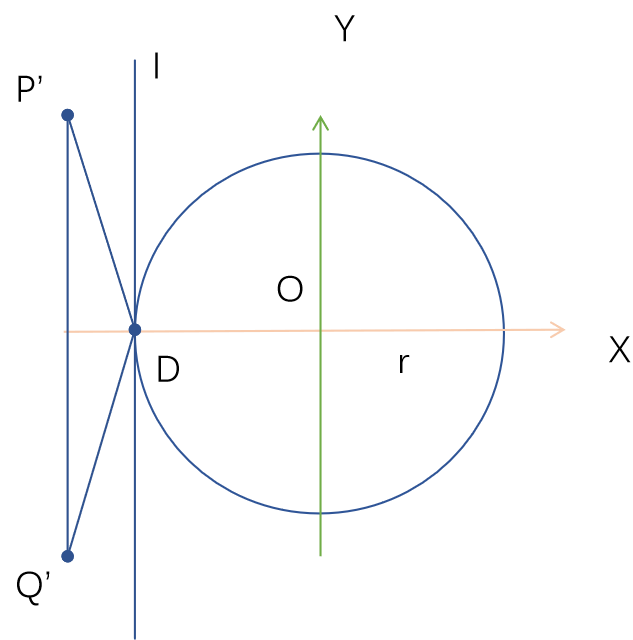
直觉D点是Q’P’中垂线与圆的交点。
证明如下:
假设Q’P’平等于Y轴,引入辅助线l平行于Q’P’与圆相切。
设向量P’D=(x,-y), Q’D = (x,y), 引入变量y*表示D在直线l上移动。
距离之和可以表示为关于 y ∗ 的函数 f ( y ∗ ) = x 2 + ( − y + y ∗ ) 2 + x 2 + ( y + y ∗ ) 2 距离之和可以表示为关于y*的函数 f(y*) = \sqrt{x^2+(-y+y*)^2}+\sqrt{x^2+(y+y*)^2} 距离之和可以表示为关于y∗的函数f(y∗)=x2+(−y+y∗)2+x2+(y+y∗)2
对f(y*)求导等于0
f
′
(
y
∗
)
=
−
y
+
y
∗
x
2
+
(
−
y
+
y
∗
)
2
+
y
+
y
∗
x
2
+
(
y
+
y
∗
)
2
f'(y*) = \frac {-y+y*}{\sqrt{x^2+(-y+y*)^2}}+\frac {y+y*}{\sqrt{x^2+(y+y*)^2}}
f′(y∗)=x2+(−y+y∗)2−y+y∗+x2+(y+y∗)2y+y∗
当y*=0时,f’(y*)=0。
在圆上移动会比直线上更远。
上述结论得证。
如何求P’D+Q’D。
设P’Q’中点为M, 则DM = OM-r。
根据勾股定理可求得P’D。
代码实现
#include<stdio.h>
#include<cmath>
class Point {
public:
double x, y;
Point() {}
Point(double a, double b) :x(a), y(b) {}
void in() {
scanf(" %lf %lf", &x, &y);
}
double dis() {
return sqrt(x * x + y * y);
}
void operator -=(Point& p) {
x -= p.x;
y -= p.y;
}
void operator +=(Point& p) {
x += p.x;
y += p.y;
}
void operator *=(double d) {
x *= d;
y *= d;
}
void operator /=(double d) {
this ->operator*= (1 / d);
}
};
class Circle
{
public:
Point center;
double r;
Circle(Point &c, double a):center(c), r(a){}
Circle();
void in() {
center.in();
scanf("%lf", &r);
}
};
Circle::Circle()
{
}
void solve() {
Point P, Q, P1, Q1, M;
int T;
Circle c;
scanf("%d", &T);
while (T--) {
scanf("%lf", &c.r);
c.center = Point(0, 0);
int a, b;
scanf("%d %d", &a, &b);
P.x = a;
P.y = b;
scanf("%d %d", &a, &b);
Q.x = a;
Q.y = b;
if (P.dis() < 1e-6) {
printf("%8f\n", 2*c.r);
continue;
}
// 求反演点
double k = c.r * c.r / P.dis() / P.dis();
P1 = P;
P1 *= k;
Q1 = Q;
Q1 *= k;
// 计算中点
M = P1;
M += Q1;
M /= 2;
P1 -= Q1;
double d = P1.dis();
// 判断相离情况
if (M.dis() > c.r) {
double md = M.dis() - c.r;
Q1 = Point(md, d/2);
d = Q1.dis() * 2;
}
d *= P.dis() / c.r;
printf("%.8f\n", d);
}
}
int main() {
solve();
return 0;
}
/*
4
4
4 0
0 4
4
0 3
3 0
4
0 2
2 0
4
0 1
1 0
*/
本人码农,希望通过自己的分享,让大家更容易学懂计算机知识。