669. 修剪二叉搜索树

文章目录

• • • [669. 修剪二叉搜索树](https://leetcode.cn/problems/trim-a-binary-search-tree/)
    • • 一、题目
      • 二、题解
      • • 方法一：递归法
        • 方法二：迭代法

---

一、题目

给你二叉搜索树的根节点 root ，同时给定最小边界low 和最大边界 high。通过修剪二叉搜索树，使得所有节点的值在[low, high]中。修剪树 不应该 改变保留在树中的元素的相对结构 (即，如果没有被移除，原有的父代子代关系都应当保留)。 可以证明，存在 唯一的答案 。

所以结果应当返回修剪好的二叉搜索树的新的根节点。注意，根节点可能会根据给定的边界发生改变。

示例 1：

输入：root = [1,0,2], low = 1, high = 2
输出：[1,null,2]

示例 2：

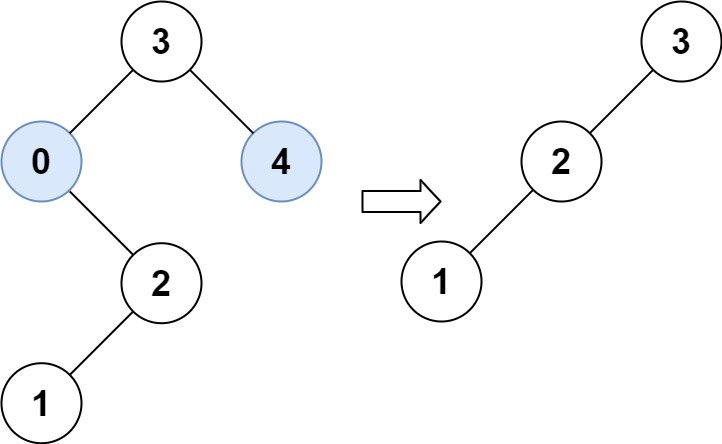
输入：root = [3,0,4,null,2,null,null,1], low = 1, high = 3
输出：[3,2,null,1]

提示：

• 树中节点数在范围 [1, 104] 内
• 0 <= Node.val <= 104
• 树中每个节点的值都是 唯一 的
• 题目数据保证输入是一棵有效的二叉搜索树
• 0 <= low <= high <= 104

二、题解

方法一：递归法

我们从根节点开始，逐个遍历树的节点，判断每个节点的值是否在给定的范围内。如果节点的值小于最小值（low），那么我们就需要修剪掉左子树，因为左子树的节点值都会更小，不可能在范围内。类似地，如果节点的值大于最大值（high），就需要修剪掉右子树。如果节点的值在范围内，我们保留这个节点，并分别递归修剪左子树和右子树。

下面是具体的算法思路以及解题步骤：

算法思路：

1. 如果树为空（即根节点为nullptr），直接返回nullptr，因为没有需要修剪的节点。
2. 如果根节点的值小于最小值low，那么根节点以及左子树的所有节点都会小于low，所以我们需要修剪掉左子树，递归调用trimBST(root->right, low, high)，返回修剪后的右子树作为新的根节点。
3. 如果根节点的值大于最大值high，那么根节点以及右子树的所有节点都会大于high，所以我们需要修剪掉右子树，递归调用trimBST(root->left, low, high)，返回修剪后的左子树作为新的根节点。
4. 如果根节点的值在范围内，我们保留这个节点，并分别递归修剪左子树和右子树，即root->left = trimBST(root->left, low, high);和root->right = trimBST(root->right, low, high);。
5. 最后返回修剪后的根节点。

具体实现：

class Solution {
public:
    TreeNode* trimBST(TreeNode* root, int low, int high) {
        if(root == nullptr) return nullptr;
        
        if(root->val < low){
            return trimBST(root->right, low, high);
        }
        if(root->val > high){
            return trimBST(root->left, low, high);
        }
        
        root->left = trimBST(root->left, low, high);
        root->right = trimBST(root->right, low, high);
        return root;
    }
};

算法分析：

• 时间复杂度：每个节点都被访问了一次，所以时间复杂度为O(N)，其中N是树中的节点数。
• 空间复杂度：递归调用的栈空间，最坏情况下（树完全不平衡），递归的深度可以达到N，所以空间复杂度为O(N)。

方法二：迭代法

算法思路：

1. 首先，处理根节点为空的情况。如果根节点为空，直接返回 nullptr，因为没有需要修剪的节点。
2. 然后，我们需要找到新的根节点，它的值应当在范围 [low, high] 内。通过迭代循环，将当前根节点移动到满足条件的位置。如果当前根节点的值小于 low，说明应当修剪掉左子树，所以移动到右子树；如果当前根节点的值大于 high，说明应当修剪掉右子树，所以移动到左子树。
3. 修剪左子树：从当前根节点开始，遍历到左子树的叶节点（最小值），如果叶节点的值小于 low，则将叶节点的右子树连接到当前叶节点的父节点上，从而删除小于 low 的节点。
4. 修剪右子树：从当前根节点开始，遍历到右子树的叶节点（最大值），如果叶节点的值大于 high，则将叶节点的左子树连接到当前叶节点的父节点上，从而删除大于 high 的节点。
5. 最后，返回修剪后的根节点。

具体实现：

class Solution {
public:
    TreeNode* trimBST(TreeNode* root, int low, int high) {
        if (!root) return nullptr;  // 处理根节点为空的情况

        // 找到新的根节点，值在 [low, high] 范围内
        while (root && (root->val < low || root->val > high)) {
            if (root->val < low)
                root = root->right;
            else
                root = root->left;
        }
        
        TreeNode *cur = root;

        // 修剪左子树
        while (cur && cur->left) {
            if (cur->left->val < low) {
                cur->left = cur->left->right;
            } else {
                cur = cur->left;
            }
        }

        cur = root;

        // 修剪右子树
        while (cur && cur->right) {
            if (cur->right->val > high) {
                cur->right = cur->right->left;
            } else {
                cur = cur->right;
            }
        }

        return root;
    }
};

算法分析：

• 时间复杂度：这个解法的时间复杂度取决于两个遍历操作。第一个遍历操作在找到新的根节点时，最多访问树中所有节点，所以是 O(N)。第二个和第三个遍历操作在修剪左右子树时，最多访问树中所有节点，也是 O(N)。综合起来，总的时间复杂度是 O(N)。
• 空间复杂度：这个解法没有使用额外的数据结构来存储中间结果，只使用了几个辅助变量，所以空间复杂度是 O(1)。