哈夫曼树
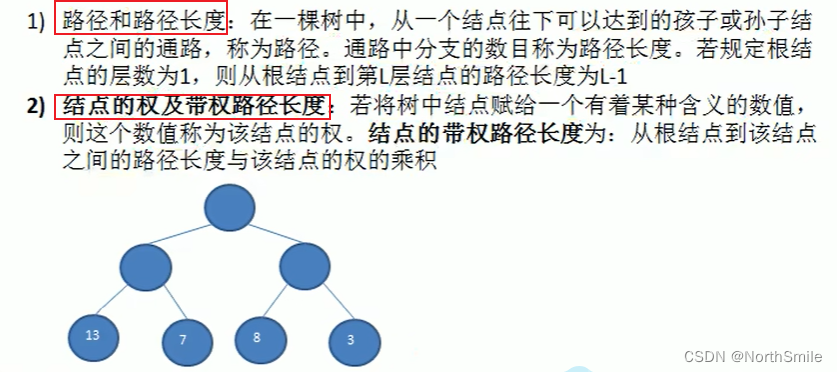
1. 介绍 1.1 哈夫曼树 1.2 路径、路径长度、结点的权、结点的带权路径长度 1.3 树的带权路径长度WPL 2. 哈夫曼树构建步骤 3. 代码实现
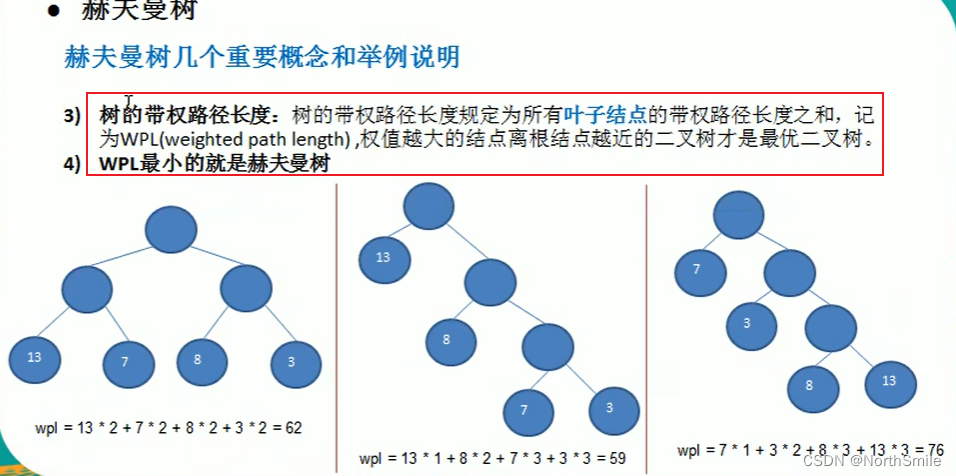
哈夫曼树-最优二叉树:树的带权路径长度最小的二叉树; 权值均为叶子结点; 权值越大,结点距离根节点越近;
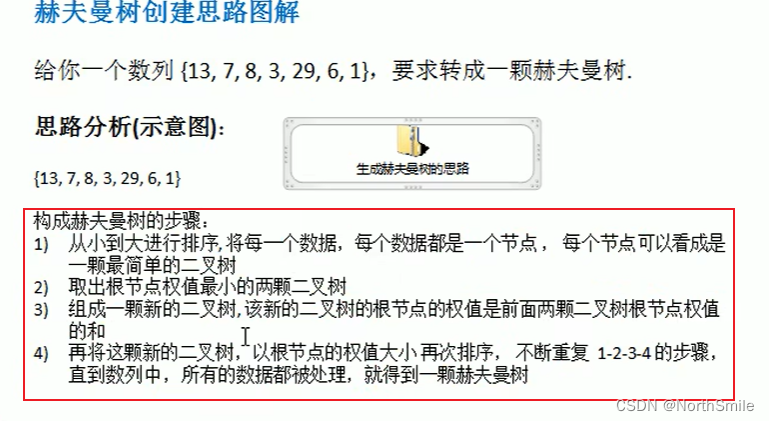
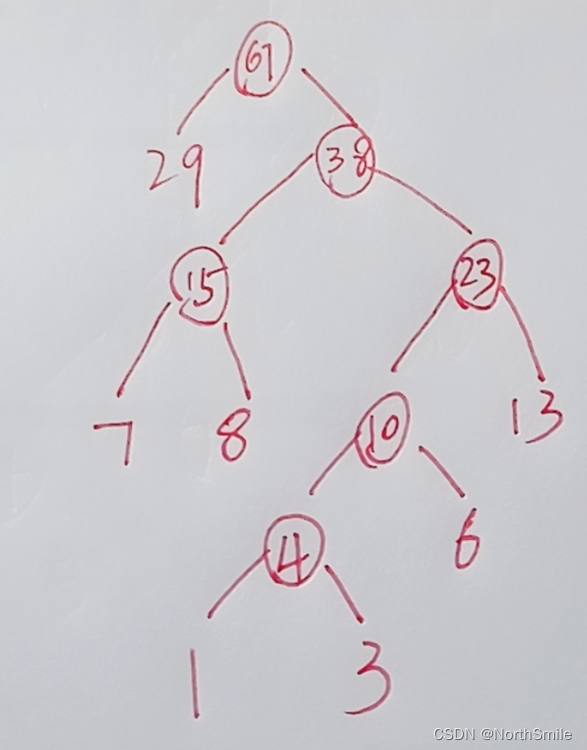
对权值序列进行升序排列,选出其中最小的两个权值进行合并; 将合并结点加入权值序列,重新进行排序; 重复执行上述两个操作,直到序列中只剩一个节点即可完成创建; 上述案例的手动构建结果: package com. northsmile. tree. huffman ;
import java. util. * ;
public class HuffmanTree {
public static void main ( String [ ] args) {
Scanner scanner= new Scanner ( System . in) ;
int n= Integer . parseInt ( scanner. nextLine ( ) ) ;
List < TreeNode > = new LinkedList < > ( ) ;
for ( int i= 0 ; i< n; i++ ) {
nodes. add ( new TreeNode ( Integer . parseInt ( scanner. nextLine ( ) ) ) ) ;
}
root= createHuffmanTree ( nodes) ;
System . out. println ( calWPL ( ) ) ;
}
private static TreeNode root;
public static TreeNode createHuffmanTree ( List < TreeNode > ) {
while ( nodes. size ( ) != 1 ) {
nodes. sort ( new Comparator < TreeNode > ( ) {
@Override
public int compare ( TreeNode o1, TreeNode o2) {
return o1. val- o2. val;
}
} ) ;
TreeNode left= nodes. get ( 0 ) ;
TreeNode right= nodes. get ( 1 ) ;
TreeNode curRoot = new TreeNode ( left. val+ right. val) ;
curRoot. left= left;
curRoot. right= right;
nodes. add ( curRoot) ;
nodes. remove ( 0 ) ;
nodes. remove ( 0 ) ;
}
return nodes. get ( 0 ) ;
}
public static int calWPL ( ) {
int wpl= 0 ;
Deque < TreeNode > = new ArrayDeque < > ( ) ;
queue. offer ( root) ;
int height= 0 ;
while ( ! queue. isEmpty ( ) ) {
int size= queue. size ( ) ;
for ( int i= 0 ; i< size; i++ ) {
TreeNode cur = queue. pop ( ) ;
if ( cur. left== null && cur. right== null ) {
wpl+= ( cur. val* height) ;
}
if ( cur. left!= null ) {
queue. offer ( cur. left) ;
}
if ( cur. right!= null ) {
queue. offer ( cur. right) ;
}
}
height++ ;
}
return wpl;
}
private static class TreeNode {
public int val;
public TreeNode left;
public TreeNode right;
public TreeNode ( int val) {
this . val= val;
}
}
}