第五章：平衡二叉树

news2024/12/29 8:40:35

系列文章目录

文章目录

  • 系列文章目录
  • 前言
  • 1、平衡二叉树的介绍
    • 1.1 AVL树的概念
    • 1.2 AVL树的性质
  • 2、平衡二叉树的插入
    • 2.1 平衡二叉树的插入步骤
    • 2.2 平衡二叉树的旋转
      • 2.2.1 左单旋
      • 2.2.2 右单旋
      • 2.2.3 左右双旋
      • 2.2.4 右左双旋
  • 3、平衡二叉树的检验
  • 4、平衡二叉树的删除
  • 5、整体代码

前言

AVL是一种二叉搜索树，通过平衡因子来实现平衡。

1、平衡二叉树的介绍

1.1 AVL树的概念

二叉搜索树虽可以缩短查找的效率，但如果数据有序或接近有序二叉搜索树将退化为单支树，查找元素相当于在顺序表中搜索元素，效率低下。因此，两位俄罗斯的数学家G.M.Adelson-Velskii和E.M.Landis在1962年发明了一种解决上述问题的方法：当向二叉搜索树中插入新结点后，如果能保证每个结点的左右子树高度之差的绝对值不超过1(需要对树中的结点进行调整)，即可降低树的高度，从而减少平均搜索长度。

平衡二叉树：在一棵搜索二叉树中每个节点的左右子树的高度差的绝对值不超过1。左右子树的高度差被称为平衡因子**（平衡因子=右子树高度-左子树高度）。**若一颗平衡二叉树的节点个数为n，那么其高度为logN。

1.2 AVL树的性质

一棵AVL树或者是空树，或者是具有以下性质的二叉搜索树：

  1. 它的左右子树都是AVL树

  2. 左右子树高度之差(简称平衡因子)的绝对值不超过1(-1/0/1)

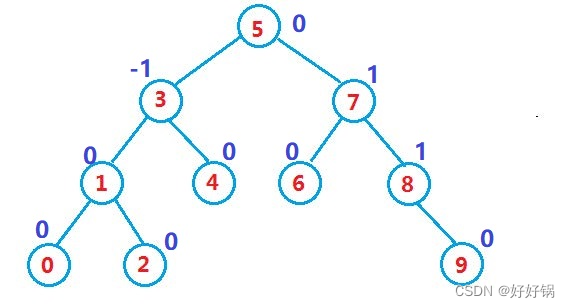
在这里插入图片描述

2、平衡二叉树的插入

2.1 平衡二叉树的插入步骤

平衡二叉树的插入第一步和二叉搜索树一样，根据二叉搜索树的特性，找到新插入节点位于整棵树的位置。

随后使用逻辑语句判断新节点是插入在父节点的左还是右，并维护其与父节点的指针关系。

新增在右，平衡因子++；新增在左，平衡因子–。那新插入了一个节点，原先的平衡二叉树的结构可能会遭到破坏（会影响插入节点的祖先的平衡因子），所以需要观察平衡因子的三种情况，进行分类讨论：如图

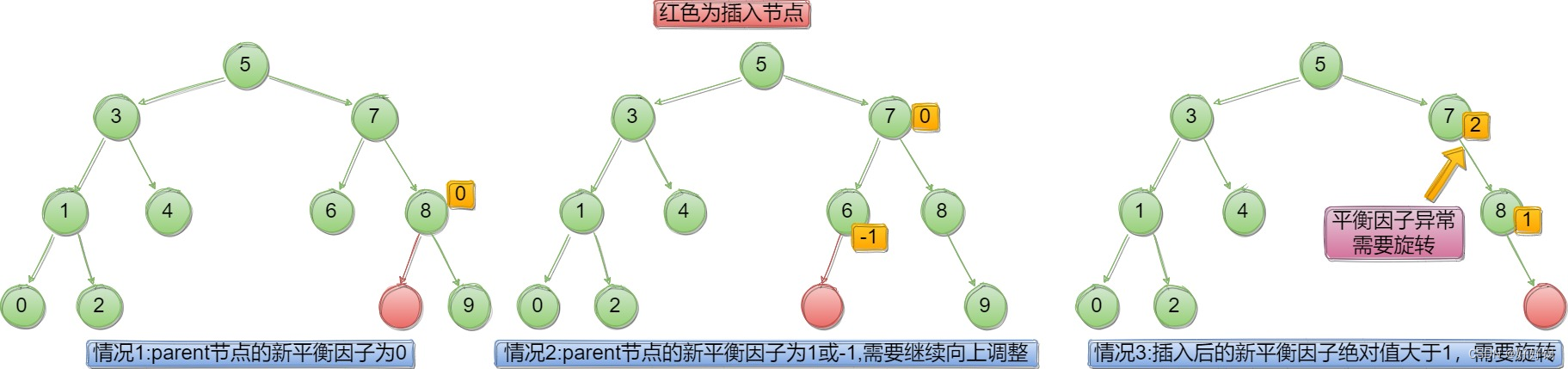
在这里插入图片描述

情况三如何旋转？无非是四种情况：

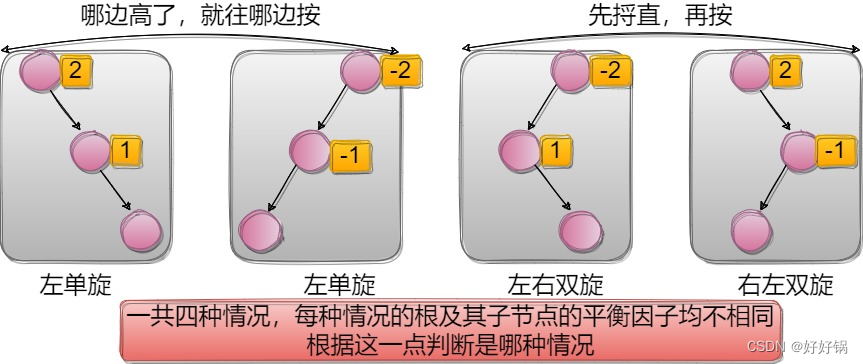
在这里插入图片描述

2.2 平衡二叉树的旋转

当出现上图情况三时，就需要对平衡二叉树的节点进行旋转，旋转的目的是要让这颗树继续维持平衡二叉树的形态，同时调节子树的高度，让其和插入前的高度保持一致，旋转后不要忘记更新那些被旋转的节点的平衡因子。

【旋转的原则】：保持它继续是搜索树。

【选择的目的】：1. 左右子树均衡；2. 同时调节子树的高度，让其和插入前的高度保持一致。

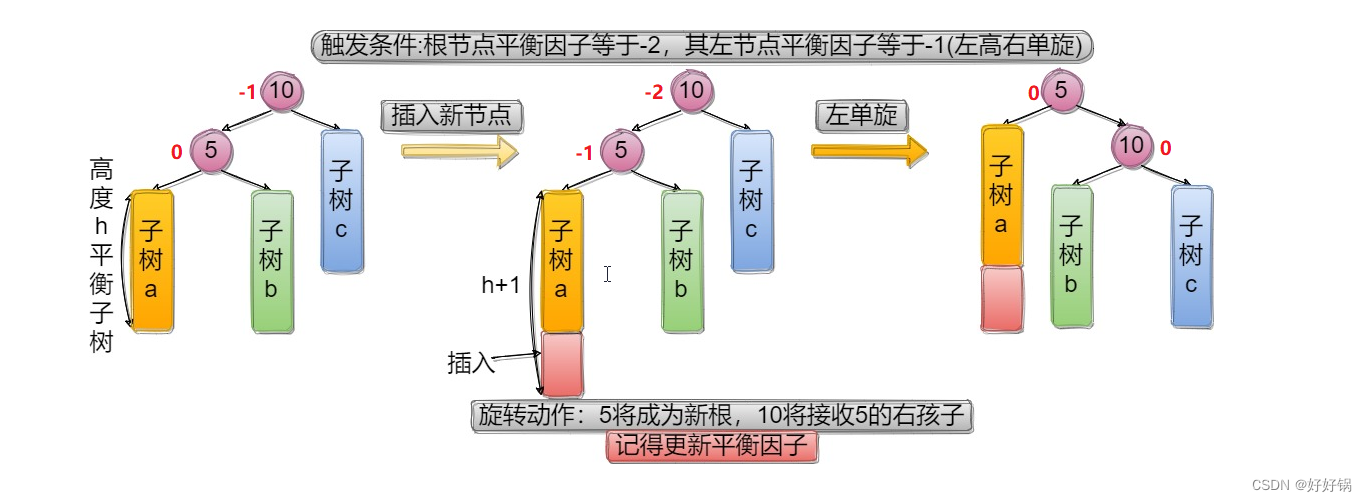
2.2.1 左单旋

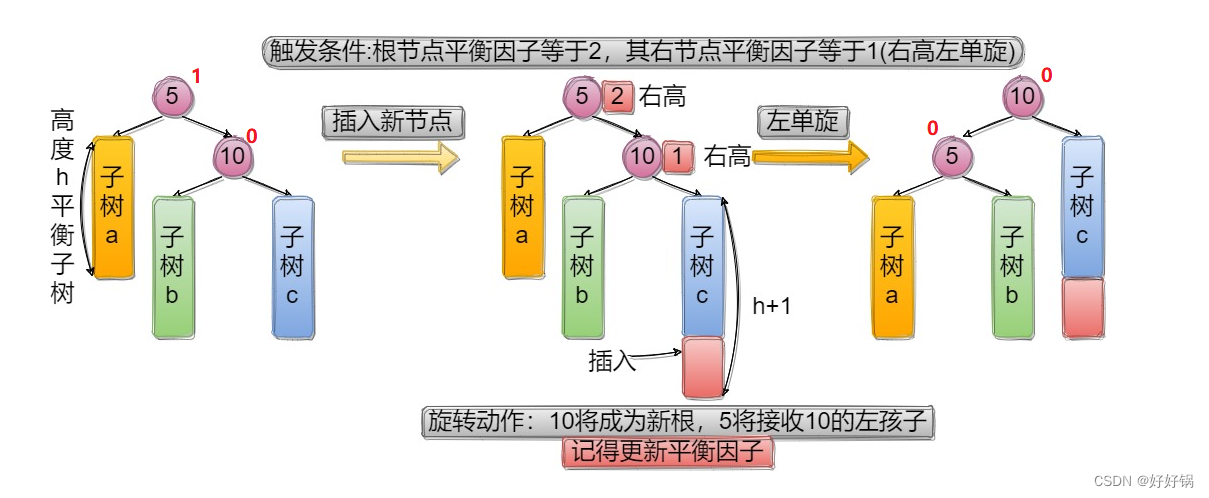
在这里插入图片描述

5可能是根，也可能是某颗子树的根，分类讨论：

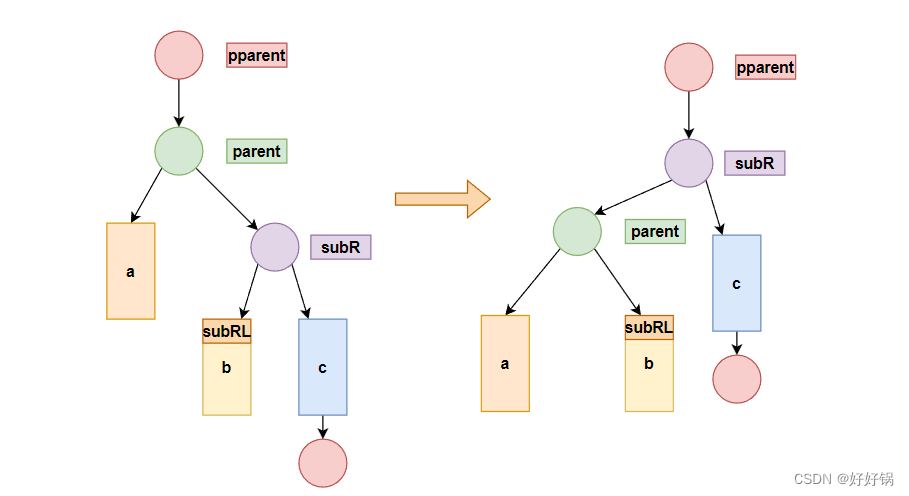
在这里插入图片描述

void RotateL(Node* parent)
{
    Node* subR = parent->_right;
    Node* subRL = subR->_left;

    parent->_right = subRL;
    if(subRL)
        subRL->_parent = parent;

    Node* ppnode = parent->_parent;

    subR->_left = parent;
    parent->_parent = subR;

    if (ppnode == nullptr)
    {
        _root = subR;
        _root->_parent = nullptr;
    }
    else
    {
        if (ppnode->_left == parent)
        {
            ppnode->_left = subR;
        }
        else
        {
            ppnode->_right = subR;
        }

        subR->_parent = ppnode;
    }

    parent->_bf = subR->_bf = 0;
}

2.2.2 右单旋

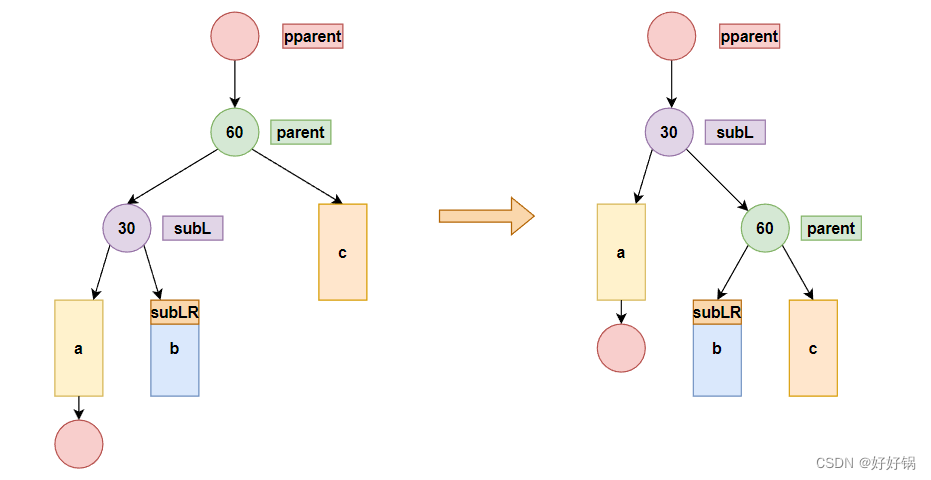
在这里插入图片描述

在这里插入图片描述

void RotateR(Node* parent)
{
    Node* subL = parent->_left;
    Node* subLR = subL->_right;

    parent->_left = subLR;
    if (subLR)
    {
        subLR->_parent = parent;
    }
    Node* ppnode = parent->_parent;

    subL->_right = parent;
    parent->_parent = subL;



    if (parent == _root)
    {
        _root = subL;
        _root->_parent = nullptr;
    }
    else
    {
        if (ppnode->_left == parent)
        {
            ppnode->_left = subL;
        }
        else
        {
            ppnode->_right = subL;

        }
        subL->_parent = ppnode;
    }

    parent->_bf = subL->_bf = 0;

}

2.2.3 左右双旋

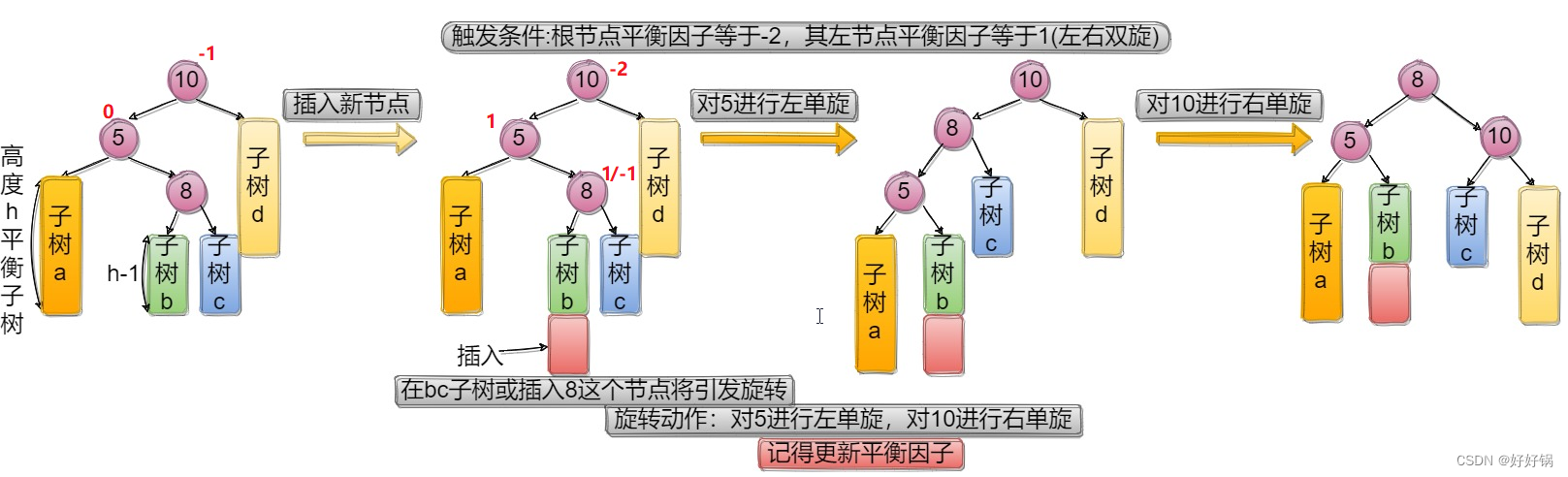
在这里插入图片描述

void RotateLR(Node* parent)
{
    Node* subL = parent->_left;
    Node* subLR = subL->_right;

    int bf = subLR->_bf;

    RotateL(parent->_left);
    RotateR(parent);

    if (bf == 1)
    {
        parent->_bf = 0;
        subLR->_bf = 0;
        subL->_bf = -1;
    }
    else if (bf == -1)
    {
        parent->_bf = 1;
        subLR->_bf = 0;
        subL->_bf = 0;
    }
    else if (bf == 0)
    {
        parent->_bf = 0;
        subLR->_bf = 0;
        subL->_bf = 0;
    }
    else
    {
        assert(false);
    }

}

2.2.4 右左双旋

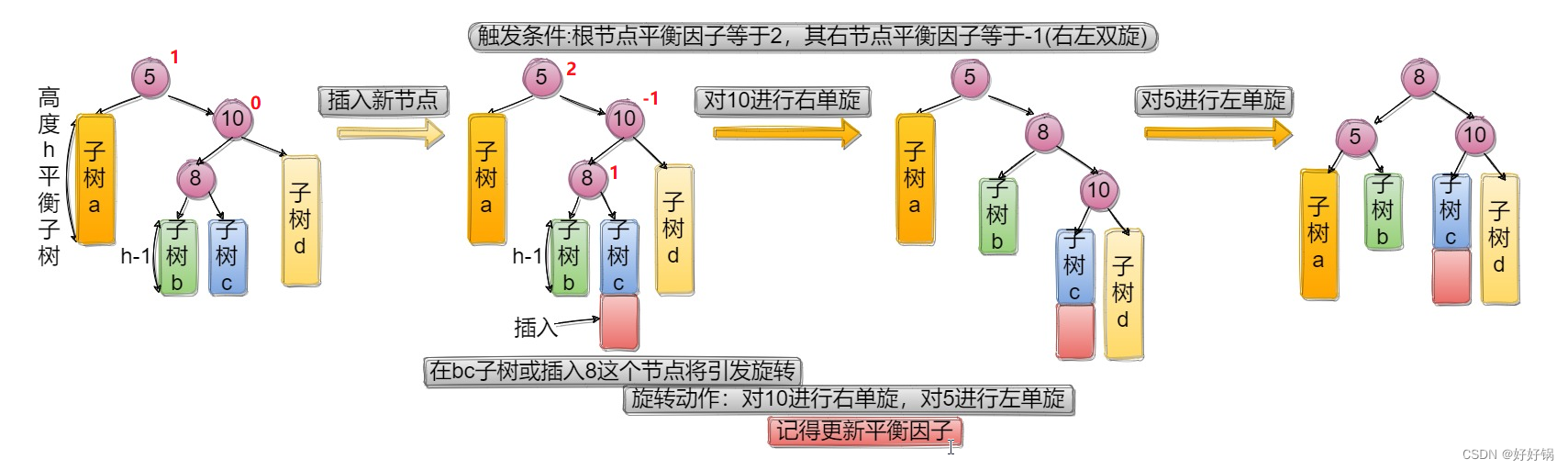
在这里插入图片描述

void RotateRL(Node* parent)
{
    Node* subR = parent->_right;
    Node* subRL = subR->_left;

    int bf = subRL->_bf;

    RotateR(parent->_right);
    RotateL(parent);

    if (bf == 1)
    {
        parent->_bf = -1;
        subRL->_bf = 0;
        subR->_bf = 0;
    }
    else if (bf == -1)
    {
        parent->_bf = 0;
        subRL->_bf = 0;
        subR->_bf = 1;
    }
    else if (bf == 0)
    {
        parent->_bf = 0;
        subRL->_bf = 0;
        subR->_bf = 0;
    }
    else
    {
        assert(false);
    }
}

3、平衡二叉树的检验

//求树的高度
int _Height(Node* root)
{
    if (root == nullptr)
        return 0;
    int leftH = _Height(root->_left);
    int rightH = _Height(root->_right);

    return leftH > rightH ? leftH + 1 : rightH + 1;
}

//判断是否是平衡树
bool _IsBalance(Node* root)
{
    if (root == nullptr)
    {
        return true;
    }

    int leftH = _Height(root->_left);
    int rightH = _Height(root->_right);

    //判断平衡因子
    if (rightH - leftH != root->_bf)
    {
        cout << root->_kv.first << "节点平衡因子异常" << endl;
        return false;
    }

    return abs(leftH - rightH) < 2
        && _IsBalance(root->_left)
        && _IsBalance(root->_right);

}

4、平衡二叉树的删除

按照二叉搜索树的方式对平衡二叉树节点进行删除。更新平衡因子时，平衡因子为1或-1便可以停止向上更新。当平衡因子绝对值大于1时，同样需要进行旋转解决。

5、整体代码

平衡二叉树强就强在通过大量的旋转控制整颗树任意一个节点的左右子树高度差不大于1，使树的结构近似完全二叉树，搜索效率为logN。

但偏偏是频繁的旋转，导致其插入删除的效率并不及红黑树，这也是红黑树成为树形容器的原因。

但是一颗树仅用来查找而不进行删除的话，用平衡二叉树还是很棒的。

#pragma once
#include <cassert>
#include <iostream>
#include <time.h>

using namespace std;

template <class K, class V>
struct AVLTreeNode
{
	AVLTreeNode<K, V>* _left;
	AVLTreeNode<K, V>* _right;
	AVLTreeNode<K, V>* _parent;
	pair<K, V> _kv;
	int _bf;//平衡因子

	AVLTreeNode(const pair<K, V>& kv)
		:_left(nullptr)
		,_right(nullptr)
		,_parent(nullptr)
		,_kv(kv)
		,_bf(0)
	{}
};

template<class K, class V>
class AVLTree
{
	typedef AVLTreeNode<K, V> Node;
public:
	bool Insert(const pair<K, V>& kv)
	{
		if (_root == nullptr)
		{
			_root = new Node(kv);
			return true;
		}
		Node* parent = nullptr;
		Node* cur = _root;
		while (cur)
		{
			if (cur->_kv.first > kv.first)
			{
				parent = cur;
				cur = cur->_left;
			}
			else if (cur->_kv.first < kv.first)
			{
				parent = cur;
				cur = cur->_right;
			}
			else
			{
				return false;
			}
		}

		cur = new Node(kv);

		if (parent->_kv.first > kv.first)
		{
			parent->_left = cur;
		}
		else
		{
			parent->_right = cur;
		}

		cur->_parent = parent;//链接父节点

		//更新平衡因子
		while (parent)
		{
			if (cur == parent->_right)
			{
				parent->_bf++;
			}
			else
			{
				parent->_bf--;
			}

			if (parent->_bf == 1 || parent->_bf == -1)
			{
				//继续更新
				parent = parent->_parent;
				cur = cur->_parent;
			}
			else if (parent->_bf == 0)
			{
				break;
			}
			else if (parent->_bf == 2 || parent->_bf == -2)
			{
				//旋转的原则：保持它继续是搜索树
				//选择的目的：左右均衡，降低整棵树的高度
				if (parent->_bf == 2 && cur->_bf == 1)
				{
					RotateL(parent);
				}
				else if (parent->_bf == -2 && cur->_bf == -1)
				{
					RotateR(parent);
				}
				else if(parent->_bf == -2 && cur->_bf == 1)
				{
					RotateLR(parent);
				}
				else if (parent->_bf == 2 && cur->_bf == -1)
				{
					RotateRL(parent);
				}
				else
				{
					assert(false);
				}

				break;
			}
			else
			{
				assert(false);
			}

		}

		return true;
	}

	//中序遍历
	void InOrder()
	{
		_InOrder(_root);
		cout << endl;
	}

	//判断是否是平衡二叉树
	bool IsBalance()
	{
		return _IsBalance(_root);
	}
	

private:
	//求树的高度
	int _Height(Node* root)
	{
		if (root == nullptr)
			return 0;
		int leftH = _Height(root->_left);
		int rightH = _Height(root->_right);

		return leftH > rightH ? leftH + 1 : rightH + 1;
	}

	//判断是否是平衡树
	bool _IsBalance(Node* root)
	{
		if (root == nullptr)
		{
			return true;
		}

		int leftH = _Height(root->_left);
		int rightH = _Height(root->_right);

		//判断平衡因子
		if (rightH - leftH != root->_bf)
		{
			cout << root->_kv.first << "节点平衡因子异常" << endl;
			return false;
		}

		return abs(leftH - rightH) < 2
			&& _IsBalance(root->_left)
			&& _IsBalance(root->_right);

	}

	//左旋转
	void RotateL(Node* parent)
	{
		Node* subR = parent->_right;
		Node* subRL = subR->_left;

		parent->_right = subRL;
		if(subRL)
			subRL->_parent = parent;

		Node* ppnode = parent->_parent;

		subR->_left = parent;
		parent->_parent = subR;

		if (ppnode == nullptr)
		{
			_root = subR;
			_root->_parent = nullptr;
		}
		else
		{
			if (ppnode->_left == parent)
			{
				ppnode->_left = subR;
			}
			else
			{
				ppnode->_right = subR;
			}

			subR->_parent = ppnode;
		}

		parent->_bf = subR->_bf = 0;
	}

	//右旋转
	void RotateR(Node* parent)
	{
		Node* subL = parent->_left;
		Node* subLR = subL->_right;

		parent->_left = subLR;
		if (subLR)
		{
			subLR->_parent = parent;
		}
		Node* ppnode = parent->_parent;

		subL->_right = parent;
		parent->_parent = subL;

		

		if (parent == _root)
		{
			_root = subL;
			_root->_parent = nullptr;
		}
		else
		{
			if (ppnode->_left == parent)
			{
				ppnode->_left = subL;
			}
			else
			{
				ppnode->_right = subL;
		
			}
			subL->_parent = ppnode;
		}

		parent->_bf = subL->_bf = 0;

	}

	//左右旋转
	void RotateLR(Node* parent)
	{
		Node* subL = parent->_left;
		Node* subLR = subL->_right;

		int bf = subLR->_bf;

		RotateL(parent->_left);
		RotateR(parent);

		if (bf == 1)
		{
			parent->_bf = 0;
			subLR->_bf = 0;
			subL->_bf = -1;
		}
		else if (bf == -1)
		{
			parent->_bf = 1;
			subLR->_bf = 0;
			subL->_bf = 0;
		}
		else if (bf == 0)
		{
			parent->_bf = 0;
			subLR->_bf = 0;
			subL->_bf = 0;
		}
		else
		{
			assert(false);
		}
			 
	}

	//右左旋转
	void RotateRL(Node* parent)
	{
		Node* subR = parent->_right;
		Node* subRL = subR->_left;

		int bf = subRL->_bf;

		RotateR(parent->_right);
		RotateL(parent);

		if (bf == 1)
		{
			parent->_bf = -1;
			subRL->_bf = 0;
			subR->_bf = 0;
		}
		else if (bf == -1)
		{
			parent->_bf = 0;
			subRL->_bf = 0;
			subR->_bf = 1;
		}
		else if (bf == 0)
		{
			parent->_bf = 0;
			subRL->_bf = 0;
			subR->_bf = 0;
		}
		else
		{
			assert(false);
		}
	}

	//中序遍历
	void _InOrder(Node* root)
	{
		if (root == nullptr)
		{
			return;
		}

		_InOrder(root->_left);
		cout << root->_kv.first << " ";
		_InOrder(root->_right);
	}


private:
	Node* _root = nullptr;
};

void Test_AVLTree1()
{//测试代码1
	//int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };
	int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };
	AVLTree<int, int> t1;
	for (auto e : a)
	{
		t1.Insert(make_pair(e, e));
		cout << e << ":" << t1.IsBalance() << endl;
	}

	t1.InOrder();
	cout << t1.IsBalance() << endl;
}

void Test_AVLTree2()
{//测试代码2
	srand(time(0));
	const size_t N = 5000000;
	AVLTree<int, int> t;
	for (size_t i = 0; i < N; ++i)
	{
		size_t x = rand() + i;
		t.Insert(make_pair(x, x));
		//cout << t.IsBalance() << endl;
	}

	//t.Inorder();

	cout << t.IsBalance() << endl;
	//cout << t.Height() << endl;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/910499.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Java并发编程第5讲——volatile关键字（万字详解）

Java并发编程第5讲——volatile关键字（万字详解）

volatile关键字大家并不陌生&#xff0c;尤其是在面试的时候&#xff0c;它被称为“轻量级的synchronized”。但是它并不容易完全被正确的理解&#xff0c;以至于很多程序员都不习惯去用它&#xff0c;处理并发问题的时候一律使用“万能”的sychronized来解决&#xff0c;然而如…
阅读更多...
Postman如何做接口自动化测试？

Postman如何做接口自动化测试？

前言 什么是自动化测试 把人对软件的测试行为转化为由机器执行测试行为的一种实践。 例如GUI自动化测试&#xff0c;模拟人去操作软件界面&#xff0c;把人从简单重复的劳动中解放出来。 本质是用代码去测试另一段代码&#xff0c;属于一种软件开发工作&#xff0c;已经开发完…
阅读更多...
v8引擎编译全过程

v8引擎编译全过程

环境vs2019 cmd 命令行需要设置成为代理模式 set http_proxyhttp://127.0.0.1:10809 set https_proxyhttp://127.0.0.1:10809 这个必须带上&#xff0c;不然报错&#xff0c;告诉编译器win系统的模式 set DEPOT_TOOLS_WIN_TOOLCHAIN0 源码 GitHub: GitHub - v8/v8: The…
阅读更多...
还不知道怎么提示LLM？ChatGPT提示入门

还不知道怎么提示LLM？ChatGPT提示入门

文章目录 简介&#xff1a;什么是人工智能&#xff1f;什么是提示过程&#xff1f;为什么会出现这样的差异&#xff1f; 为什么需要提示过程&#xff1f;1) 文章摘要2) 数学问题求解 如何进行提示过程&#xff1f;角色提示&#xff1a;多范例提示&#xff1a;无范例提示单范例提…
阅读更多...
糖尿病视网膜病灶分割（Diabetic Retinopathy Multi-lesion Segmentation）-RTNet论文总结

糖尿病视网膜病灶分割（Diabetic Retinopathy Multi-lesion Segmentation）-RTNet论文总结

论文&#xff1a;RTNet: Relation Transformer Network for Diabetic Retinopathy Multi-lesion Segmentation 目录 一、背景和出发点 二、创新点 三、方法实现 A. 概述 B. 全局transformer模块&#xff08;GTB&#xff09; C. 关系transformer模块&#xff08;RTB&#…
阅读更多...
【Linux操作系统】深入探索Linux系统编程中的信号集操作函数

【Linux操作系统】深入探索Linux系统编程中的信号集操作函数

在Linux系统编程中&#xff0c;信号集操作函数是非常重要的工具&#xff0c;它们允许我们对信号进行管理和控制。本篇博客将详细介绍Linux系统编程中的信号集操作函数&#xff0c;包括信号集的创建、添加和删除信号&#xff0c;以及对信号集进行操作的常用函数。通过深入了解这…
阅读更多...
华为Atlas的迭代关系、性能特点与典型应用场景

华为Atlas的迭代关系、性能特点与典型应用场景

衔接上文&#xff0c;本篇主要讲解华为Atlas训练卡的迭代关系。以及迭代后的训练卡性能特点与典型应用场景。 Atlas 300T A2 训练卡的迭代关系为Atlas 300T Pro升级到Atlas 300T A2。相比之下&#xff0c;Atlas 300T A2 性能特点&#xff1a; ○ 高度集成 AI算力、通用算力、…
阅读更多...
无人机巡检输电线路是什么，怎么巡？

无人机巡检输电线路是什么，怎么巡？

在今日科技迅速发展的时代&#xff0c;无人机为输电线路巡检提供了一种高效、安全且准确的解决方案。那么&#xff0c;为什么无人机巡检输电线路如此关键呢&#xff1f;以下是对这一问题的深入剖析。 1. 提高工作效率 传统的巡检模式与现实挑战&#xff1a;在过去&#xff0c;输…
阅读更多...
shell脚本语句（画矩形、三角形、乘法表和小游戏）(#^.^#)

shell脚本语句（画矩形、三角形、乘法表和小游戏）(#^.^#)

目录 一、语句 一、条件语句 一、以用户为例演示 一、显示当前登录系统的用户信息 二、显示有多少个用户 二、单分支if 一、输入脚本 二、验证结果 三、双分支if 一、输入脚本 二、验证结果 四、多分支if 一、输入脚本 二、验证 二、循环语句 一、shell版本的循环…
阅读更多...
【Freertos基础入门】深入浅出信号量

【Freertos基础入门】深入浅出信号量

文章目录 前言一、Freertos的信号量是什么&#xff1f;二、二进制信号量和计数型信号量是什么&#xff1f;三、信号量初步了解1.二进制信号量的使用2.give和take是什么&#xff1f;3.为什么需要动态和静态创建的方式&#xff1f; 四、二进制信号量示例代码总结 前言 本系列基于…
阅读更多...
docker之镜像与数据卷

docker之镜像与数据卷

镜像 简介 1.镜像是一种轻量级、可执行的独立软件包&#xff0c;用来打包软件运行环境和基于环境开发的软件&#xff0c;他包含运行某个软件所需的所有内容&#xff0c;包括代码、运行时库、环境变量、配置文件 2.将所有的应用和环境11&#xff0c;直接打包成docker镜像&…
阅读更多...
健康检测智能睡眠床垫方案

健康检测智能睡眠床垫方案

《2022中国睡眠质量调查报告》调查结果显示&#xff0c;16&#xff05;的被调查者存在夜间睡眠时间不足6个小时&#xff0c;表现为24点以后才上床睡觉&#xff0c;并且在6点之前起床&#xff1b;有83.81&#xff05;的被调查者经常受到睡眠问题困扰&#xff0c;其中入睡困难占2…
阅读更多...
文心一言 VS 讯飞星火 VS chatgpt （79）-- 算法导论7.4 4题

文心一言 VS 讯飞星火 VS chatgpt （79）-- 算法导论7.4 4题

四、请用go语言&#xff0c;证明:RANDOMIZED-QUICKSORT 期望运行时间是 Ω(nlgn)。 文心一言&#xff1a; 首先&#xff0c;为了证明RANDOMIZED-QUICKSORT的期望运行时间是Ω(nlg n)&#xff0c;我们需要证明在最坏的情况下&#xff0c;该算法的运行时间是O(nlg n)。然后&…
阅读更多...
无涯教程-PHP.INI File Configuration函数

无涯教程-PHP.INI File Configuration函数

PHP配置文件php.ini是影响PHP功能的最终且最直接的方法。每次初始化PHP时都会读取php.ini文件。换句话说,无论是模块版本的httpd重新启动还是CGI版本的每次脚本执行都重新启动。如果未显示您的更改,请记住停止并重新启动httpd。 该配置文件已注释完整。键区分大小写,关键字值不…
阅读更多...
阿里云服务器-修改ecs操作系统，把window系统更换成Linux操作系统

阿里云服务器-修改ecs操作系统，把window系统更换成Linux操作系统

其他sql格式也在更新中&#xff0c;可直接查看这个系列&#xff0c;要是没有你需要的格式&#xff0c;可在评论或私信我 总目录 目录-后期更新打算 hive的nvl中的子查询 总目录我这个是window&#xff0c;默认应该都是window&#xff0c;我需要改成Linux系统第一步&#xff…
阅读更多...
浅谈搭建CobaltStrike云服务器可能会遇到的一些问题

浅谈搭建CobaltStrike云服务器可能会遇到的一些问题

1.文件上传 若要将本机的文件上传至云服务器&#xff0c;你需通过Xshell来实现 先在xshell连接云服务器&#xff0c;命令行中执行rz命令&#xff0c;即可实现文件上传 若没有rz命令,则需用到以下命令进行安装(二选一): 适用于redhat linux: yum install lrzsz适用于centos或u…
阅读更多...
使用Mavon-Editor编辑器上传本地图片到又拍云云存储（Vue+SpringBoot）

使用Mavon-Editor编辑器上传本地图片到又拍云云存储（Vue+SpringBoot）

需求&#xff1a;将本地的图片上传到服务器或者云存储中&#xff0c;考虑之后&#xff0c;这里我选的是上传到又拍云云存储。 技术背景&#xff1a; 前端&#xff1a;VueAjax 后端&#xff1a;SpringBoot 存储&#xff1a;又拍云云存储原理&#xff1a;Mavon-Editor编辑器有两个…
阅读更多...
大模型框架LangChain开发实战（二）

大模型框架LangChain开发实战（二）

一、关于数据的准备及项目背景 Notion提供了团队管理的功能&#xff0c;方便团队成员进行在线协作办公&#xff0c;提高交互效率&#xff0c;notion上面的数据可能包括项目的数据&#xff0c;进度管理的数据&#xff0c;企业服务的数据等等&#xff0c;这里使用了从notion网站…
阅读更多...
【校招VIP】产品分析能力之用户画像出发

【校招VIP】产品分析能力之用户画像出发

考点介绍&#xff1a; 用户行为和交互是产品经理能力的重要部分&#xff0c;在校招中&#xff0c;基于用户画像的分析题和设计题也是高频考点。 『产品分析能力之用户画像出发』相关题目及解析内容可点击文章末尾链接查看&#xff01; 一、考点题目 1. 爱奇艺中搜索关键词“…
阅读更多...
【C++ 学习⑮】- 模板进阶

【C++ 学习⑮】- 模板进阶

目录 一、必须使用 typename 的场景 二、非类型模板参数 三、模板的特化 3.1 - 函数模板特化 3.2 - 类模板特化 3.2.1 - 全特化 3.2.2 - 偏特化 四、类模板分离式编译 4.1 - 分离编译的概念 4.2 - 类模板分离式的问题 4.3 - 解决方案 一、必须使用 typename 的场景 …
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023