目录
36.有效的数独
54.螺旋矩阵
48.旋转图像
73.矩阵置零
36.有效的数独
题意:
请你判断一个
9 x 9的数独是否有效。只需要 根据以下规则 ,验证已经填入的数字是否有效即可。
- 数字
1-9在每一行只能出现一次。- 数字
1-9在每一列只能出现一次。- 数字
1-9在每一个以粗实线分隔的3x3宫内只能出现一次。(请参考示例图)注意:
- 一个有效的数独(部分已被填充)不一定是可解的。
- 只需要根据以上规则,验证已经填入的数字是否有效即可。
- 空白格用
'.'表示。
【输入样例】
board = [["5","3",".",".","7",".",".",".","."] ,["6",".",".","1","9","5",".",".","."] ,[".","9","8",".",".",".",".","6","."] ,["8",".",".",".","6",".",".",".","3"] ,["4",".",".","8",".","3",".",".","1"] ,["7",".",".",".","2",".",".",".","6"] ,[".","6",".",".",".",".","2","8","."] ,[".",".",".","4","1","9",".",".","5"] ,[".",".",".",".","8",".",".","7","9"]]【输出样例】true
解题思路:
1. 按行和按列都比较简单,用一个二维数组a[i][num]来存储第i行/列中num出现的次数,num的取值范围是1~9;
2. 每个3×3的小九宫格,用三维数组来实现,matrix[i][j][num]表示的是三维数组中,第i行第j列这个九宫格中,num出现的次数。
3.观察九个小九宫格的坐标关系,最左上角的小九宫格的行列坐标范围是(0~2,0~2),如果将其除3,则坐标是(0,0),第二个九宫格(横着看)的坐标是(0~2,3~5),除3得到的结果是(0,1),因此,通过对行范围和列范围同时除3,可以将每个小九宫格在三维数组matrix中的坐标定下来(0,0),(0,1),(0,2),(1,0),(1,1),(1,2),(2,0),(2,1),(2,2)
4. ok,开始枚举,每次找到一个非"."的字符,就将其添加到三个统计数组中,添加完后要判断,加进去之后得到的a[i][num]的值会不会大于1,大于1表示不符合规律,列也一致。
class Solution {
public boolean isValidSudoku(char[][] board) {
int[][] row = new int[10][9];//行row[i][num]:第i行num值有多少个
int[][] col = new int[10][9];//列
int[][][] matrix = new int[10][10][9];//小矩阵
for(int i=0;i<9;++i){
for(int j=0;j<9;++j){
//先填充行的矩阵
char temp = board[i][j];
if(temp!='.'){
int num = temp - '0'-1;
++row[i][num];
++col[j][num];
++matrix[i/3][j/3][num];
if(row[i][num]>1||col[j][num]>1||matrix[i/3][j/3][num]>1){
return false;
}
}
}
}
return true;
}
}时间: 击败了18.26%
内存: 击败了5.14%
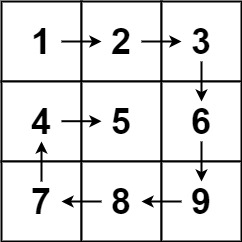
54.螺旋矩阵
题意:
给你一个
m行n列的矩阵matrix,请按照 顺时针螺旋顺序 ,返回矩阵中的所有元素。
【输入样例】
matrix=[[1,2,3],[4,5,6],[7,8,9]]
【输出样例】[1,2,3,6,9,8,7,4,5]
解题思路:
1. 首先,要有一个对应的标记矩阵isChoose[i][j],0表示matrix[i][j]中的值还没有遍历过;
2.定义行列访问指针i,j;根据题目规律,矩阵访问规律是:向右走-->向下走-->向左走-->向上走-->向右走
3. 定义变量count,用于统计已经访问多少数字了,方便结束循环;
class Solution {
public List<Integer> spiralOrder(int[][] matrix) {
//在有些题中也叫做蛇形矩阵
int m =matrix.length;//m行
int n = matrix[0].length;//n列
List<Integer> ans = new ArrayList<>();
if(matrix == null || m == 0 || n== 0){
return ans;
}
int i=0,j=0;
int[][] isChoose = new int[m][n];
isChoose[0][0] = 1;//从第一位开始,第一位先走
ans.add(matrix[0][0]);
int count = 1;
while(count < m*n){
//向右走,是列在变化,行不变
while(j+1 < n && isChoose[i][j+1] == 0){
//下一位没有越界,并且没有被访问过的时候,可以进行访问
ans.add(matrix[i][j+1]);
isChoose[i][j+1] = 1;
//统计个数
++count;
++j;
}
//向下走,行在变化
while(i+1 < m && isChoose[i+1][j] == 0){
//下一位没有越界,并且没有被访问过的时候,可以进行访问
ans.add(matrix[i+1][j]);
isChoose[i+1][j] = 1;
//统计个数
++count;
++i;
}
//向左走
while(j-1 >= 0 && isChoose[i][j-1] == 0){
//下一位没有越界,并且没有被访问过的时候,可以进行访问
ans.add(matrix[i][j-1]);
isChoose[i][j-1] = 1;
//统计个数
++count;
--j;
}
//向上走
while(i-1>= 0 && isChoose[i-1][j] == 0){
ans.add(matrix[i-1][j]);
isChoose[i-1][j] =1;
++count;
--i;
}
}
return ans;
}
}时间: 击败了100.00%
内存: 击败了66.09%
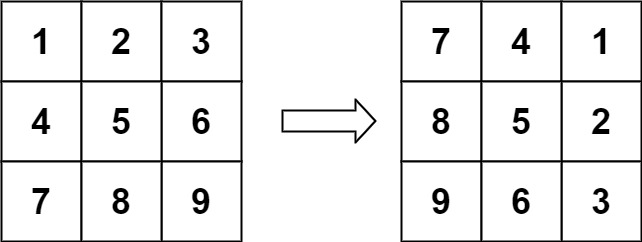
48.旋转图像
题意:
给定一个 n × n 的二维矩阵
matrix表示一个图像。请你将图像顺时针旋转 90 度。你必须在 原地 旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。
【输入样例】
matrix=[[1,2,3],[4,5,6],[7,8,9]
【输出样例】
[[7,4,1],[8,5,2],[9,6,3]
解题思路:
1. 找规律,第一行的第j个元素翻转后在倒数第一列的第j个元素;第二行的第j个元素翻转后在倒数第二列的第j个元素;
2. 以i表示行号,j表示列号,规律是:(i,j)-->(j,n-1-i)
3. 就是进行替换,替换这里因为要原地翻转数组,想到了之前练习过的轮转数组。ok尝试一下。
4. 这边跟轮转数组的区别是,一个二维数组,轮转了4次之后就会形成一个环。
5.循环次数
每一轮置换,可以将4个元素放在指定位置,因此,n*n个元素一共需要n*n/4次置换。
那行跟列怎么知道是遍历多少次呢?
嘿嘿,被分成了4等分,意味着我们行遍历n/2次,列遍历n/2次就够了,考虑到n为单数时,中间会多出来一列,此时列要遍历(n+1)/2,即保证向上取整。
class Solution {
public void rotate(int[][] matrix) {
int temp;//存储临时元素
int n = matrix.length;
for(int i=0;i<n/2;++i){
for(int j= 0;j< (n+1)/2; ++j){
temp = matrix[i][j];
matrix[i][j] = matrix[n-1-j][i];
matrix[n-1-j][i] = matrix[n-1-i][n-1-j];
matrix[n-1-i][n-1-j] = matrix[j][n-1-i];
matrix[j][n-1-i] = temp;
}
}
}
}时间: 击败了100.00%
内存: 击败了31.83%
73.矩阵置零
题意:
给定一个
m x n的矩阵,如果一个元素为 0 ,则将其所在行和列的所有元素都设为 0 。请使用 原地 算法。
【输入样例】
matrix=[[1,1,1],[1,0,1],[1,1,1]]
【输出样例】[[1,0,1],[0,0,0],[1,0,1]]
解题思路:
拿到题目的时候就想到一个很简单粗暴的方法;
定义两个数组a[i]和b[j],分别用来判断第i行和第j列是否有为0的元素;
遍历元素,对数组a和b进行赋值
再遍历数组,修改元素
class Solution {
public void setZeroes(int[][] matrix) {
//两个数组a和b,用来判断那一些列有0,哪一些没有0
int[] a = new int[matrix.length];//行
int[] b = new int[matrix[0].length];//列
for(int i=0;i<matrix.length;++i){
for(int j=0;j<matrix[0].length;++j){
if(matrix[i][j] == 0){
a[i] = 1;//所有i行,j列的数据都要为0
b[j] = 1;
}
}
}
for(int i=0;i<matrix.length;++i){
if(a[i] == 1){
for(int j=0;j<matrix[0].length;++j){
matrix[i][j] =0;
}
}
}
for(int j=0;j<matrix[0].length;++j){
if(b[j] == 1){
for(int i=0;i<matrix.length;++i){
matrix[i][j] =0;
}
}
}
}
}时间: 击败了100.00%,我这双重循环还能100%,没有想到哈哈
内存: 击败了59.17%