一 问题描述
在每台有故障的自动取款机上都贴着一个标签,提示客户去最近的取款机上取款。已知 n 台自动取款机的二维位置列表,为每台自动取款机都找到一个距离最近的自动取款机。
二 输入和输出
1 输入
第 1 行包含测试用例数 T(T≤15),每个测试用例都以取款机的数量 n 开始(2≤n ≤10^5 )。接下来的 n 行,每行都包含一台取款机的坐标 x、y(0≤x , y≤10^9 )。在一个测试用例中没有两个点重合。
2 输出
对每个测试用例,都输出 n 行,第 i 行表示第 i 个取款机与最近取款机的平方距离。
三 输入和输出样例
1 输入样例
2
10
17 41
0 34
24 19
8 28
14 12
45 5
27 31
41 11
42 45
36 27
15
0 0
1 2
2 3
3 2
4 0
8 4
7 4
6 3
6 1
8 0
11 0
12 2
13 1
14 2
15 0
2 输入样例
200
100
149
100
149
52
97
52
360
97
5
2
2
2
5
1
1
2
4
5
5
2
2
2
5
四 分析和设计
1 分析
本问题中的数据为二维数据,采用 KD 树进行二分搜索即可。
(1)根据输入数据的二维坐标创建 KD 树。
(2)在 KD 树中查询每个点 p 的最近点,输出平方距离。
2 设计
(1)数据结构定义。
可以预先用 p[] 复制一份原始序列,然后在 KD 树中查询 p[i]。也可以增加数据域存储原始 id 的方式存储数据。
(2)创建 KD 树。按照轮转法创建 KD 树,每层选择的维度都为层次与 k 取余,即 idx=dep%k 。本问题坐标为二维,k=2,则第 0 层选择第 0 维,第 1 层选择第 1 维,第 2 层选择第 0 维,第 3 层选择第 1 维,以此轮转。每层都按照当前维度进行比较,将中位数作为划分点,继续创建左右子树。idx 为当前层选择的维度。
(3)查询给定点p 的最近点。
创建 KD 树的方法不同,搜索方式也略有不同。本问题采用非存储型 KD 树,不要求输出最近点,只需输出到最近点的平方距离,因此不需要创建序对,而是定义一个变量 ans,记录 p 到最近点的平方距离。查询时,从树根开始,首先计算树根 a[mid] 与 p 的距离 dist,若 dist<ans,则更新 ans=dist。若 p.x[dim]
< a[mid].x [dim],则首先在左子树中查询,若以 ans 为半径的圆与树根的另一区域相交,即 rd<ans,则需要在右子树中查询,否则首先在右子树中查询。若以 ans 为半径的圆与树根的另一区域相交,即 rd<ans,则需要在左子树中查询。
五 代码
package com.platform.modules.alg.alglib.hdu2966;
import java.util.Arrays;
public class Hdu2966 {
private int N = 100010;
private Long inf = Long.MAX_VALUE;
int idx, k = 2;
public String output = "";
Long ans;
Node a[] = new Node[N];
Node p[] = new Node[N];
public Hdu2966() {
for (int i = 0; i < a.length; i++) {
a[i] = new Node();
}
for (int i = 0; i < p.length; i++) {
p[i] = new Node();
}
}
public String cal(String input) {
String[] line = input.split("\n");
int T, n;
T = Integer.parseInt(line[0]);
int count = 1;
while (T-- > 0) {
n = Integer.parseInt(line[count++]);
for (int i = 0; i < n; i++) {
String[] num = line[count++].split(" ");
for (int j = 0; j < k; j++) {
p[i].x[j] = Integer.parseInt(num[j]);
}
a[i] = p[i];
}
build(0, n - 1, 0);
for (int i = 0; i < n; i++) {
ans = inf;
query(0, n - 1, 0, p[i]);
output += ans + "\n";
}
}
return output;
}
Long dis(Node p, Node q) {
Long ret = 0L;
for (int i = 0; i < k; i++)
ret += (p.x[i] - q.x[i]) * (p.x[i] - q.x[i]);
return ret > 0 ? ret : inf;
}
void build(int l, int r, int dep) {
if (l > r) return;
int mid = (l + r) >> 1;
idx = dep % k;
Arrays.sort(a, l, r + 1);
build(l, mid - 1, dep + 1);
build(mid + 1, r, dep + 1);
}
void query(int l, int r, int dep, Node p) {
if (l > r) return;
int mid = (l + r) >> 1, dim = dep % k;
Long dist = dis(a[mid], p);
if (dist < ans)
ans = dist;
Long rd = Long.valueOf(((p.x[dim] - a[mid].x[dim]) * (p.x[dim] - a[mid].x[dim])));
if (p.x[dim] < a[mid].x[dim]) {
query(l, mid - 1, dep + 1, p);
if (rd < ans)
query(mid + 1, r, dep + 1, p);
} else {
query(mid + 1, r, dep + 1, p);
if (rd < ans)
query(l, mid - 1, dep + 1, p);
}
}
class Node implements Comparable<Node> {
int x[] = new int[2];
public int compareTo(Node o) {
return x[idx] > o.x[idx] ? 1 : -1; // 升序
}
}
}六 测试
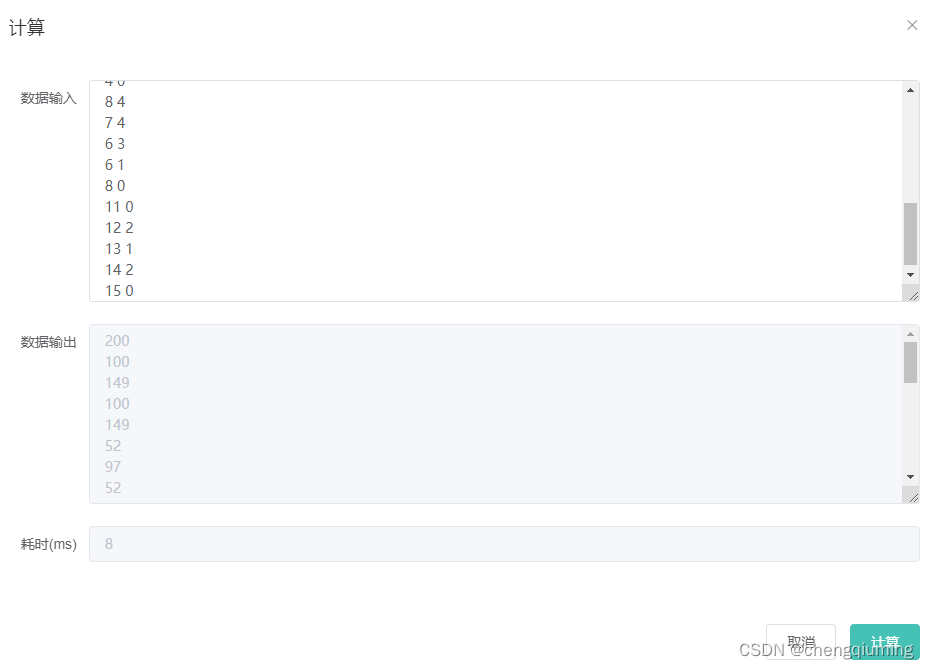


![[附源码]Node.js计算机毕业设计高校教材管理系统Express](https://img-blog.csdnimg.cn/54bd7bac56cb4a1da59ccbb402d5a635.png)



![[附源码]Python计算机毕业设计高校课程思政案例库系统Django(程序+LW)](https://img-blog.csdnimg.cn/9efa4a1350264aec9c6a832ae0b7dc6c.png)