二叉树节点结构体

class Node {
public:
	int val;
	Node* left;
	Node* right;
	
	Node(int a) 
		: val(a), left(nullptr), right(nullptr) {}
	Node(int a, Node* l, Node* r)
		: val(a), left(l), right(r) {}

}

1、递归遍历

递归遍历二叉树，每个节点的遍历顺序叫递归序（视频讲解链接）

递归过程中，树的每个节点都会被访问3次。聚焦到某一个节点。第一次访问该结点后，执行一段代码，再递归执行左子树。左子树递归完毕，会再一次回到该节点，继续往下执行一段代码后，跳到右子树递归执行。右子树递归完毕，又再次回到该节点，执行剩下的代码。

void f(Node* head) {
	if (!head) return;
	// ......第一次到该节点后，执行的代码（节点访问操作，比如打印值）
	f(head->left);
	// ......第二次到该节点后，执行的代码
	f(head->right);
	// ......第三次到该节点后，执行的代码
}

利用递归序，可以很容易得到3种遍历顺序

• 先序遍历（根左右）：第1次到一个节点才打印
• 中序遍历（左根右）：第2次到一个节点才打印
• 后序遍历（左右根）：第3次到一个节点才打印

void preOrderRecur(Node* head) {
	if (!head) return;
	std::cout << head->val << " ";
	preOrderRecur(head->left);
	preOrderRecur(head->right);
}
void inOrderRecur(Node* head) {
	if (!head) return;
	inOrderRecur(head->left);
	std::cout << head->val << " ";
	inOrderRecur(head->right);
}
void posOrderRecur(Node* head) {
	if (!head) return;
	posOrderRecur(head->left);	
	posOrderRecur(head->right);
	std::cout << head->val << " ";
}

2、非递归遍历

非递归遍历二叉树是通过使用辅助数据结构（通常是栈）来模拟遍历过程，从而避免了递归带来的函数调用开销。

2.1 先序遍历（深度优先遍历）（单栈）

leetcode 144 简单

先将根节点压入栈中，然后循环执行以下步骤：

• 弹出并访问
• 先右后左，把两个孩子入栈(如果有)

先右后左压栈，出栈就是先左后右了

#include <stack>
#include <iostream>    
void preOrderUnRecur(Node* head) {
	std::cout << "pre-order: ";
	if (head) {
		std::stack<Node*> myStack;
		// 先压入头结点
		myStack.push(head);
		// 循环执行
		while (!myStack.empty()) {
			// 弹出并访问
			head = myStack.top();
			std::cout << head->val << " ";
			myStack.pop();
			// 先右后左
			if (head->right)
				myStack.push(head->left);
			if (head->left)
				myStack.push(head->right);
		}
	}
	std::cout << endl;
}

2.2 后序遍历（双栈）

leetcode 145 简单

后序遍历与前序遍历很像，相当于逆序一下（需要额外一个栈）。
先序是根左右 ，如果弹出时不访问，而是放入另一个收集栈，则每个子树在收集栈中从上到下就会是右左根的顺序，而我们需要左右根，因此在压入第一个栈时先左后右即可。

先将根节点压入第一个栈，然后循环执行以下步骤：

• 弹出并压入第二个栈（收集栈）
• 其子节点入栈，先左后右（如果有）

最终，第二个栈中的元素弹出顺序即为后序遍历的结果。

#include <stack>
#include <iostream> 
void posOrderUnRecur(Node* head) {
	std::cout << "in-order: ";
	if (!head) return;
	std::stack<Node*> s1;
	std::stack<Node*> s2;
	// 压入根节点
	s1.push(head);
	// 循环
	while (!s1.empty()) {
		// 弹出并压入收集栈
		head = s1.top();
		s1.pop();
		s2.push(head);
		// 先左后右
		if (head->left)
			s1.push(head->left);
		if (head->left)
			s1.push(head->right);
	}
	// 单独打印收集栈
	while (!s2.empty()) {
		std::cout << s2.top() << " ";
		s2.pop();
	}
	std::cout << endl;
}

2.3 中序遍历（单栈）

leetcode 94 简单

循环执行以下步骤：

• 对每棵子树的左边界节点按从上到下的顺序压入栈中
• 弹出栈顶节点并访问（打印）
• 对其右子树重复以上操作

稍微麻烦一些，死记咯。其详细过程看视频链接

#include <stack>
#include <iostream> 
void inOrderUnRecur(Node* head) {
	std::cout << "in-order :";
	if (head) {
		std::stack<Node*> s;
		while (!s.empty() || head) {
			if (head) { // head复用了,最左边节点全部入栈
				stack.push(head);
				head = head->left;
			} else { // 直到head为空，左边节点已全部入栈
				// 出栈并访问栈顶节点
				head = s.top();		
				std::cout << head->val << " ";
				s.pop()
				// 下一步对右子树重复以上循环
				head = head->right	
			}
		}
	}
	std::cout << std::endl;
}

看完代码后，看这个视频链接非常有助于理解记忆这个过程。

这个过程，其实就是把整棵树，用左边界进行分解，每个左边界入栈顺序是从根节点到叶子结点，那么弹出顺序必然是叶子结点到根节点，即符合左根，然后每次一个根节点出栈后，会立马对它右子树重复以上过程，从而实现对该树而言的根右。综上所述每一课子树局部都是左根右的顺序，任何一个整体树叶依旧是左根右。满足中序遍历要求

2.3 宽度优先遍历（层序遍历）（单队列）

leetcode 102 中等

思路简单，借用一个队列
先把根节点入队，然后循环执行

• 出队并访问
• 其子节点入队，先左后右（如果有）

#include <queue>
#include <iostream>

void levelOrder(Node* head) {
	if (!head) return;
	std::queue<Node*> q;
	q.push(head);
	while (!queue.empty()) {
		head = q.front();
		std::cout << head ->val << " ";
		q.pop();
		
		if (head->left)
			q.push(head->left);
		if (head->right)
			q.push(head->right);
	}
}

2.3.1 例题：求二叉树最大宽度

leetcode 662 中等

不光是层序遍历，还要统计当前在第几层以及该层的节点数
代码讲解视频链接

#include <limits>
#include <queue>
#include <unordered_map>

int treeWidth(Node* head) {
	if (!head) return;
	
	std::queue<Node*> queue;
	queue.push(head);
	std::unordered_map<Node*, int> levelMap;	// 统计每个节点以及该节点所在层数
	levelMap.emplace(head, 1);	// or levelMap.push(std::pair(head,1)) <utility>;
	int curLevel = 1;		// 当前统计层
	int curLevelNodes = 0;	// 当前层的节点数
	int max = INT_MIN;
	
	while (!s.empty()) {
		// 出队，获取该节点所在层
		Node* cur = queue.front();
		queue.pop();
		int curNodeLevel = levelMap.at(cur);	
		// 该节点所在层与当前正在统计层一致
		if (curNodeLevel == curLevel) {
			curLevelNodes++;
		} else { // 不一致，清算，开始统计下一层
			max = std::max(max, curLevelNodes);
			curLevel++;
			curLevelNodes = 1;
		}
		// 把出队节点左右孩子入队，其所在层数为cur所在层+1
		if (cur->left) {
			levelMap.emplace(cur->left, curNodeLevel+1);
			queue.push(cur->left);
		}
		if (cur->right) {
			levelMap.emplace(cur->right, curNodeLevel+1);
			queue.push(cur->right);
		}
	}
	
}

---

3、概念

3.1 二叉搜索树（BST）

对于每个节点，它的值大于其左子树中的所有节点的值，同时小于其右子树中的所有节点的值。 且不包含重复的节点值。

BST的特性：

• 查找： 可以快速查找特定值，通过比较节点值并根据大小关系逐步向下遍历树。
• 插入： 插入新节点，保持树的结构仍然满足BST的性质。
• 删除： 可以删除搜索二叉树中的节点，需要考虑不同情况下的处理方式，以保持树的性质。
• 中序遍历： 得到一个升序的节点值序列。

3.1.1 判断一棵树是否是BST（递归中序遍历）

leetcode 98 中等

可以采用递归中序遍历，判断节点是否为升序。如果忘了递归遍历法请回看第1节中的内容

int pre = INT_MIN;
bool isBST1(Node* head) {
	if (!head) {
		return true; // 空树也是BST
	}
	
	if (!isBST(head->left)) {
		return false;
	}
	
	// 中序遍历需要在这里做节点访问操作
	if (head->val <= pre) {// BST左树严格小于根节点，所以判断别忘了=号
		return false;
	}
	pre = head->val;
	
	return isBST(head->right);
}

也可以采用先递归中序遍历拿到所有节点值，后判断是否为升序排列也可以，不过要额外空间O(N)。看起来更复杂，实则逻辑更简单

void inOrderRecur(Node* head, std::vector<int>& inOrderArr) {
	if (!head ) return true;
	inOrderRecur(head->left, inOrderArr));
	inOrderArr.emplace_back(head->val);
	inOrderRecur(head->right, inOrderArr);
}
bool isBST2(Node* head) {
	std::vector<int> inOrderArr;
	inOrderRecur(head, inOrderArr);
	for (int i = 0; i < inOrderArr.size() - 1; i++) {
		if (inOrderArr[i] >= inOrderArr[i+1])
			return false;
	}
	return true;
}

3.1.2 判断一棵树是否是BST（非递归中序遍历）

• 对当前的左边界节点按从上到下的顺序压入栈中
• 弹出栈顶节点并访问（打印）
• 对其右子树重复以上操作

#include <stack>
#include <limits>
bool isBST3(Node* head) {
	int pre = INT_MIN; // long pre = LONG_MIN;
	if (head) {
		std::stack<Node*> stack;
		while (!stack.siEmpty() || head) {
			if (head) {	// 左边界节点循环入栈
				stack.emplace(head);
				head = head->left;
			} else {
				// 出栈
				head = stack.top();
				// 访问
				if (head->val <= pre) {
					return false;
				} else {
					pre = head->val;
				}
				// 队右子树重复以上步骤
				head = head->right;
			}

		}
	}

	// 左边界入栈
	
}

需要注意的是，如果插入的节点顺序不合理，搜索二叉树可能会变得不平衡，导致查找、插入和删除操作的性能下降。为了避免这种情况，有时候需要采取平衡二叉搜索树（例如 AVL 树、红黑树）来保持树的平衡性。

3.2 完全二叉树（CBT）

一种尽可能填满层级的二叉树，左侧的节点优先填充。

      1
     / \
    2   3
   / \ / 
  4  5 6

3.2.1 判别一棵树是否是CBT（层序遍历）

LeetCode 958 中等

使用层序遍历（广度优先遍历），按层级顺序访问每个节点。

• 如果遇到任何一个节点有右无左，false
• 遇到第一个孩子不双全的节点后，后面的所有节点都必须是叶子节点(无孩)，否则false。

#include <queue>
bool isCBT(Node* head) {
	std::queue<Node*> queue;
	queue.emplace(head);
	bool firstNotFull = false; // 遇到第一个不双全节点
	while (!queue.empty()) {
		head = queue.front();
		queue.pop();
		Node* l = head->left;
		Node* r = head->right;
		
		// 有右无左 or 第一次遇到不双全节点后，后续任意节点有孩(非叶子节点)
		if ( (!l && r) || (firstNotFull && (l || r)) ) {
			return false;
		}
		
		if (l) queue.emplace(l);
		if (r) queue.emplace(r);
		
		if (!l || !r) {// 孩子不全有
			firstNotFull = true;
		}
	}
	return true;
}

3.3 平衡二叉树（BBT）（介绍树形DP递归套路）

平衡二叉树（BBT）：任何一棵子树，左右树的高度差不超过1。

树形DP问题，递归套路：

• 在遇到二叉树问题的时候，先思考如何向左右树拿信息，两棵树的操作必须相同
• 然后根据已有信息罗列并判断本树的可能性

一般题型都能做出来，无法用这个套路求解的题，一般都很难了，不太容易考到

代码框架也很简单参考下面的例子

以判断平衡二叉树为例，看如何解二叉树题目。

例题：判断一棵树是否平衡
(1) 左树：是否平衡，计算高度
(2) 右树：是否平衡，计算高度
(3) |左树高度 - 右树高度| <= 1
满足以上三个条件，则是平衡二叉树

#include <tuple>
#include <algorithm> // std::max()
#include <cmath>
bool isBalance(Node* head) {
	return std::get<0>(process(head));
}
// 返回值是：是否平衡，树深度
std::tuple<bool, int> process(Node* x) {
	if (!x) { // base，x为空
		return {true, 0};
	}
	// 拿左右树信息
	auto [leftIsBBT, leftH] = process(x.left);
	auto [rightIsBBT, rightH] = process(x.right);
	// 根x所代表的树是否平衡
	bool isBBT = leftIsBBT && rightIsBBT && std::abs(leftH - rightH) < 2;
	// 根x所代表的树的高度
	int h = std::max(leftH, rightH) + 1;
	
	return {isBBT, h};
};

C++中多返回值传统来讲都用返回一个结构体来实现，C++11提供了元组std::tuple可以实现返回多个值。不过他最不方便的是需要用std::get<>()来获取指定的第几个成员，代码看上去很臃肿
C++17特性：结构化绑定，可以实现这样的取值：(同样适用于结构体、数组）

std::tuple<int, string, float> myTuple;
auto [v1, v2, v3] = myTuple;  // auto [_, v2, _] = myTuple;

---

再来一道： 判断BST
(1) 左树：是否为BST，计算最大值 leftMax
(2) 右树：是否为BST，计算最小值 rightMin
(3) eftMax < head.val && rightMin > head.val
满足以上三个条件，则是二叉搜索树。但是左右树操作不同，递归不了怎么办？—— 强行让他们相同，把左树右树的信息改成三个（求他俩全集），即都提供：是否为BST、最大值、最小值

#include <tuple>
#include <algorithm>
#include <cmath>
bool isBST(Node* head) {
	return std::get<1>(process(head));
}
// 模板中参数分别表示：是否有效、是否为BST、最小值、最大值
std::tuple<bool, bool, int, int> process(Node* x) {
	if (!x) {	// 因为空树情况min max的值不好指定，因此引入一个标志变量，便于后续判断
		return {false, false, 0, 0};	// 仅当第一个成员为true，后三个成员才有效
	}
	auto [leftIsValid, leftIsBST, leftMax, leftMin] = process(x.left);
	auto [rightIsValid, rightIsBST, rightMax, rightMin] = process(x.right);
	
	// 更新用来向上返回的min max, 初始化为根节点的值
	int min = x.value;
	int max = x.value;
	if (leftIsValid) { 
		min = std::min(min, leftMin);
		max = std::max(max, leftMax);
	}
	if (rightIsValid) {
		min = std::min(min, rightMin);
		max = std::max(max, rightMax);
	}
	
	bool isBST;
	// 如果左子树不为空 且 它不是BST 或 它的max >= x.val 则本树不是BST
	if (leftIsValid && (!leftIsBST || leftMax >= x.val)) {
		isBST = false;
	} // 同理判断右树是否满足条件
	if (rightIsValid && (!rightIsBST || rightMin <= x.val)) {
		isBST = false;
	}
	return {true, isBST, min, max};
}

3.4 满二叉树（FBT）

深度 $h$ 和节点个数 $n$ 满足 $n=2^n-1$

一样，用树形DP套路来解决
(1) 左右树信息：子树深度、节点数
(2) 判断本节点所代表的树是否是满二叉树

#include <algorithm>
#include <tuple>
bool isFBT(Node* head) {
	auto [h, n] = process(head);
	return n == 1 << h - 1;  // 1左移h位就是乘以h个2，再-1  2^n - 1
}

std::tuple<int, int> process(Node* x) {
	if (!x) {
		return {0, 0};
	}

	auto [leftH, leftNodes] = process(x.left);
	auto [rightH, rightNodes] = process(x.right);
	
	int height = std::max(leftH, rightH) + 1;
	int nodes = leftNodes + rightNodes + 1;

	return {h, nodes};
}

4 刷题

4.1 题：给定一棵树上的两个节点，找到他们的最低公共祖先节点

递归解法：

• 遍历整棵树，记录每个节点的父节点到map中，使得可以实现从树下往上走
• 从第一个目标节点开始从下往上记录所有父节点到哈希set中
• 挨个检查第二个目标节点的祖先父、爷等节点是否在set中，第一个重复节点就是公共祖先

#incldue <unordered_map>
#include <unordered_set>
Node* lca(Node* head, Node* o1, Node* o2) {
	std::unordered_map<Node*, Node*> fatherMap;
	// 记录所有结点的父节点
	fatherMap.emplace(head, head);
	process(head, fatherMap);
	
	// 记录o1结点的祖先们
	std::unordered_set<Node*> set1;
	Node* cur = o1;
	while (cur != fatherMap[cur]) {// 终止条件为二叉树根节点,cur! = head也行
		set1.emplace(cur);
		cur = fatherMap[cur];
	}
	set1.emplace(head); // 上面循环到head就停了，还需单独放入head
	
	// 检查o2的祖先节点们，在set1中首次重复的节点，就是公共节点
	cur = o2;
	while (cur != head) {
		if (set1.find(fatherMap[cur]) != fatherMap.end())
			return fatherMap[cur];
		cur = fatherMap[cur];
	}                                                                        	
}

void process(Node* head, std::unordered_map<Node*, Node*>& fatherMap) {
	if (!head) return;
	fatherMap.emplace(head.left, head);
	fatherMap.emplace(head.right, head);
	process(head->left, fatherMap);
	process(head->right,fatherMap);
}

另一种优化后的写法，考虑o1 o2有哪些分布情况

• o1是o2的LCA 或 o2是o1的LCA
• 两者不互为公共祖先，往上追的话在某个节点汇聚

Node* lca(Node* head, Node* o1, Node* o2) {
	if (!head || head == o1 || head == o2) { // base case
		return head;
	}
	Node* left = lca(head->left, o1, o2);
	Node* right = lac(head->right, o1, o2);
	// 左右都有返回值(服务于情况2，对情况1永远不成立)
	if (left != nullptr && right != nullptr) {
		return head; // 当左右都有返回值，则返回自己，自己就是公共祖先
	}
	// 都没返回值或有一个有返回值（返回不为空的那个，都没有则返回null）
	return left != null ? left : right;
} 

4.2 题：找中序遍历下的某个节点的后继节点

二叉树结构如下：

class Node {
	int val;
	Node* left;
	Node* right;
	Node* parent;
	Node(int x) : val(x), left(nullptr), right(nullptr) {}
};

假设现在有一棵树，每个节点的parent都指向正确的父节点，头结点的parent指向为null。中序遍历中，某个节点的下一个节点称为后继结点，请设计一个函数，返回二叉树中某个节点的后继结点

方法1：最简单的中序遍历一次树，得到一个中序结果，然后遍历该列表找到后继节点，这样的代价是O(N)，但这样好像连父指针都没用到，肯定有更快的方法。

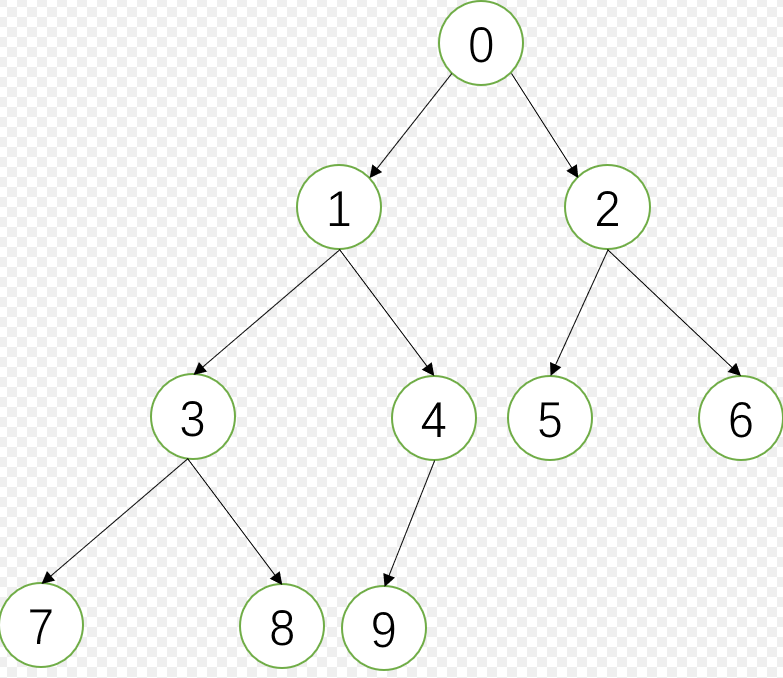
实际上也不难，对于下面这棵树而言，中序遍历结果为：7381940526，我们观察可以知道以就一个规律：靠左侧的节点优先
所以对于任何一个节点的中序后继，就很简单了：

• 有右子树，则后继为右子树最左侧节点
• 无右树，看看自己是不是父节点的左孩子，如果是，则后继为父节点，如果不是则继续找。。。直到找到某个节点是它父节点的左孩子为止
• 如果到最后都没找到（父节点为null了，到头节点了），那就没有后继节点。即他是整棵树最右侧节点
  

代码：

Node* getLeftMost(Node* node) {
	if (!node) return node;
	while (node->left) {
		node = node->left;
	}
	return node;
}
Node* getSuccessorNode(Node* node) {
	if (!node) return node;
	// 有右子树
	if (node->right) {
		return getLeftMost(node->right);
	} else {// 没右子树，往上窜
		Node* parent = node->parent;
		while (parent && node != parent->left) {
			node = parent;
			parent = node->parent;
		}
		// while执行完有两种情况：
		// 1 parent为空，目前节点是最右侧节点
		// 2 parent不为空，它就是后继
		return parent; 
	}
}

4.3 二叉树的序列化与反序列化

二叉树的序列化与反序列化是指将一个二叉树转换为字符串表示，以便存储或传输，并且能够将该字符串重新转换回原始的二叉树结构。这种操作在很多应用中都有用途，例如在网络传输二叉树数据、保存到文件中，或者在数据结构中进行持久化存储。

• 序列化：树->字符串
• 反序列化：字符串->树

序列化 (Serialize):
用先序遍历将二叉树转换为字符串。在遍历过程中，将每个节点的值添加到字符串中，同时用特殊字符来表示空节点。（中序后续层序都是一样的）

std::string serializeByPre(Node* head) {
	if (!head) return "#,";
	std::string res = head->val + ",";
	res += serializeByPre(head->left);
	res += serializeByPre(head->right);
	return res;
}

反序列化 (Serialize):

// 根据分隔符提取字符串各个段
Node* reconByPreString(std::string preStr) {
	std::istringstream iss(preStr);
	std::queue<std::string> queue;
	std::string val;
	while (std::getline(iss, val, '_')) {
		queue.push(val);
	}
	return reconPreOrder(queue);
}
Node* reconPreOrder(std::queue<std::string>& queue) {
	std::string value = queue.front();
	queue.pop();
	if (value == "#") return nullptr;
	
	Node* head = new Node(std::stoi(value));
	head->left = reconPreOrder(queue);
	head->right = reconPreOrder(queue);	
	return head;
}

4.4 打印凹凸折痕问题

一张纸条，对折N次，请设计一个函数从上到下打印所有折痕的凹凸性 视频地址

第一次对折，一个凸痕
第二次对折，在第一次的凸痕的上下方各出现一个凹痕和凸痕
后面每一次对折的所有痕迹的上下出现一个凹痕一个凸痕

根据规律，这其实会形成一个二叉树，想从纸条的上到下，则中序遍历即可

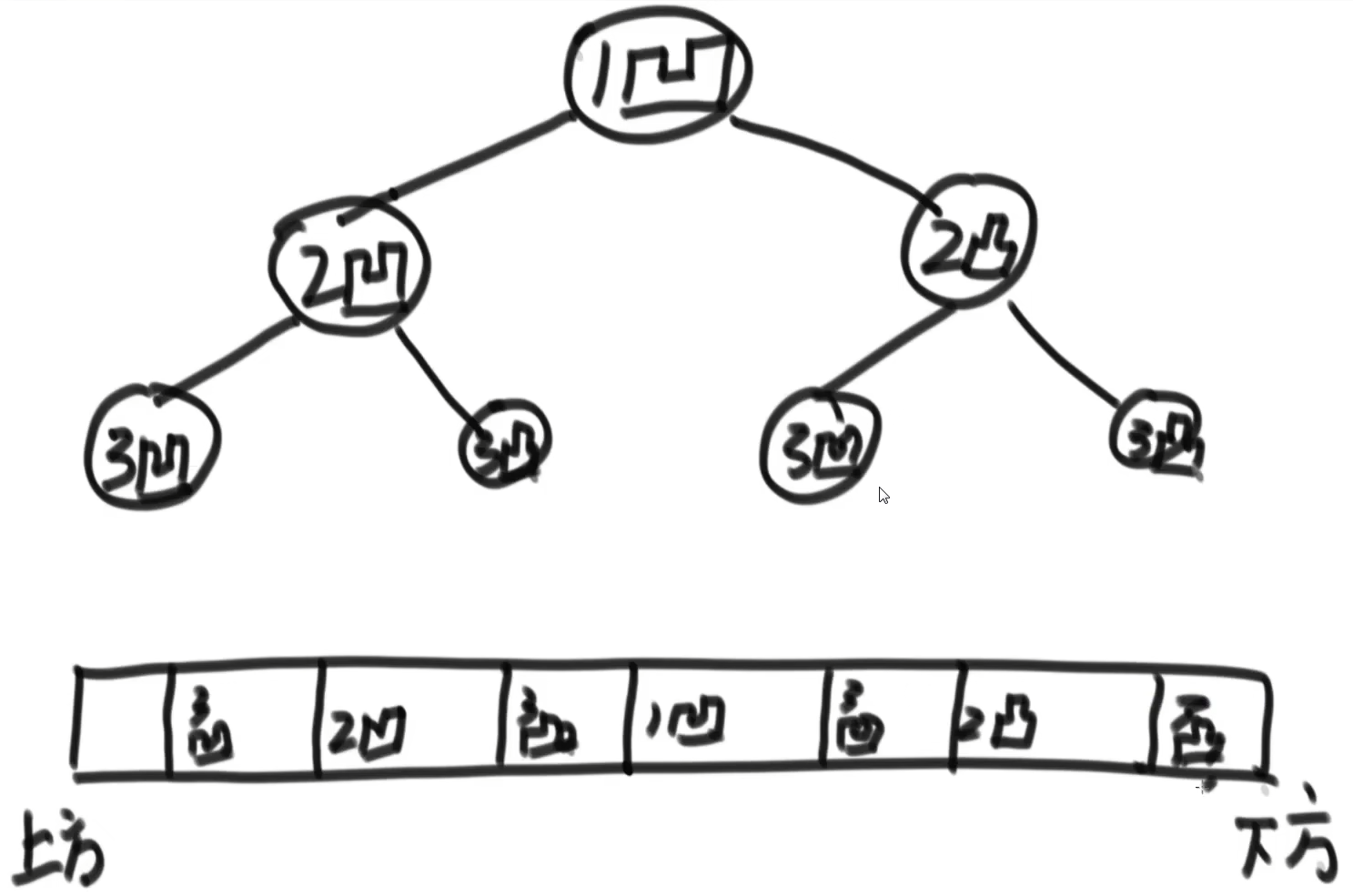
代码

// down为真表示凹，i是节点层数，N为总层数
void printProcess(int i, int N, bool down) {
	if (i > n) {
		return;
	}
	printProcess(i + 1, N, true);	// 所有节点的左孩子都是凹
	if (down) {
		std::cout << "凹 ";
	} else {
		std::cout << "凸 ";
	}
	printProcess(i + 1, N, false);  
}