论文导读｜European Journal of Operational Research近期文章精选：旅行商问题专题

推文作者：王松阁

编者按

在“European Journal of Operational Research近期论文精选”中，我们有主题、有针对性地选择了European Journal of Operational Research中一些有趣的文章，不仅对文章的内容进行了概括与点评，而且也对文章的结构进行了梳理，旨在激发广大读者的阅读兴趣与探索热情。在本期“论文精选”中，我们以“旅行商问题”为主题，分别探究了先行约束广义旅行商问题、广义近似旅行商问题、非对称旅行商问题，涉及整数规划、分支切割、锥规划、迭代贪心等诸多知识。

推荐文章1

● 题目：Precedence constrained generalized traveling salesman problem: Polyhedral study, formulations, and branch-and-cut algorithm

先行约束广义旅行商问题：多面体研究、公式化和分支切割算法

● 期刊：European Journal of Operational Research

● 原文链接：https://doi.org/10.1016/j.ejor.2023.01.039

● 作者：Daniil Khachai, Ruslan Sadykov, Olga Battaiaa, Michael Khachay

● 关键词：

Travelling salesman(旅行商问题),Integer programming(整数规划),Branch-and-cut algorithm(分支切割算法),Facet-inducing inequalities(面诱导不等式),Polyhedral structure(多面体结构)

● 摘要：

The Precedence Constrained Generalized Traveling Salesman Problem (PCGTSP) is an extension of two well-known combinatorial optimization problems - the Generalized Traveling Salesman Problem (GTSP) and the Precedence Constrained Asymmetric Traveling Salesman Problem (PCATSP), whose path version is known as the Sequential Ordering Problem (SOP). Similarly to the classic GTSP, the goal of the PCGTSP, for a given input digraph and partition of its node set into clusters, is to find a minimum cost cyclic route (tour) visiting each cluster in a single node. In addition, as in the PCATSP, feasible tours are restricted to visit the clusters with respect to the given partial order. Unlike the GTSP and SOP, to the best of our knowledge, the PCGTSP still remain to be weakly studied both in terms of polyhedral theory and algo-rithms. In this paper, for the first time for the PCGTSP, we propose several families of valid inequalities, establish dimension of the PCGTS polytope and prove sufficient conditions ensuring that the extended Balas' pi- and sigma-inequalities become facet-inducing. Relying on these theoretical results and evolving the state-of-the-art algorithmic approaches for the PCATSP and SOP, we introduce a family of MILP-models (formulations) and several variants of the branch-and-cut algorithm for the PCGTSP. We prove their high performance in a competitive numerical evaluation against the public benchmark library PCGTSPLIB, a known adaptation of the classic SOPLIB to the problem in question.

先行约束广义旅行商问题（PCGTSP）是两个著名的组合优化问题的扩展，分别是广义旅行商问题（GTSP）和先行约束不对称旅行商问题（PCATSP），其路径版本被称为顺序排列问题（SOP）。与经典GTSP类似，对于给定的输入有向图和将其节点集划分为簇的方式，PCGTSP的目标是找到一个最小成本的环路（路径），使得每个簇都在一个节点中被访问。此外，与PCATSP类似，可行的路径被限制为按照给定的偏序访问簇。与GTSP和SOP不同的是，就我们所知，PCGTSP在多面体理论和算法方面仍然缺乏深入研究。在本文中，我们首次针对PCGTSP提出了几类有效的不等式，建立了PCGTSP多面体的维度，并证明了确保扩展的Balas' π - 和 σ -不等式成为面诱导的充分条件。基于这些理论结果，并借鉴了PCATSP和SOP的最先进算法方法，我们提出了一系列线性整数规划（MILP）模型和PCGTSP的分支定界算法的多个变体。我们证明了它们在公共基准库PCGTSPLIB上进行的竞争性数值评估中表现出很高的性能，该基准库是将经典SOPLIB改编成与问题相应的版本。

● 文章结构：

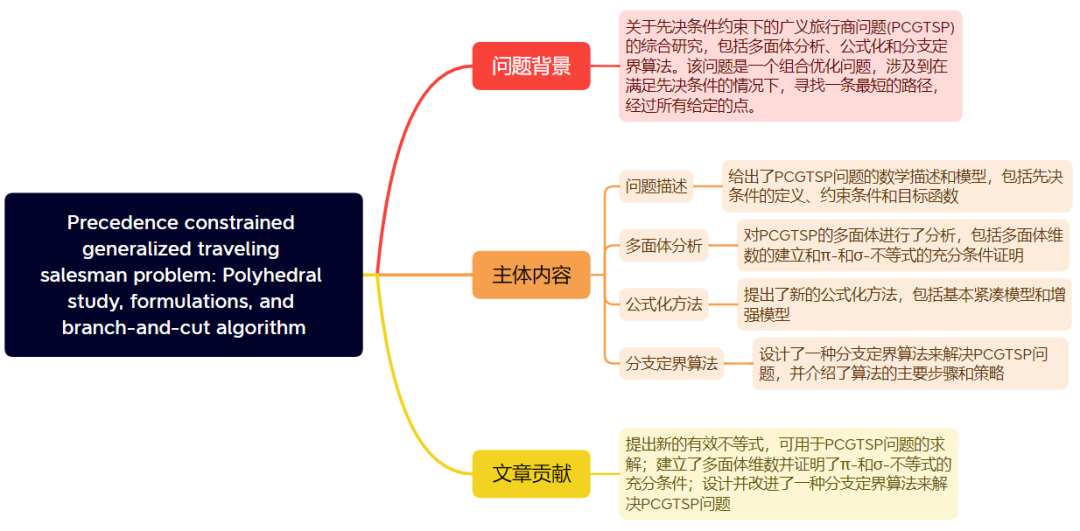
● 点评：

本文对先行约束广义旅行商问题 (PCGTSP)进行了系统研究，涵盖了多面体研究和算法分析两个方面。文章扩展了已有的PCATSP结果，提出了多种新颖的有效不等式，并对PCGTS多面体的维度进行了分析。也首次为PCGTSP问题提出了一种分支切割算法，为解决该问题提供了新的算法思路。

推荐文章2

● 题目：The generalized close enough traveling salesman problem

广义近似旅行商问题

● 期刊：European Journal of Operational Research

● 原文链接：https://doi.org/10.1016/j.ejor.2023.04.010

● 作者：Andrea Di Placido, Claudia Archetti, Carmine Cerrone, Bruce Goldend

● 关键词：

Metaheuristics(元启发式算法)，Close enough traveling salesman problem(广义近似旅行商问题)，Genetic algorithms(遗传算法)，Conic programming(锥规划)

● 摘要：

This paper studies a generalization of the close enough traveling salesman problem referred to as the generalized close enough traveling salesman problem (GCETSP). The canonical problem contains a set of customers, each associated with an area (neighborhood) that is generally circular. In the GCETSP, each customer is associated with a set of disks with different radii. Having multiple disks around the customer allows us to model several real-world applications, in which a higher benefit is gained by more closely approaching each target. A prize is assigned to each disk and is collected if the disk is traversed. The goal is to determine the route that visits each customer and the depot and maximizes the difference between the total collected prize and the route length. The total collected prize is given by the sum of the customer prices' associated with the innermost disk traversed by the route. We propose a heuristic algorithm and an evolutionary approach, specifically, a genetic algorithm (GA), to solve this problem. We evaluate the GA's performance on instances generated from benchmark CETSP and TSP instances. We then compare GA solutions with CETSP solutions and solutions obtained through an alternative approach based on pre-selecting intersection points with customers' disks. The results show that the GA can identify high-quality solutions with a short computing time.

本文研究了近似旅行商问题的一种推广，称为广义近似旅行商问题（GCETSP）。经典问题包含一组客户，每个客户与一个圆形的区域相关联。在GCETSP中，每个客户与一组具有不同半径的圆盘相关联。围绕一位客户有多个不同圆盘来模拟现实世界的几种不同应用，更接近目标的圆盘会获得更高效益。每个圆盘具有对应的奖励值，穿越该圆盘时即可获得相应奖励。目标是确定访问每个客户和中转站的路线，最大化总收集奖励和路线长度的差值，总收集奖励为路线穿越的最内圆盘所对应的客户价格之和。我们提出了一种启发式算法和一种遗传算法（GA）来解决这个问题，并利用CETSP和TSP的基准算例所生成的实例来评估遗传算法的性能。然后将GA的解与CETSP解以及通过基于预先选择与客户圆盘的交点的替代方法所得到的解进行比较，结果显示GA能够在短时间内识别出高质量的解。

● 文章结构：

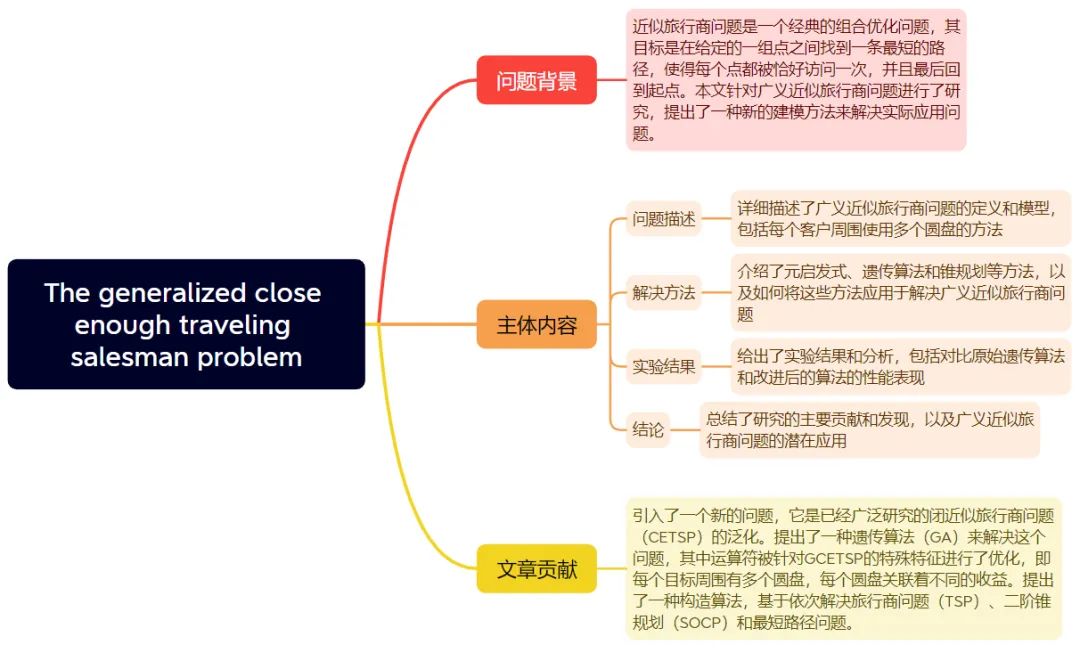
● 点评：

本文采用遗传算法（GA）和构造算法来解决GCETSP问题。GA针对GCETSP的特殊特点进行了优化，构造算法则基于解决TSP、SOCP和最短路径问题的顺序来构建可行路径。这两种方法为解决GCETSP提供了有效的工具。通过与另一种启发式方法nearOpt进行对比实验，GA表现出更好的性能。本研究在无人机使用中的抄表、RFID系统等现实应用的建模优化中具有一定启示。

推荐文章3

● 题目：An asymmetric traveling salesman problem based matheuristic algorithm for flowshop group scheduling problem

一种基于非对称旅行商问题的数学启发式算法，用于流水车间群调度问题

● 期刊：European Journal of Operational Research

● 原文链接：https://doi.org/10.1016/j.ejor.2023.03.038

● 作者：Xuan He, Quan-Ke Pan, Liang Gao, Janis S. Neufeld

● 关键词：

Scheduling(调度)，Asymmetric traveling salesman(非对称旅行商)，Branch-and-cut(分枝切割法)，Iterated greedy(迭代贪心)，Matheuristic(数学启发式)

● 摘要：

The flowshop group scheduling problem (FGSP) has become a hot research problem owing to its practical applications in modern industry in recent years. The FGSP can be regarded as a combination of two cou-pled sub-problems. One is the group scheduling sub-problem with sequence-dependent setup times. The other is the job scheduling sub-problem within each group. A mixed integer linear programming model is built for the FGSP with the makespan criterion. Based on the problem-specific knowledge, i.e., the sequence-dependent group setup times are greater than the processing time of jobs, and the number of machines is small, the group scheduling sub-problem is approximated into an asymmetric traveling sales-man problem (ATSP). Then, a matheuristic algorithm (MA) is proposed by integrating a branch-and-cut algorithm and an iterated greedy (IG) algorithm, where the branch-and-cut algorithm is used to generate the optimal Hamiltonian circuit for sub-group sequences of a group sequence obtained by the IG. On 405 test instances, the proposed MA performs significantly better than several state-of-the-art algorithms in the literature.

近年来，由于在现代工业中的实际应用，流水车间群调度问题（FGSP）已成为一个热门的研究问题。FGSP可以看作是两个耦合子问题的组合。一个是带有序列相关设置时间的群调度子问题，另一个是每个群内的作业调度子问题。针对以最大完工时间为目标的FGSP，建立了一个混合整数线性规划模型。基于问题特定的知识，即序列相关的群设置时间大于作业的处理时间，并且机器数量较少，将群调度子问题近似为不对称旅行商问题（ATSP）。然后，提出了一种数学启发式算法（MA），它将分支定界算法和迭代贪心（IG）算法结合在一起，其中分支定界算法用于为由IG得到的群序列的子群序列生成最优哈密顿回路。在405个测试实例上，所提出的MA表现明显优于文献中几种最先进的算法。

● 文章结构：

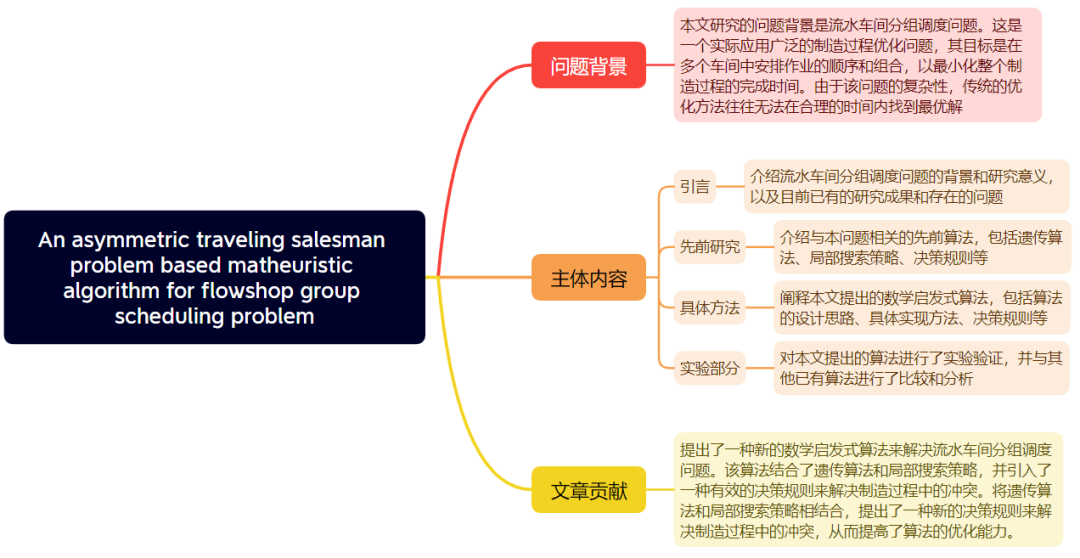
● 点评：

本研究主要针对流水车间分组调度问题（FCSP）的最大完工时间准则展开研究，提出了一种新颖的数学启发式算法（MA）。研究创新点包括在问题层面上将分组调度子问题近似为非对称旅行商问题（ATSP），并在算法层面上采用分支定界和迭代贪心算法的结合。还针对问题特点设计了特殊的局部搜索和断续规则机制，以增强迭代贪心算法的搜索性能。该算法在解决能够近似为非对称旅行商问题的流水车间调度问题上表现出色，对于一些经典的流水车间调度问题，如无等待流水车间调度问题和阻塞流水车间调度问题，该算法同样适用。