确实，面积应该是没有正负的，或者说和曲面的定向应该是无关的。我们用微分形式的积分定义了具有参数形式的曲面的面积。所以这个意思就是说，对于不同的曲面的定向，微分形式应该也不同。 

 

这就是体形式的具体样子，得到每个向量的组成的矩阵的行列式。根据标架确定正负号。

体形式的定义让我们明白了，对于任何一个标架，你的微分k形式是相容的。或者说取了一个k形式，对应的标架是相容的。这样让面积总是为正的。

这里指出，要确定k维曲面的面积，需要嵌入到更高维的空间进行计算。 

 

这个做法非常有意思，对于n-1维曲面，体形式既可以看成n-1维曲面的面积，也可以看成n维曲面的体积，只要保证高为1就行。等式(7)后面有大用处。

 可以看到，我们把等式7继续推导，可以得到等式8，然后，取任何一个正交基向量作为新的高，可以得到等式(9).而V(x)(ei,.....)这个行列式展开就可以得到（10），ei的坐标应该是(0,0,...1,...0,0)

所以，我们得到了这么几个重要的等式。首先对于面积微元ds等于法向量的每个分量和对应的两个二形式的乘积的和。这里要注意，ds只是一个符号，是一个体形式。同样根据公式（10）可以得到后面的结果。

 

 

上面就是第一类积分。其中定向S改变，对应的体形式的符号也会一起改变。 

这里第二类曲面积分就是直接把体形式和系数放到一起变成一个普通的微分形式。

接下来是几个重要的公式：

 

 

 

 

 

 

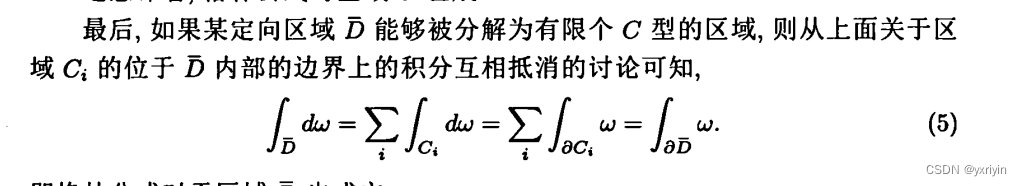
这里我跳过了大部分证明。相比起证明，我觉得更重要的还是理解这个一般的斯托克斯公式。然后再倒推前面的几个特殊情形。一般的斯托克斯公式说的是，对于一个k维曲面，它上面的k-1形式w，对于dw在曲面上的积分，等于在他的边界上的w的积分。这个物理含义我们在后面的章节继续学习。

 

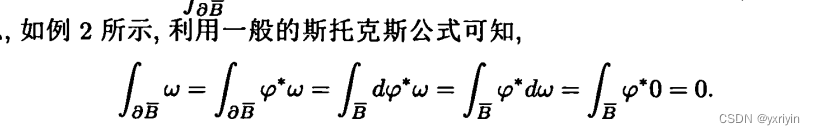
这里还有一个知识点，就是拉回映射和微分算子d是可交换的，这个在流形里面会学习。

然后我们看斯托克斯公式在三维下的各种情况。首先是二维中，二维中的平面，它的边界是一条线，所以可以推出格林公式：

 

 注意，二维里面的1形式只有Pdx+Qdy这种。

考虑三维，有两种情况，首先是三维里面的三维物体，它的边界是二维曲面。按照上面的思路，应该有：

注意，三维下的二维曲面只有Pdy^dz +Qdz^dx+Rdx^dy这种形式。

最后就是三维下的二维曲面，它的边界是一维曲线。

 

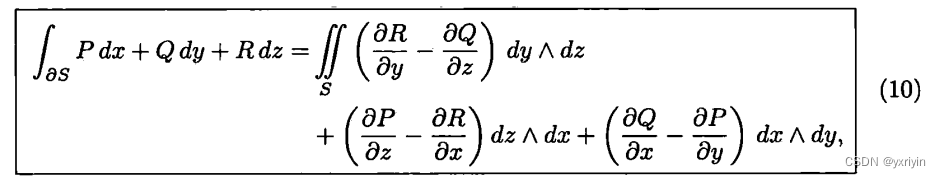
不在赘述了。终于结束这个章节了，后面还有几章，不得不说卓里奇的书真的是醍醐灌顶。