HoudiniVex笔记_P25_ForceExtended力进阶

news2024/11/14 4:00:01

原视频：https://www.youtube.com/playlist?list=PLzRzqTjuGIDhiXsP0hN3qBxAZ6lkVfGDI
Bili：Houdini最强VEX算法教程 - VEX for Algorithmic Design_哔哩哔哩_bilibili

Houdini版本：19.5

如有错误，可在评论区指正。

1、本章主要讲引力相关

万有引力公式：

本章主要是根据引力相关进行延伸、拓展等，（l 为距离，direction为运动的方向），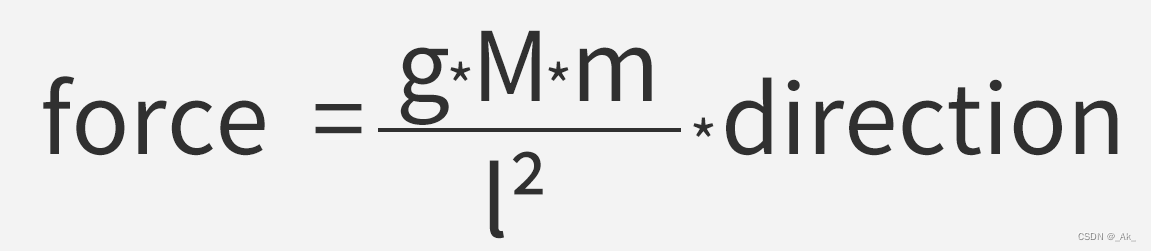

还有个关于万有引力的相关重要知识点： 引力的大小跟这两个物体的质量的乘积成正比，跟它们的距离的二次方成反比。

 2、引力

本小节来实现下引力，总体难度不大，原理如下图，

 eg.①先上结果，主要是根据上面，

②节点连接及设置，更多的是对参数进行设置、调试，

③补充，解算器solver内的attractor_force节点代码如下，

float massM = f@mass;
float massA = point(1, 'mass', 0);

vector attractorPos = point(1, 'P', 0);

float l = distance(@P, attractorPos);

float g = point(1, 'gravitation', 0);

vector v = normalize(attractorPos - @P);    //运动方向

float s = massM * massA * g / (l * l);
s= clamp(s, chf('minforce'), chf('maxforce'));    //谨防出现无穷大或无穷小的力

vector force = v * s;

v@vel += force;
v@vel = normalize(v@vel) * min(length(v@vel), chf('maxspeed')); //对速度进行限制

v@P += v@vel;

 3、多重引力

多个引力体与多个被吸引体。

eg.①先上结果，案例与上面差不多，

②节点连接及设置，可对参数进行设置、调试，看看不同参数的结果，

③补充，解算器solver内的attractor_force节点代码如下，

float massM = f@mass;

//该点受到不同引力体吸引的的总引力
vector totalForce = set(0,0,0);
for(int i=0; i<npoints(1); i++){
    float massA = point(1, 'mass', i);
    
    vector attractorPos = point(1, 'P', i);
    
    float l = distance(@P, attractorPos);
    
    float g = point(1, 'gravitation', i);
    
    vector v = normalize(attractorPos - @P);    //运动方向
    
    float s = massM * massA * g / (l * l);
    s= clamp(s, chf('minforce'), chf('maxforce'));  //谨防出现无穷大或无穷小的力
    
    vector force = v * s;
    totalForce += force;
}

v@vel += totalForce;
v@vel = normalize(v@vel) * min(length(v@vel), chf('maxspeed')); //对速度进行限制

v@P += v@vel;

 4、引力与朝向

与前面相同，这次设置了法线(@N= 速度)，以及使引力体动起来。

eg.①先上结果，

②节点连接及设置，
③ 补充，两个解算器内的代码如下， attractor_force节点

//solver5节点内的代码：引力体对象在范围内随机运动
vector pos = @P * 0.01;
vector4 pos4 = set(pos.x, pos.y, pos.z, @Time);

vector f1 = curlnoise(pos4);
vector f2 = set(0,0,0);

//在体积外层，给一个往内的力，把它拉回来
float val = volumesample(1, 'surface', @P);
if(val>0){
    f2 = -volumegradient(1, 'surface', @P);
}

vector force = (f1 + f2) * chf('k');

v@vel += force;
v@vel= normalize(v@vel) * min(length(v@vel), chf('maxvel'));

@P += v@vel;
//    solver4内的attractor_force节点代码
float massM = f@mass;

//该点受到不同引力体吸引的的总引力
vector totalForce = set(0,0,0);
for(int i=0; i<npoints(1); i++){
    float massA = point(1, 'mass', i);
    
    vector attractorPos = point(1, 'P', i);
    
    float l = distance(@P, attractorPos);
    
    float g = point(1, 'gravitation', i);
    
    vector v = normalize(attractorPos - @P);    //运动方向
    
    float s = massM * massA * g / (l * l);
    s= clamp(s, chf('minforce'), chf('maxforce'));    //谨防出现无穷大或无穷小的力
    
    vector force = v * s;
    totalForce += force;
}

v@vel += totalForce;
v@vel = normalize(v@vel) * min(length(v@vel), chf('maxspeed')); //对速度进行限制

v@P += v@vel;

v@N = normalize(v@vel);

5、角向力/旋转力

以力作角度，绕引力体做环绕运动。原理大概如下，

 eg.①老规矩，先上结果，
② 节点连接及设置，

③补充，解算器solver内的angular_force节点代码如下， 

vector posC = point(1, 'P', 0);
float massC = point(1, 'mass', 0);
float massM = f@mass;
float g = point(1, 'gravitation', 0);
float l = distance(@P, posC);

float f = massM * massC * g / (l * l);
f = min(f, chf('maxforce'));

f@ang += f;
f@ang = min(f@ang, chf('maxang'));

matrix mat = ident();
rotate(mat, f@ang, set(0,1,0));

@P -= posC; //要旋转，先归位至轴点。否则默认以(0,0,0)为轴点旋转
@P *= mat;
@P += posC;

6、自转与角运动 

与【5的例子】类似，对被吸引的对象添加自转运动，
关于自转，只关注自身，其它的力(如引力)不管，原理大概如下，

 eg.①结果略
② 直接使用【5、角向力/旋转力】的案例，仅对修改部分进行标注，节点连接及设置如下，

③补充，解算器solver内的angular_motion节点代码如下， 

float mass = f@mass;
float g = f@gravitation;  //一个自定义力，或者说是系数

float force = mass * g;
force = min(force, chf('maxforce'));

f@angM += force;
f@angM = min(f@angM, chf('maxang'));

matrix mat = ident();
rotate(mat, f@angM, set(0,1,0));

v@N *= mat;

7、单摆运动

原理大概如下，

 eg.在Houdini中实现单摆运动，
①节点连接及设置如下，

②补充，完整代码如下， 

f@ang = radians(chf('ang'));    // 角度随意

vector axis = set(0,0,1);
matrix mat = ident();
rotate(mat, f@ang, axis);

@P *= mat;
f@mass = chf('mass');       // 角度随意
f@pscale = f@mass * 0.2;    // 尺寸随意
float l = prim(0, 'perimeter', 0);
float g = chf('gravity');     //设为0.5/任意值
float mass = f@mass;

float force = -g * mass * sin(f@ang) / l;
f@vel += force;
f@vel *= chf('damping');  //衰减系数（摩擦力之类），设为0.995/任意值

f@ang += f@vel;

vector dir = set(0, -1, 0);
matrix mat = ident();
rotate(mat, f@ang, set(0,0,1));
dir *= mat;

@P = dir * l;

 ③结果略

8、多对象单摆运动

与【7、单摆运动】差不多，这次使用For-each-number循环生成多条单摆线，

 eg.①节点连接及设置如下，

 ②完整代码如下，

//  解算器Solver内代码节点的代码

//ball属性的点，代码执行
int prim = pointprims(0, @ptnum)[0];    //该点所在的primitive
int pivotpt = primpoints(0, prim)[0];   //该primitive的第一个点作为轴点

vector pivotPos = point(0, 'P', pivotpt);   //轴点位置

float l = prim(0, 'perimeter', prim);
float g = chf('gravity');     //设为0.5/任意值
float mass = f@mass;

float force = -g * mass * sin(f@ang) / l;
f@vel += force;
f@vel *= chf('damping');  //衰减系数（摩擦力之类），设为0.995/任意值

f@ang += f@vel;

vector dir = set(0, -1, 0);
matrix mat = ident();
rotate(mat, f@ang, set(0,0,1));
dir *= mat;

@P = pivotPos + dir * l;
//    setup节点内代码，循环生成多条线
int ite = detail(1, 'iteration');
int numite = detail(1, 'numiterations');

@P.z = ite; 

float minlen = chf('minlen');
float maxlen = chf('maxlen');

float y = fit(ite, 0, numite-1, 0, $PI * 4);
y = -fit11(sin(y), minlen, maxlen);

if(inpointgroup(0, 'ball', @ptnum) == 1){ //保险起见，加多ball做判断条件
    @P.y = y;
}

 9、弹力

 具有约束性的弹力，就像单摆加了根弹力绳，

受力分析及公式推导大概如下 ，

eg.①在Houdini里实现上面动图的效果，节点连接及设置如下，

②补充，完整代码如下，

//  init6 节点代码

f@mass = chf('amss');     //参数设为1或随意
f@targetlength = chf('target'); //参数设为0.5或随意

f@pscale = f@mass * 0.25;
v@vel = set(0,0,0);
//解算器内的spring_force节点代码

vector pivotPos = point(0, 'P', 0);
vector v = normalize(pivotPos - @P);

float l = distance(pivotPos, @P);
float tl = f@targetlength;
float diffl = l - tl;
float n = chf('stiffness'); //  "绳子"的弹性系数

vector f1 = v * f@mass * (diffl * diffl) * diffl / abs(diffl) * n ;
f1 = normalize(f1) * min(length(f1), chf('maxforce1'));

vector f2 = set(0, -1, 0) * chf('gravity') * f@mass;

v@vel += f1;
v@vel += f2;

v@vel *= chf('dampling');   //摩擦系数

@P += v@vel;

③可以去试试调下参数，感受各个参数对结果的影响。

10、弹力“链”

这次是实现下面这种效果，

受力分析及公式推导大概如下 ，

 eg.①在Houdini里实现上面动图的效果，节点连接及设置如下，

②补充，完整代码如下，

//    init7 节点代码，节点类型为Points

if(@ptnum == 0 || @ptnum == npoints(0) - 1){
    //后面用作固定首末两个点
    setpointgroup(0, 'pin', @ptnum, 1);
}

f@mass = chf('mass');   //设为0.1或随意
v@vel = set(0,0,0);
//    init_prim 节点代码，类型为Primitives
f@targetlength = f@perimeter;
//    spring_force节点代码，节点类型为Primitives

int pts[] = primpoints(0, @primnum);

//每两个点之间的弹力
for(int i=0; i<len(pts); i++){
    int pt1 = pts[i];
    int pt2 = pts[(i+1) % len(pts)];
    
    vector pos1 = point(0, 'P', pt1);
    vector pos2 = point(0, 'P', pt2);
    float mass1 = point(0, 'mass', pt1);
    float mass2 = point(0, 'mass', pt2);
    
    vector v = normalize(pos2 - pos1);
    float l = distance(pos1, pos2);
    float tl = f@targetlength;
    float diffl = l - tl;
    
    float n = chf('stiffness');
    
    vector force = v * (diffl * diffl) * (diffl / abs(diffl)) * n;//  *mass1 * mass2 *    
    force = normalize(force) * min(length(force), chf('maxforce'));
    
    setpointattrib(0, 'vel', pt1, force, 'add'); 
}
//    gravity_force 节点代码，类型为Points

vector force = set(0, -1, 0) * chf('gravity');

v@vel += force * f@mass;
//    update_pos 节点代码，节点类型为Points

if(inpointgroup(0, 'pin', @ptnum) == 0){
    //非首末两个点，位置更新
    v@vel *= chf('dampling');   //摩擦系数
    @P += v@vel;
}else if(@ptnum == 0){  //第一个点，位置更新
    @P = point(1, 'P', 0);
}

没有又找不着翻译，不能倍速看，很烦，只能啃英语生番原速看…

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/908429.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

sql数据导出到excel

sql数据导出到excel

一、打开Navicat Premium 12 二、导出
阅读更多...
管理类联考——逻辑——真题篇——按知识分类——汇总篇——三、综合推理——是否确定信息

管理类联考——逻辑——真题篇——按知识分类——汇总篇——三、综合推理——是否确定信息

真题&#xff08;2018-40&#xff09;——综合推理——是否确定信息——确定信息——以确定信息作为解题起点 某海军部队有甲、乙、丙、丁、戊、己、庚7艘舰艇&#xff0c;拟组成两个编队出航&#xff0c;第一编队编列3艘舰艇&#xff0c;第二编队编列4艘舰艇&#xff0c;编列…
阅读更多...
linux的http服务

linux的http服务

Web通信基本概念 基于B/S&#xff08;Browser/Server&#xff09;架构的网页服务 服务端提供网页 浏览器下载并显示网页 Hyper Text Markup Lanuage,超文本标记语言 Hyper Text Transfer Protocol&#xff0c;超文本传输协议 虚拟机A&#xff1a;构建基本的Web服务 [root…
阅读更多...
python Requests

python Requests

Requests概述 官方文档&#xff1a;http://cn.python-requests.org/zh_CN/latest/,Requests是python的HTTP的库&#xff0c;我们可以安全的使用 Requests安装 pip install Requests -i https://pypi.tuna.tsinghua.edu.cn/simple Requests的使用 Respose的属性 属性说明url响…
阅读更多...
Jeep车型数据源：提供Jeep品牌车系、车型、价格、配置等信息

Jeep车型数据源：提供Jeep品牌车系、车型、价格、配置等信息

​​​​​ Jeep是一个极具特色的汽车品牌&#xff0c;它的所有车型都注重实用性&#xff0c;具有越野性能和高性能。Jeep品牌在汽车行业中的口碑一直是非常不错的。如果你想要了解Jeep品牌车系、车型、价格、配置等信息&#xff0c;就可以通过挖数据平台Jeep车型数据源API接口…
阅读更多...
IO day 5

IO day 5

1、使用两个线程完成两个文件的拷贝&#xff0c;主线程拷贝前一半内容&#xff0c;子线程拷贝后一半内容&#xff0c;并且主线程要阻塞回收子线程资源 #include <myhead.h>//定义求文件长度函数 int fd1,fd2; //以只读的形式打开源文件 if((fd1open(stcfile,O_RDONLY)) …
阅读更多...
aosp-刷入Magisk面具获取root权限

aosp-刷入Magisk面具获取root权限

作者&#xff1a;上山打鼠 一、简介 话说上次root手机都已经是初中的时候了&#xff0c;那时候捣鼓手机不亦乐乎&#xff0c;Android4.4的系统先解锁&#xff0c;再刷入第三方Recovery&#xff0c;然后再刷入Root包去获取Root权限 想学点逆向的知识&#xff0c;所以要root一下…
阅读更多...
算法通关村第5关【青铜】| Hash和队列的特征

算法通关村第5关【青铜】| Hash和队列的特征

1.Hash基础 &#xff08;1&#xff09;基础 哈希也称为散列&#xff0c;通过算法变成固定长度的输出值&#xff0c;存入对应的位置 例如这个算法为取模算法&#xff0c;indexnumber 模 7 存入1到15 &#xff08;2&#xff09;碰撞处理 当多个元素映射到同一位置上时就产生…
阅读更多...
L Grayscale Confusion【2023牛客多校第10场】【拓扑排序】

L Grayscale Confusion【2023牛客多校第10场】【拓扑排序】

来源&#xff1a;“范式杯”2023牛客暑期多校训练营10 —— L Grayscale Confusion 题意&#xff1a;给定 n 个三元组 ( r i , g i , b i ) 。构造一个长度为 n 的数组 w&#xff0c; 使得 ①w1 w 2 ②对于任意 i, j &#xff0c;若 r i > r j , g i > g …
阅读更多...
python之Numpy

python之Numpy

ndarray数组对象 NumPy定义了一个n维数组对象&#xff0c;简称ndarray对象&#xff0c;它是一个一系列相同类型元素组成的数组集合。数组中的每个元素都占有大小相同的内存块 ndarray 对象采用了数组的索引机制&#xff0c;将数组中的每个元素映射到内存块上&#xff0c;并且按…
阅读更多...
C++笔记之虚函数重写规则、返回类型协变、函数的隐藏

C++笔记之虚函数重写规则、返回类型协变、函数的隐藏

C笔记之虚函数重写规则、返回类型协变、函数的隐藏 code review! 文章目录 C笔记之虚函数重写规则、返回类型协变、函数的隐藏1.返回类型协变2.C中函数的隐藏 —— C Primer Plus &#xff08;第6版&#xff09; —— cppreference 1.返回类型协变 2.C中函数的隐藏 在C中&a…
阅读更多...
深入理解AQS和ReentrantLock

深入理解AQS和ReentrantLock

AQS 之前介绍synchronized关键字时提到过管程的概念&#xff0c;synchronized就是JVM内置管程&#xff0c;其使用的是管程的MESA模型。但是synchronized有一些缺点&#xff1a; 非公平锁&#xff0c;可能会使得一些线程长久抢占不到锁&#xff0c;导致其处于饥饿状态&#xf…
阅读更多...
5.分布式事务管理-Seata

5.分布式事务管理-Seata

由于Transactional注解只能控制所在服务器A的事务&#xff0c;当方法中调用其他服务器B的方法&#xff0c;当A中该方法出错时&#xff0c;Transactional只能回滚A中该方法中的SQL&#xff0c;而A调用B的方法中的SQL无法回滚 1.Seata Seata&#xff08;分布式事务解决方案&…
阅读更多...
Electron入门，项目运行，只需四步轻松搞定。

Electron入门，项目运行，只需四步轻松搞定。

electron 简单介绍&#xff1a; 实现&#xff1a;HTML/CSS/JS桌面程序&#xff0c;搭建跨平台桌面应用。 electron 官方文档&#xff1a; [https://electronjs.org/docs] 本文是基于以下2篇文章且自行实践过的&#xff0c;可行性真实有效。 文章1&#xff1a; https://www.cnbl…
阅读更多...
Centos开启防火墙和端口命令

Centos开启防火墙和端口命令

Centos开启防火墙和端口命令 1. 开启查看关闭firewalld服务状态2. 查看端口是否开放3. 新增开放端口4. 查看开放的端口 1. 开启查看关闭firewalld服务状态 #启动/关闭firewall systemctl start/stop firewalld #查看防火墙状态 systemctl status firewalld #禁用或者启用 syst…
阅读更多...
sql in mac学习记录

sql in mac学习记录

鉴于有一段时间没有访问mysql了&#xff0c;最近打算在mac 系统上下载mysql 练习一下sql的使用&#xff0c;于是 First, the mysql download https://dev.mysql.com/downloads/mysql/ Second, Mysql install steps Install the software by normally install one software …
阅读更多...
mysql 、sql server trigger 触发器

mysql 、sql server trigger 触发器

sql server mySQL create trigger 触发器名称 { before | after } [ insert | update | delete ] on 表名 for each row 触发器执行的语句块## 表名&#xff1a; 表示触发器监控的对象 ## before | after : 表示触发的时间&#xff0c;before : 表示在事件之前触发&am…
阅读更多...
cloud_mall-notes02

cloud_mall-notes02

1、多条件分页查询page ApiOperation("多条件分页查询xxxx")GetMapping("page")PreAuthorize("hasAuthority(模块权限:权限:page)")public ResponseEntity<Page<实体类>> loadxxxxPage(Page<实体类> page,实体类 domain) {pag…
阅读更多...
磁盘满了解决办法

磁盘满了解决办法

磁盘满了解决办法 1.添加硬盘2.查看是否添加成功3.创建分区4.查看卷名5.扩容6.7.8. 1.添加硬盘 2.查看是否添加成功 lsblk注&#xff1a;若没有&#xff0c;需要partprobe刷新或者重启 3.创建分区 fdisk /dev/sdb4.查看卷名 vgdisplay5.扩容 vgextend centos /dev/sdb16. …
阅读更多...
Docker安装MySQL、Redis如何自启？

Docker安装MySQL、Redis如何自启？

1、问题&#xff1a; Docker自启&#xff1a;http://t.csdn.cn/L2v55 重新启动虚拟机&#xff0c;Docker自动启动之后&#xff0c;发现MySQL、Redis都没有启动。 docker ps 没查到有启动的容器。 docker ps -a 查看所有的容器。 2、先使用 su root 命令&#xff0c;切换到root…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023