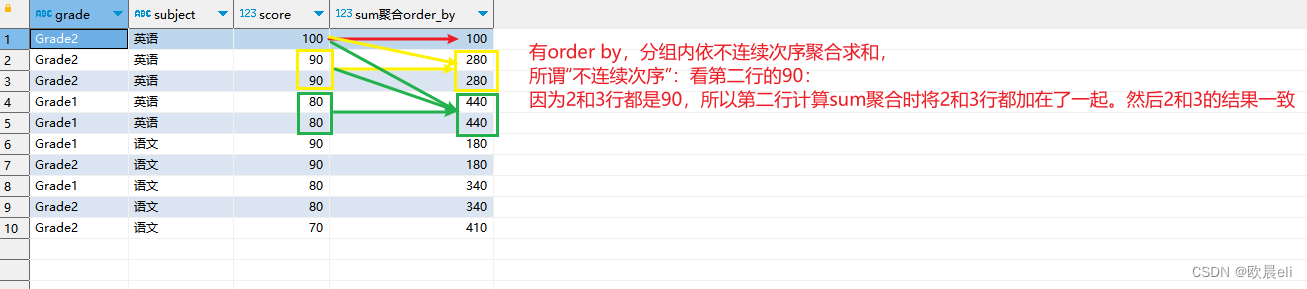
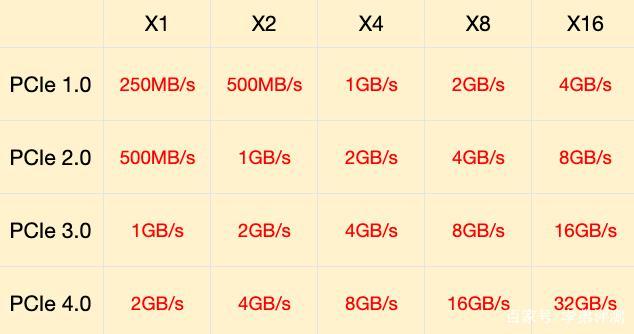
又一个奇技淫巧。
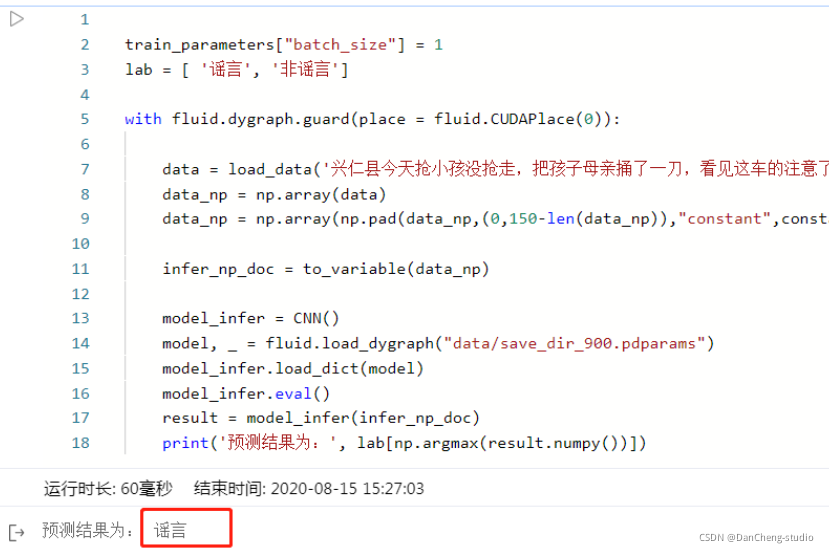
【例1】
∫ 0 1 d y ∫ y 1 x 3 + 1 d x = ? \int _0 ^1 dy \int _{\sqrt y} ^ 1 \sqrt{x^3 + 1} dx = ? ∫01dy∫y1x3+1dx=?
解析:
不说话,看下图:
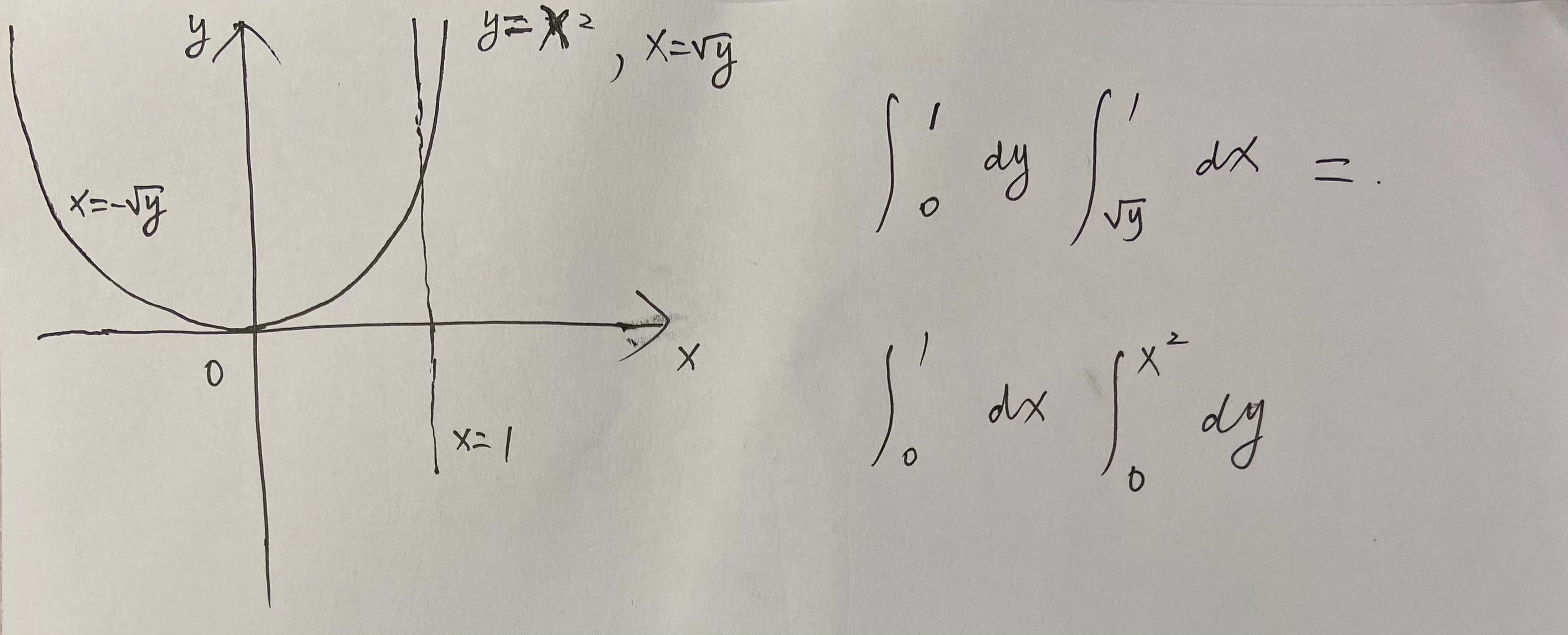
∫ 0 1 d y ∫ y 1 x 3 + 1 d x = ∫ 0 1 d x ∫ 0 x 2 x 3 + 1 d y = ∫ 0 1 x 2 x 3 + 1 d x = 1 3 ∫ 0 1 x 3 + 1 d ( x 3 + 1 ) = 1 3 ∫ 0 1 2 3 d ( x 3 + 1 ) 3 2 = 2 9 ( x 3 + 1 ) 3 2 ∣ 0 1 = 2 9 ( 2 2 − 1 ) \int _0 ^1 dy \int _{\sqrt y} ^ 1 \sqrt{x^3 + 1} dx =\\ \int _0 ^1 dx \int _{0} ^{x^2} \sqrt{x^3 + 1} dy =\\ \int _0 ^1 x^2 \sqrt{x^3 + 1} dx = \\ \frac{1}{3} \int_0 ^1 \sqrt{x^3 + 1} d(x^3+1) = \\ \frac{1}{3} \int_0 ^1 \frac{2}{3} d(x^3+1)^{\frac{3}{2}} = \\ \frac{2}{9}(x^3+1)^{\frac{3}{2}} | _0 ^ 1 = \\ \frac{2}{9} (2\sqrt {2} - 1) ∫01dy∫y1x3+1dx=∫01dx∫0x2x3+1dy=∫01x2x3+1dx=31∫01x3+1d(x3+1)=31∫0132d(x3+1)23=92(x3+1)23∣01=92(22−1)
【例2】
f ( x ) = ∫ 0 x c o s t 2 t − 3 π d t ,求 f ( x ) 在 [ 0 , 3 π 2 ] 上的平均值 f ˉ ( x ) f(x) = \int _0^x \frac{cos t}{2t - 3\pi}dt , 求f(x)在[0,\frac{3\pi}{2}]上的平均值\bar f(x) f(x)=∫0x2t−3πcostdt,求f(x)在[0,23π]上的平均值fˉ(x)
答案截图:
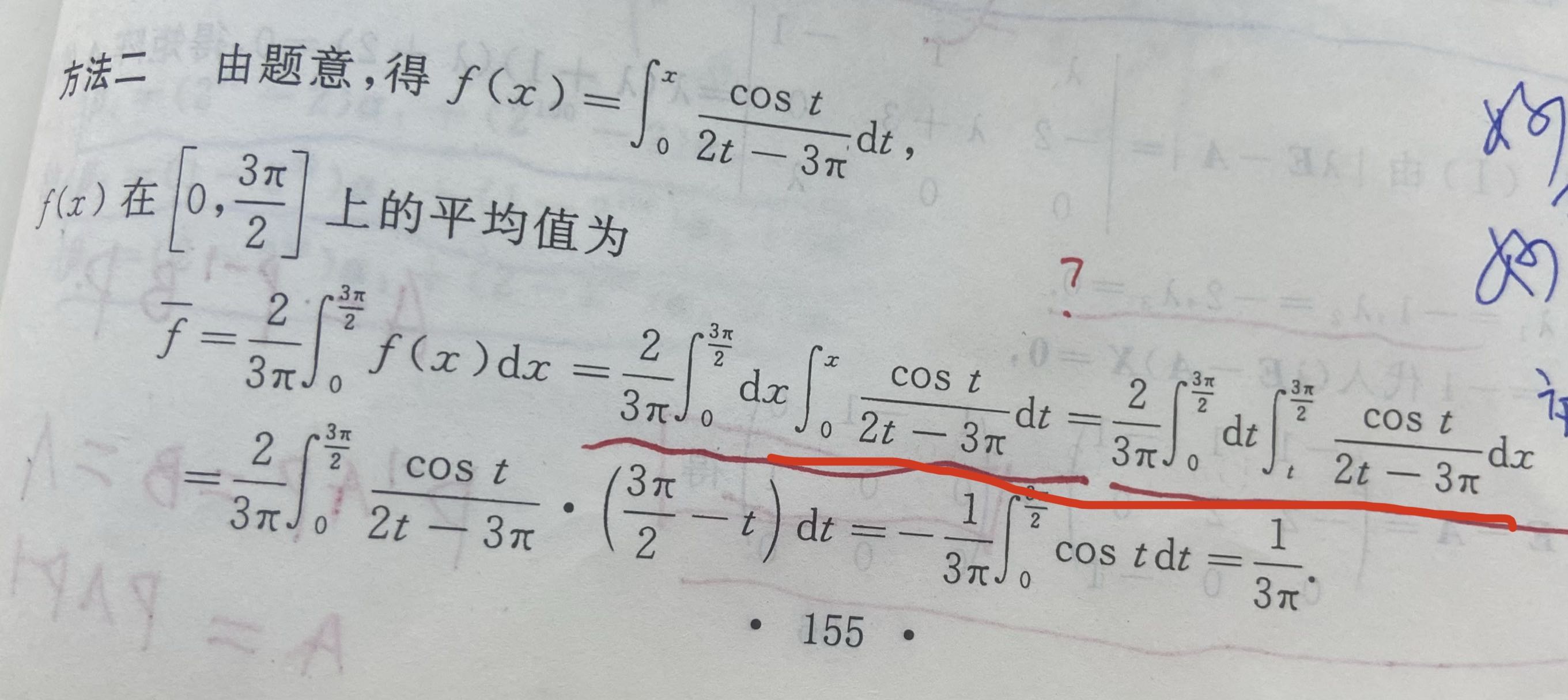
思路:题目是关于t和x的二重积分,t和x我们用的少,不太容易理解它们的转化。我们将t代换为x,x代换为y,这样看起来就比较熟悉了。

由上图可见,原式可化为:
2 3 π ∫ 0 3 π 2 c o s t 2 t − 3 π d x ∫ x 3 π 2 d t = − 1 2 2 3 π ∫ 0 3 π 2 c o s t d x = 1 / 3 π \frac{2}{3\pi}\int _0 ^{\frac{3 \pi}{2} } \frac{cos t}{2t - 3\pi } dx \int _x ^{\frac{3 \pi}{2}} dt = \\ -\frac{1}{2} \frac{2}{3\pi} \int _0 ^{\frac{3 \pi}{2} } cos tdx = 1/3\pi 3π2∫023π2t−3πcostdx∫x23πdt=−213π2∫023πcostdx=1/3π
总结:
- 二重积分交换积分次序要结合图形,这样比较简单方便,凭空想象是比较困难的。
- 二重积分如果两个未知数之间不是独立的,而是有一定的函数关系,此时,直接交换积分式时要小心。而假如两个未知数之间是独立的,那么两个积分可以任意组合,相当于两个单次积分之积。