前言

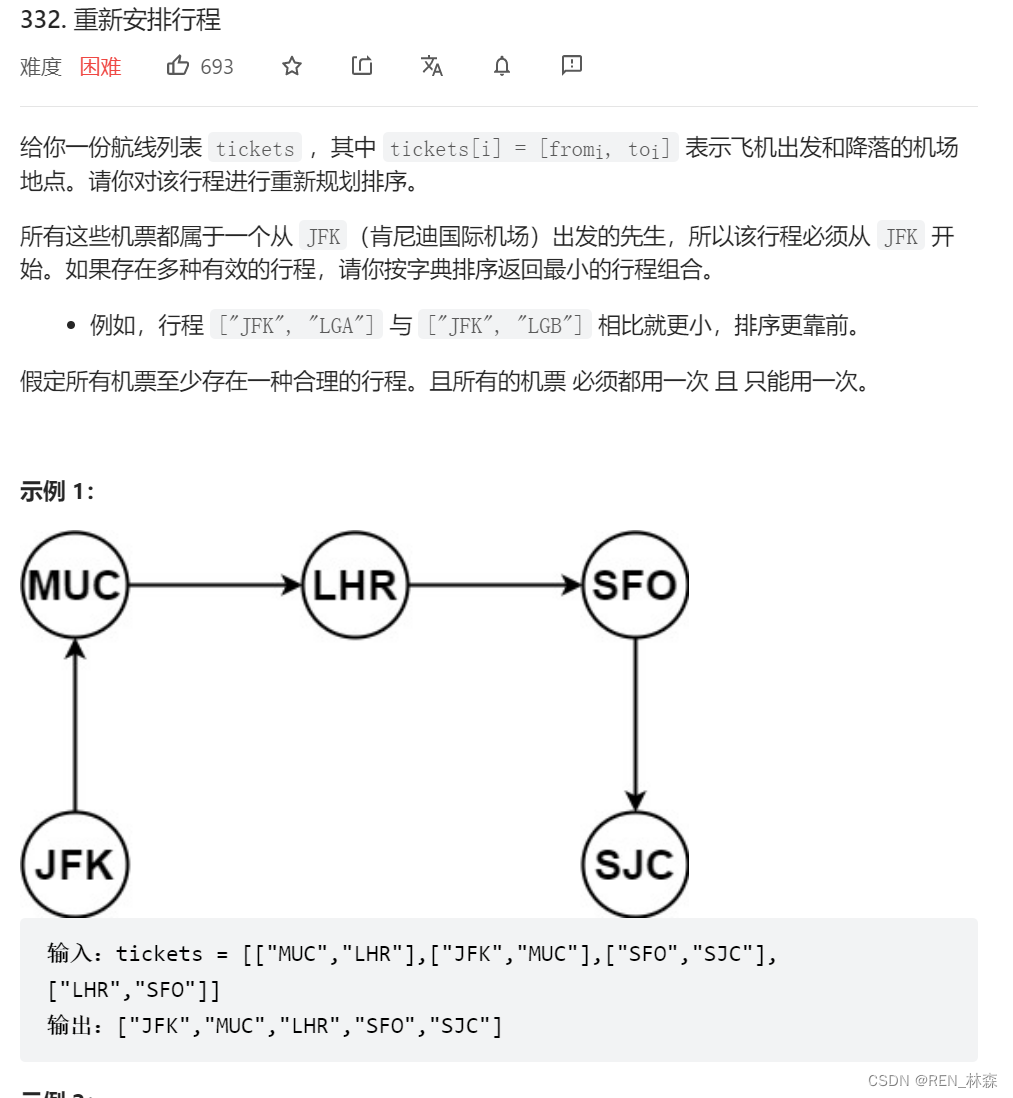
欧拉路径 == 从图的一个节点出发，每条边只访问一次，遍历完了所有图节点，这条路径为欧拉路径。

一、案例

在这里插入图片描述

二、回溯

按照上面的例子，很容易理解欧拉路径。
但是有一个很关键的点就是，可能多条路径，走到了那条死胡同路径，就是提前到达了终点，示例如下，
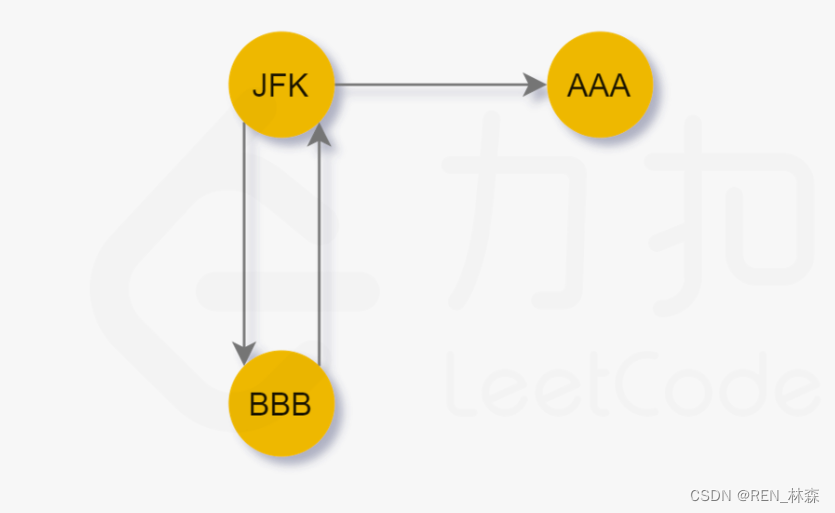
在这里插入图片描述
JFK -> AAA，就先走到了死胡同！！！关键点就在于解决死胡同问题。

一条欧拉路径，易知死胡同就是终点，那么遇到死胡同将其压栈到栈底作为终点，删除该死胡同节点，继续DFS遇到下一个死胡同就是倒数第二个节点，依次类推，一个个死胡同就压入栈中，而出栈顺序就是欧拉路径。

三、源码

class Solution {
    // 欧拉path问题。
    // 一定存在一条合理欧拉path，那么遇到一个死胡同就是末尾节点，删点这个死胡同，再遇到的死胡同就是倒数第二个节点，依次类推。
    // 需要最小字典序欧拉path，所以边需要末节点的字典序排序，采用优先队列。
    final static String next = "JFK";
    public List<String> findItinerary(List<List<String>> tickets) {
        // 建图
        buildGraph(tickets);
        // 以JFK为起点DFS
        dfs(next);
        // 出栈得到欧拉path，并返回。
        return getPath();
    }
    public List<String> getPath(){
        List<String> rs = new ArrayList<>();
        while(!postions.isEmpty()){
            rs.add(postions.pop());
        }
        return rs;
    }
    // DFS
    Stack<String> postions = new Stack<>();
    public void dfs(String pos){
        PriorityQueue<String> pq = graph.get(pos);
        while(!pq.isEmpty()){
            String next = pq.poll();
            dfs(next);
        }
        postions.push(pos);
    }
    // 建图
    Map<String,PriorityQueue<String>> graph = new HashMap<>();
    public void buildGraph(List<List<String>> tickets){
        for(List<String> ticket : tickets){
            addEdge(ticket);
        }
    }
    public void addEdge(List<String> ticket){
        String from = ticket.get(0),to = ticket.get(1);
        addNode(from);
        addNode(to);

        graph.get(from).offer(to);
    }
    public void addNode(String pos){
        if(!graph.containsKey(pos)){
            graph.put(pos,new PriorityQueue<>());
        }
    }
}