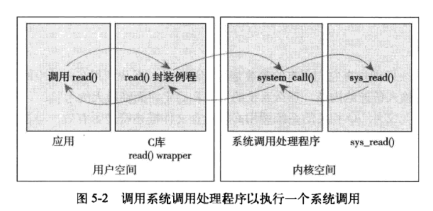
矩阵可视化

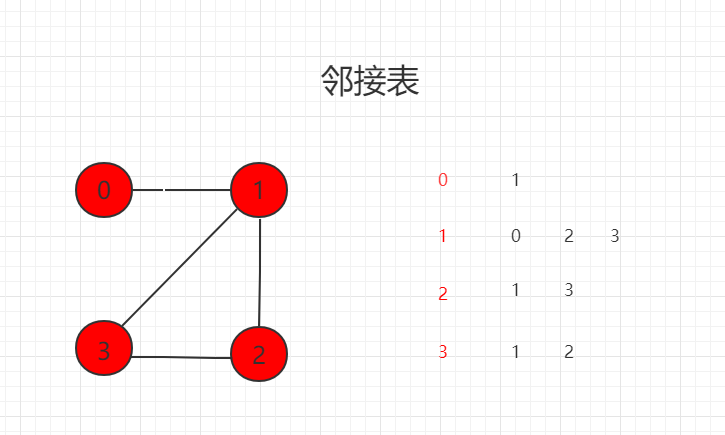
矩阵可以很方面地展示事物两两之间的关系，这种关系可以通过矩阵可视化的方式进行简单监控。

定义一个通用类

from matplotlib import pyplot as plt
import seaborn as sns
import numpy as np
import pandas as pd

class matrix_monitor():
    def __init__(self,min_color=-1,max_color=1,grad=5):
        self.min_color = min_color
        self.max_color = max_color
        self.grad = grad
        
    def fit_transform(self,Matrix):
        data = pd.DataFrame(Matrix)
        #设置色条的刻度：
        tick_=np.arange(self.min_color, self.max_color, self.grad).astype(float)

        #编辑做为参数的字典：
        dict_={'orientation':'vertical',"label":"color  \
        scale","drawedges":True,"ticklocation":"top","extend":"min", \
        "filled":True,"alpha":0.8,"cmap":"cmap","ticks":tick_}

        #将字典传入给参数cbar_kws:
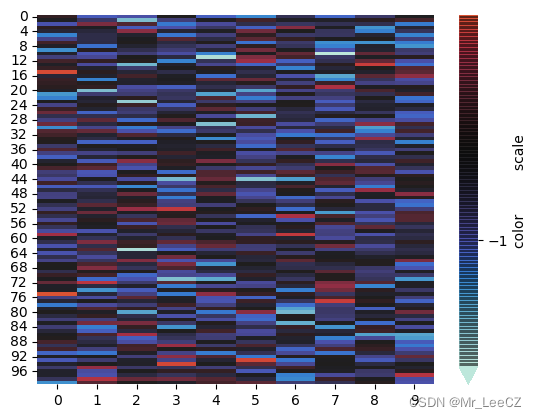
        cmap=sns.heatmap(data,cbar_kws=dict_,center=0.5)

        plt.show()

调用类

import numpy as np

X = data=np.random.randn(100,10)

model = matrix_monitor()
model.fit_transform(X)

结果展示