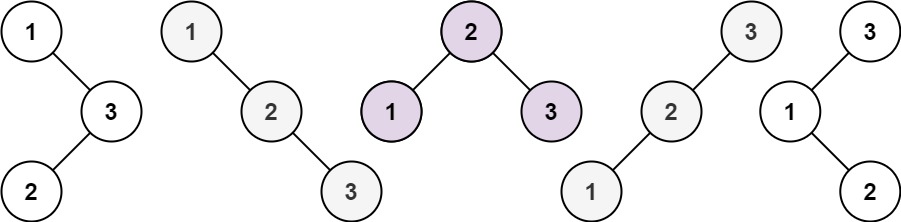
给你一个整数 n ，求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种？返回满足题意的二叉搜索树的种数。

 

       经典的面试题，这部分涉及了组合数学中的卡特兰数，如果对其不清楚的同学可以去看我以前的博客卡特兰数

今天用记忆化搜索以及动态规划进行讲解

• 记忆化搜索

    //维护一个记忆化搜素
    int[][] memo;
    public int numTrees(int n) {
     memo=new int[n+1][n+1];
    return  count(1,n);
    }
    public int count(int left,int right){
        //单节点，直接返回1
        if(left>=right){
            return 1;
        }
        if(memo[left][right]!=0){
            return memo[left][right];
        }
        int res=0;
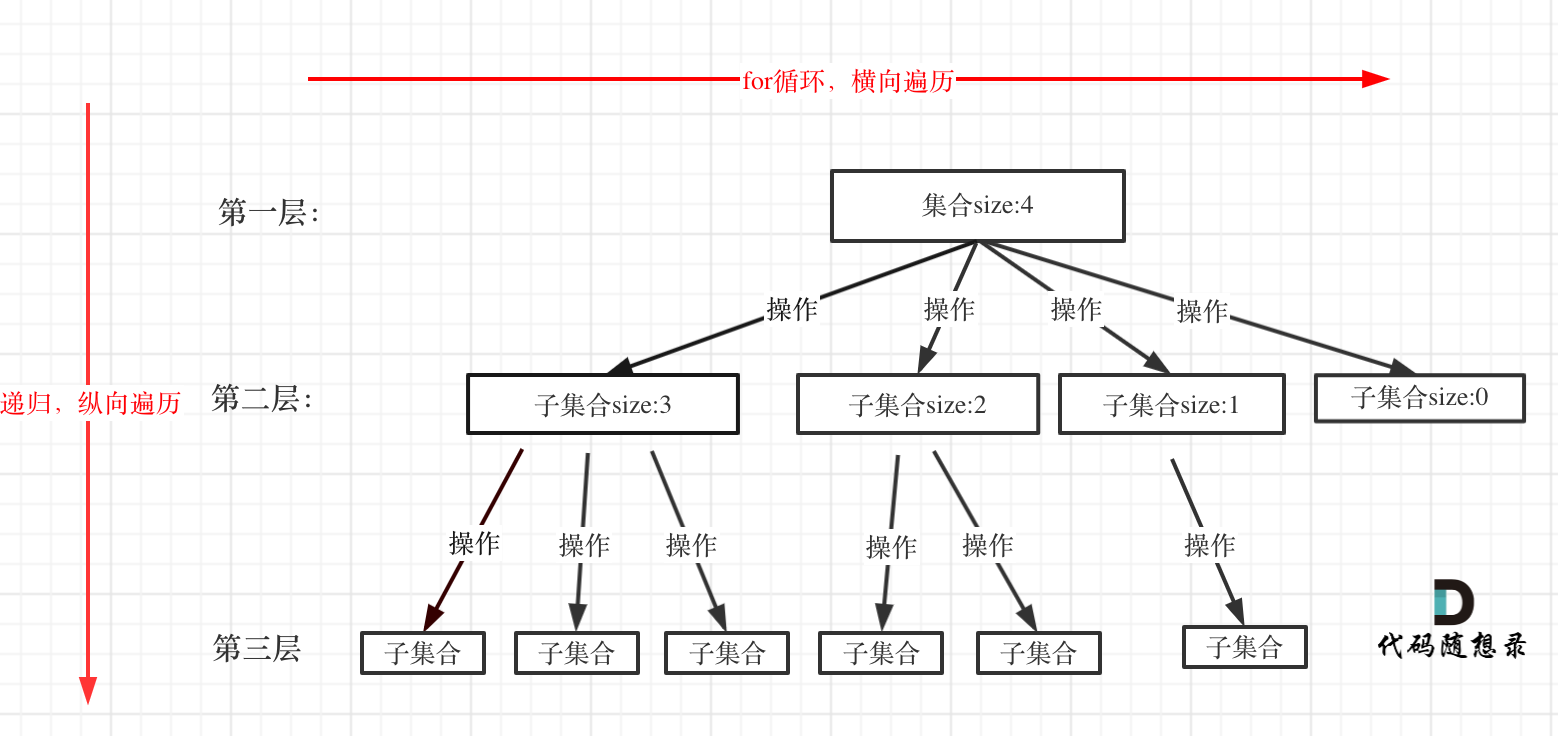
        //遍历区间内的每一个节点，都作为根节点的情况
        for(int mid=left;mid<=right;mid++){
            int l=count(left,mid-1);
            int r=count(mid+1,right);
            res+=l*r;
        }
        memo[left][right]=res;
        return res;
    }

• 动态规划

   public int numTrees(int n) {
    //先创建一个存储的数组
     int[] dp=new int[n+1];
     dp[0]=1;
        //节点可能存储的位置
        for (int i =1; i <=n; i++) {
            //左边节点可能存储的个数
            for (int j = 0; j<i; j++) {
                //计算出总种类  dp[j]是左树的节点个数 dp[i-j-1]是右树的节点个数
                dp[i]+=dp[j]*dp[i-j-1];
            }
        }
     return dp[n];
        }