二分查找也称折半查找(Binary Search),是一种效率较高的查找方法,时间复杂度为O(logN)。
二分查找采用了“分治”策略。使用二分查找时,数组中的元素之间得有单调性(升序或者降序)。
二分的模板据我目前所知有三个,但是下面是我个人认为最好的一种(比较简单,不容易写错~)
1. 整数二分
整数二分过程:
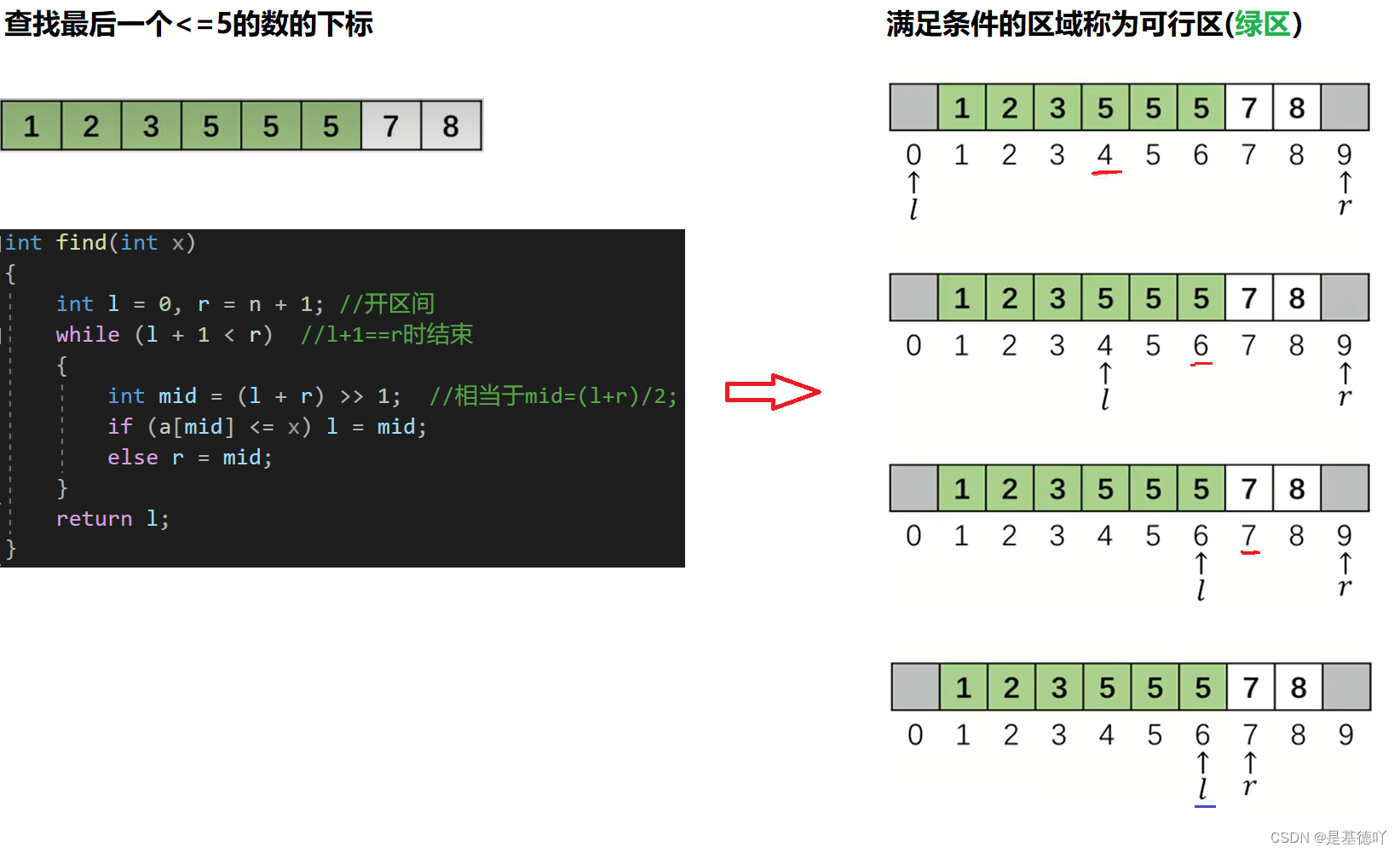
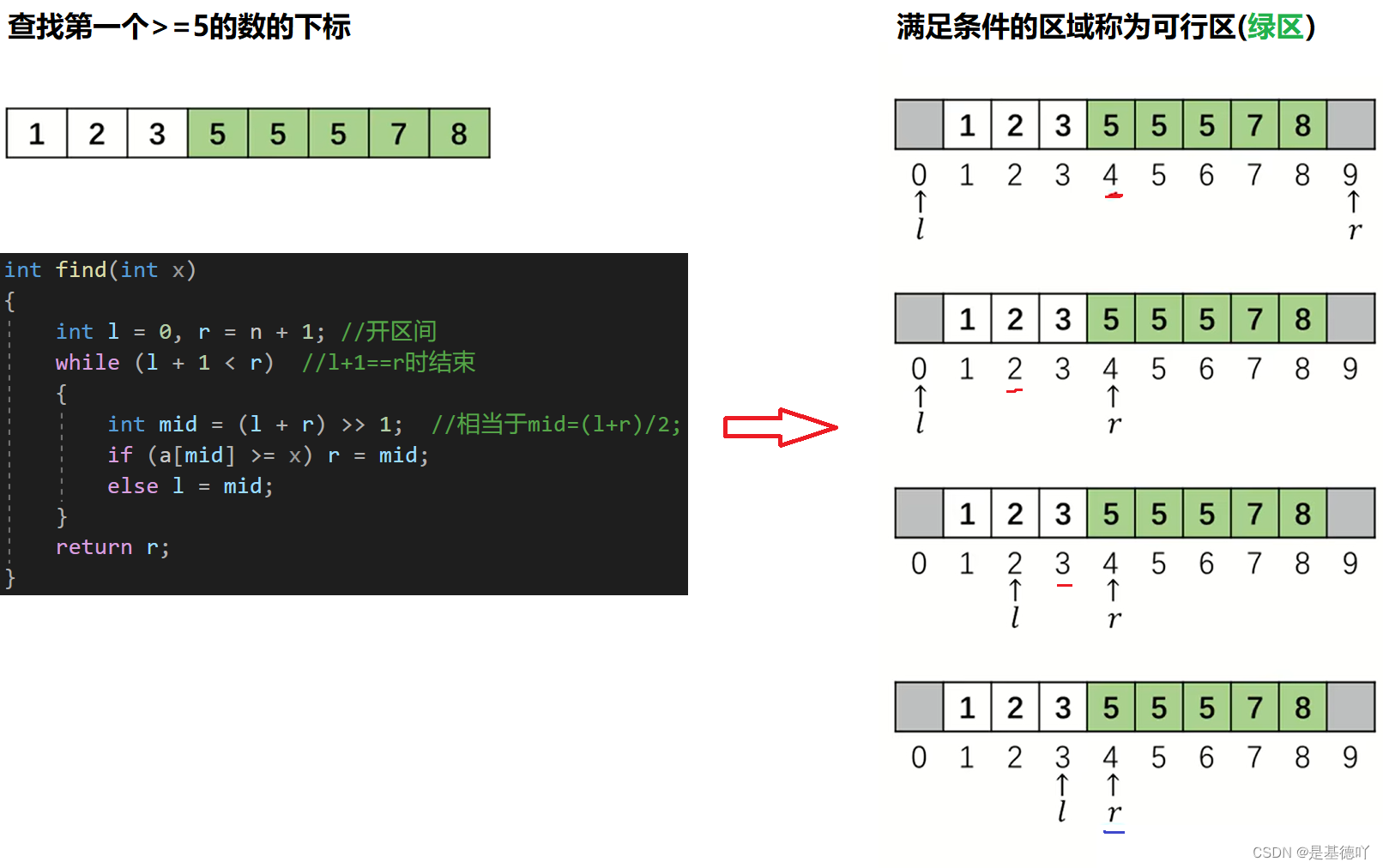
普遍规律:
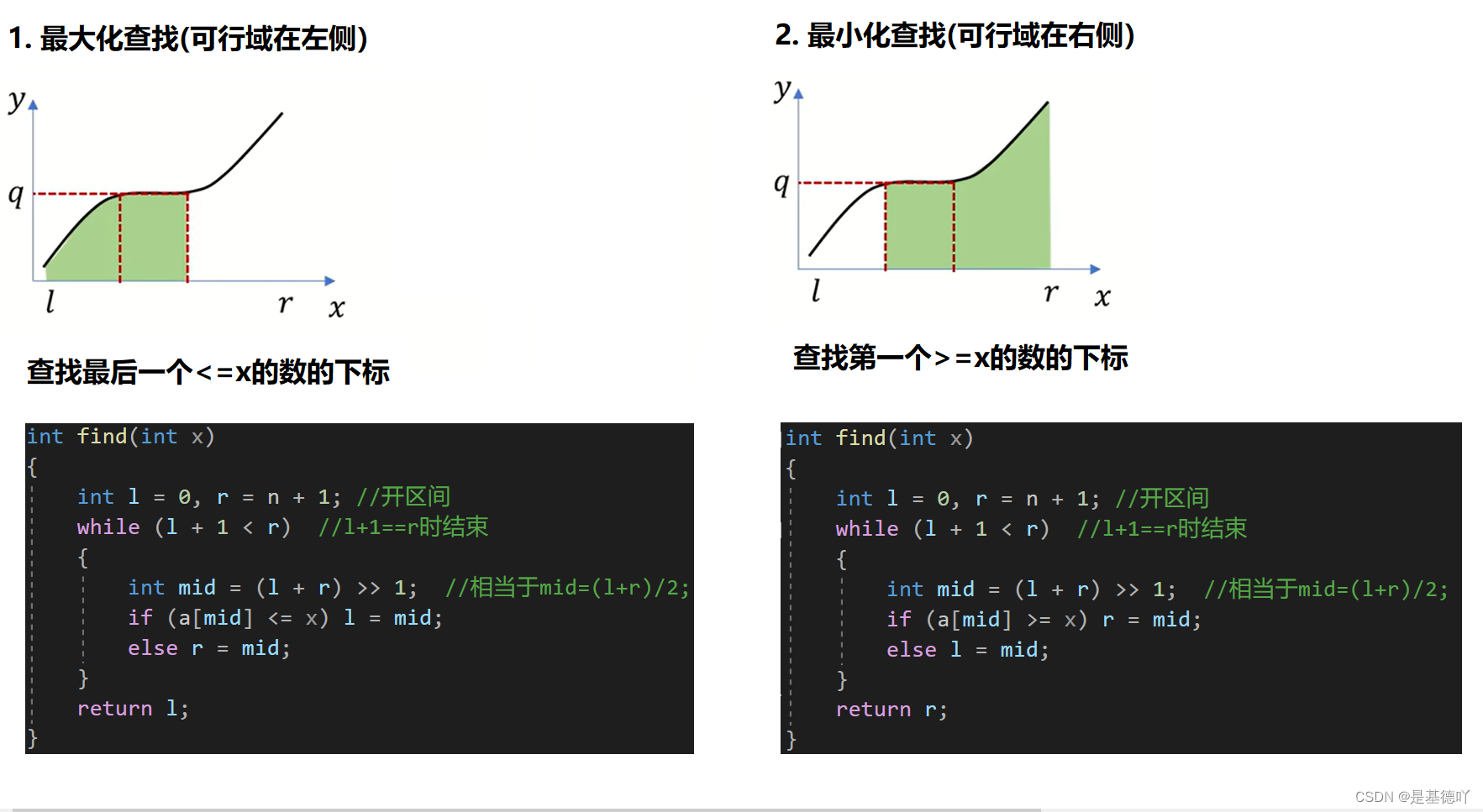
我们发现:

2. 整数二分模板
查找最后一个<=x的数的下标:
int find(int x)
{
int l = 0, r = n + 1; //开区间
while (l + 1 < r) //l+1==r时结束
{
int mid = (l + r) >> 1; //相当于mid=(l+r)/2;
if (a[mid] <= x) l = mid;
else r = mid;
}
return l;
}查找第一个>=x的数的下标:
int find(int x)
{
int l = 0, r = n + 1; //开区间
while (l + 1 < r) //l+1==r时结束
{
int mid = (l + r) >> 1; //相当于mid=(l+r)/2;
if (a[mid] >= x) r = mid;
else l = mid;
}
return r;
}3. 整数二分模板题
3.1 洛谷P2249 【深基13.例1】查找
原题链接:https://www.luogu.com.cn/problem/P2249

#define _CRT_SECURE_NO_WARNINGS 1
#include<bits/stdc++.h>
using namespace std;
const int N = 1e6 + 10;
int a[N], n, m;
int find(int x)
{
int l = 0, r = n + 1;
while (l + 1 < r)
{
int mid = (l + r) >> 1;
if (a[mid] >= x) r = mid;
else l = mid;
}
if (a[r] == x) return r;
else return -1;
}
int main()
{
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++) scanf("%d", &a[i]);
while (m--)
{
int k;
scanf("%d", &k);
printf("%d ", find(k));
}
return 0;
} 3.2 Acwing789. 数的范围
3.2 Acwing789. 数的范围
原题链接:https://www.acwing.com/problem/content/791/

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int a[N],n,q;
int find1(int x)
{
int l=-1,r=n;
while(l+1<r)
{
int mid=(l+r)>>1;
if(a[mid]>=x) r=mid;
else l=mid;
}
if(a[r]==x) return r;
else return -1;
}
int find2(int x)
{
int l=-1,r=n;
while(l+1<r)
{
int mid=(l+r)>>1;
if(a[mid]<=x) l=mid;
else r=mid;
}
if(a[l]==x) return l;
else return -1;
}
int main()
{
scanf("%d%d",&n,&q);
for(int i=0;i<n;i++) scanf("%d",&a[i]);
while(q--)
{
int k;
scanf("%d",&k);
printf("%d %d\n",find1(k),find2(k));
}
}4. 浮点数二分
我们看下图:

分析:
(其实是个二分答案的题目)
y=x^3,我们知道这是个单调递增的函数。
-10000开三次方根大概是-27,10000开三次方根大概是27。
因为-10000<=y<=10000,我们为了方便,把左边界设置成-100,右边界设置成100。

我们可以直观看到-27~27包含在-100~100。所以这样设置左右边界是没有问题滴。
我们不断二分缩小范围,当l和r非常接近时(r-l<=1e-8),我们就认为找到了这个三次方根。
否则我们用while(r-l>=1e-8)继续循环遍历。
又因为是递增的,所以mid*mid*mid<=y,我们让区间往右靠(l=mid);反之,当mid*mid*mid>y时,我们让区间往左靠(r=mid)。
最后返回左边界l即可。
5. 浮点数二分模板
double find(double y)
{
double l = -100, r = 100;
while (r - l > 1e-8)
{
double mid = (l + r) / 2;
if (mid * mid * mid <= y) l = mid;
else r = mid;
}
return l;
}6. 浮点数二分模板题
6.1 Acwing 790.数的三次方根
原题链接:https://www.acwing.com/problem/content/792/

#include<bits/stdc++.h>
using namespace std;
double n;
int main()
{
scanf("%lf", &n);
double l = -100, r = 100;
while (r - l > 1e-8)
{
double mid = (l + r) / 2;
if (mid * mid * mid <= n) l = mid;
else r = mid;
}
printf("%.6lf\n", r);
return 0;
}