前言

（1）在学习数据结构链表部分的时候，老师给出了几个题目。其中两个题目采用了快慢指针的技术，感觉有意思，于是写一篇博客记录一下。

快慢指针

（1）我们先来介绍一下快慢指针技术。这个说起来其实很简单，就是龟兔赛跑问题。
（2）兔子跑的比乌龟快，我们可以利用这个特性，来解决一些实际按理。

求链表的中间结点

原题链接

（1）原题链接：https://leetcode.cn/problems/middle-of-the-linked-list/description/

分析

（1）此题的核心目标是找到单链表的中间节点。如果是顺序表，就非常简单，直接采用sizeof()知道顺序表的大小，然后直接访问就可以了。
（2）但是单链表的存储不是连续的，想要找到某个元素，必须从头寻找。
（3）从头寻找又会有一个问题，因为这里是单链表，你只能往前走，不能回退。所以就算你遍历了整个链表，知道了链表的长度之后，还需要从头遍历链表，找到中间位置返回。假设这个链表长度是N，那么你就需要遍历1.5N次。
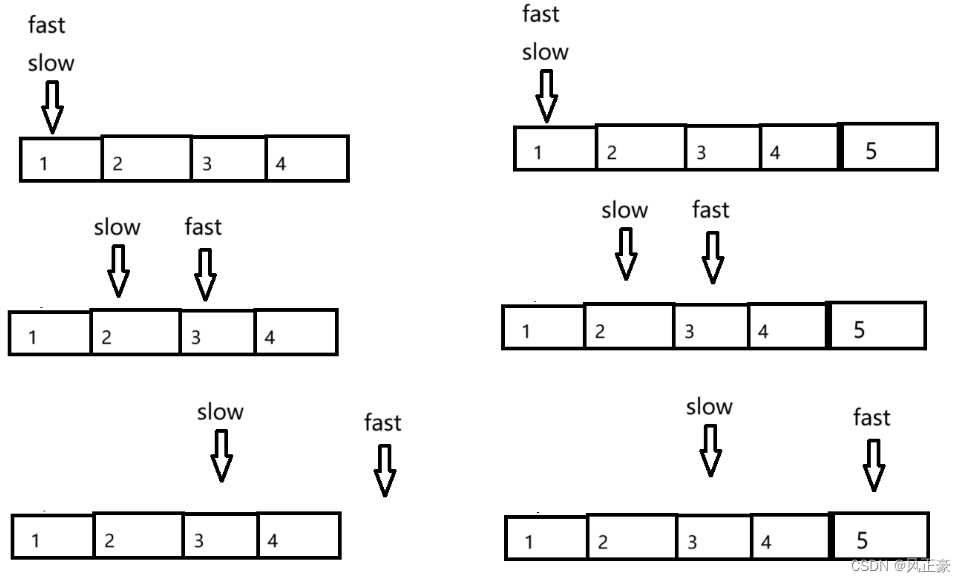
（4）这样虽然可行，但是很麻烦，因此我们可以采用快慢链表的方式，很好的解决这个问题。为什么这么说呢？因为我们需要找到单链表的中间位置，于是可以建立一个速度是乌龟一倍的兔子，如果兔子跑到了终点了，那么乌龟就正好是在中间位置。因此我们看下面这张图分析：
<1>假设这个单链表是偶数个，按照下面这个流程来，我们会发现跑的快的兔子最终会跑出赛道，而乌龟正好是在中间位置的第二个节点，完美符合要求。因此，单链表为偶数个，结束条件为fast==NULL。
<2>假设单链表是奇数个，按照下面流程来看，我们可以知道，兔子正好跑到终点，再跑就跑出赛道了。因此，单链表为奇数个，结束条件为fast–>==NULL。

在这里插入图片描述

代码

根据上面的解析，我们可以写出下面这段代码

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     struct ListNode *next;
 * };
 */


struct ListNode* middleNode(struct ListNode* head){
    struct ListNode* slow = head,*fast = head;
    while(fast != NULL && fast->next !=NULL)
    {
        slow = slow->next;
        fast = fast->next->next;
    }
    return slow;
}

判断链表是否是环形链表

原题链接

原题链接：https://leetcode.cn/problems/linked-list-cycle/description/

分析

（1）这个链表可能是一个环，我们需要进行判断，那么我们可以让兔子和乌龟在这个赛道里面跑。因为兔子比乌龟的速度快，所以这个环赛道里面，兔子铁定可以追上乌龟的。

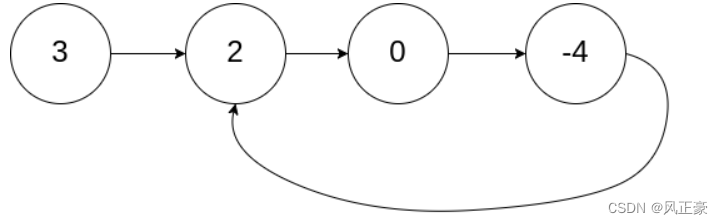
在这里插入图片描述

（2）但是，各位需要注意一个点，只要时间足够，兔子在这个赛道一定可以追上乌龟。可是，兔子追上了乌龟一定会停下来吗？
（3）为什么需要问这个问题呢？因为，我们在编程的时候，都是先让兔子和乌龟跑一次，然后判断乌龟和兔子位置是否重叠。如果兔子和乌龟位置重叠，那么说明这是一个环形链表，如果兔子一直跑，发现能够跑到尽头，那么就说明这不是一个环形链表。
（4）那么我们想一下，如果这是一个环形链表，时间足够，兔子是肯定可以追上乌龟的，但是在进行判断的时候，兔子和乌龟的速度会重合吗？
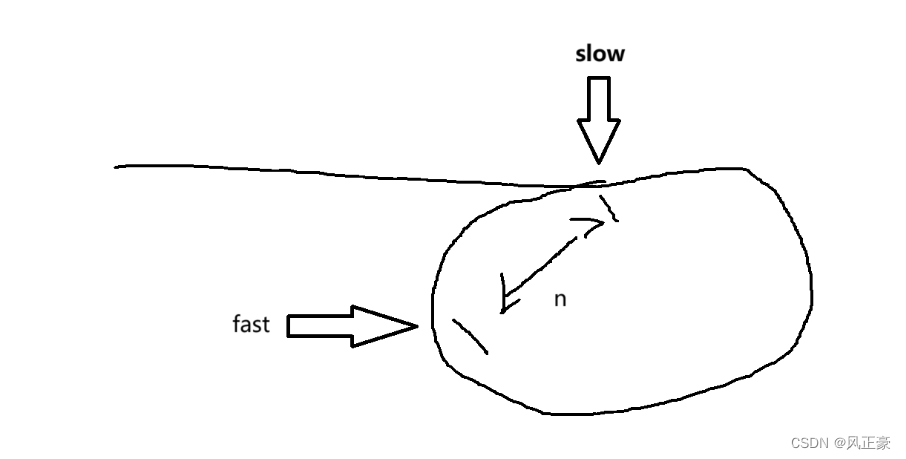
（5）为了解决这个问题，我们可以画出下面这张图：
<1>假设乌龟进入环形区了，兔子肯定在这里面跑了一段时间了，现在是兔子追乌龟的过程。这个时候兔子距离乌龟n个元素。
<2>分析到这里，这个问题就很简单了，说白了就是一个小学的数学问题。因为兔子比乌龟速度要快，所以我们可以假设乌龟是不运动的，兔子的速度就是比乌龟快的那一部分。
<3>假设乌龟速度是每次走1个元素，兔子是每次走2个元素。那么按照上面分析，让乌龟不动，兔子移动，那么兔子的速度就是每次走一个元素。
<4>最终兔子走n次可以追上乌龟。

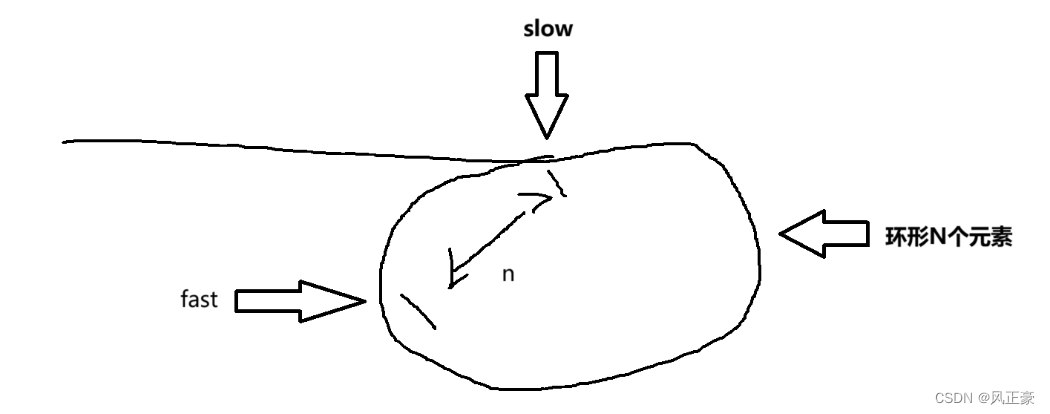
在这里插入图片描述

（6）看了上面的分析，肯定有同学会想，我们可不可以让兔子的速度比乌龟的再快一点呢？我要让乌龟的速度是1，兔子速度是3呢？
<1>现在我们假设这张图的环形是N个元素，乌龟到底环形区的时候，兔子距离乌龟n个元素。为了防止兔子追上了乌龟，但是越过了他，因此我们假设兔子要跑k圈最终才能和乌龟位置重合。
<2>根据上面的假设，我们可以建立下面这个数学模型计算出兔子要跑多少次才能追上乌龟。注意，k可以是0，1，2…的任意整数
$\frac{k*N+n}{fast-slow}$
<3>我们一直尝试k的值，最终计算出来的最小整数，就算兔子要跑的次数。
<4>上面我们假设了兔子每次跑3个元素，乌龟每次跑1个元素。因此fast-slow就是2。
<5>我们假设这个环形区N为4，乌龟到达环形区时候，兔子距离他的n为1。那么套入公式就是
$\frac{k*N+n}{fast-slow} = \frac{k*4+3}{2}= 2*k + 1.5$
<6>发现没有，上面这个条件下，永远不可能算出整数。因此，兔子比乌龟的速度快1个元素才能解决所有可能情况。
<7>这个时候，肯定又有人要说了，那我让兔子比乌龟的速度快1个元素，但是我让乌龟的速度提上来可以不。可以，当然可以，但是不推荐，你速度提上来了，但是程序运行速度就不一定提上来了，因为你乌龟看起来每次是多走了一点距离，但是对于程序而言，还是一步一步的走，不过不是每步都进行了一次判断而言。

在这里插入图片描述

代码

（1）根据上面的分析，我们可以写出如下代码

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     struct ListNode *next;
 * };
 */
bool hasCycle(struct ListNode *head) {
    struct ListNode* slow = head,*fast = head;
    while(fast != NULL && fast->next != NULL)
    {
        slow = slow->next;
        fast = fast->next->next;
        if(slow==fast)
        {
            return true;
        }
    }
    return false;
}