目录

199. 二叉树的右视图

题解：

目标：

思路：

过程：

代码：

运行结果：

---

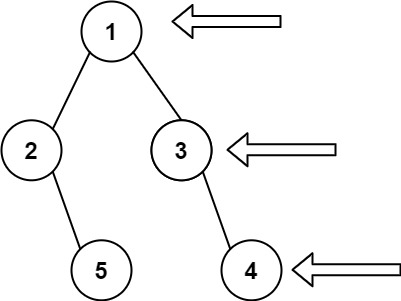
给定一个二叉树的 根节点 root，想象自己站在它的右侧，按照从顶部到底部的顺序，返回从右侧所能看到的节点值。

示例 1:

输入: [1,2,3,null,5,null,4]
输出: [1,3,4]

示例 2:

输入: [1,null,3]
输出: [1,3]

示例 3:

输入: []
输出: []

提示:

• 二叉树的节点个数的范围是 [0,100]
• -100 <= Node.val <= 100  

题解：

目标：

从二叉树的右侧观察，返回能够看到的节点值列表，即红色部分

 （图片采用力扣官网解题图示）

思路：

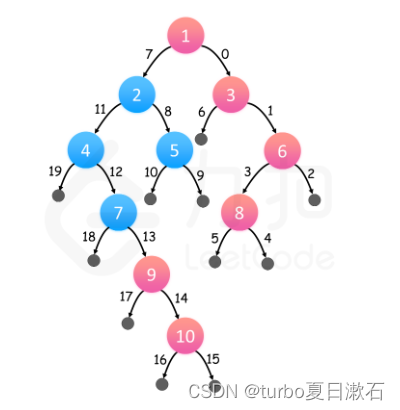
对树进行深度优先遍历，采用根右左的顺序，总是先访问右子树。那么对于每一层来说，我们在这层见到的第一个结点一定是最右边的结点。

所以如果存储在每个深度访问的第一个结点，一旦我们知道了树的层数，就可以得到最终的结果数组。

过程：

1. 首先，我们需要定义一个辅助函数 dfs 来进行深度优先搜索。该函数接收当前节点 root 和当前层数 dep 作为参数。
2. 在 dfs 函数中，我们首先判断当前节点是否为空，如果为空则直接返回。这是终止条件。
3. 接下来，我们判断当前层数 dep 是否大于已记录的最大层数 depth。如果是，则说明当前层是从右侧观察第一次能够看到的节点，将其值添加到结果列表 res 中，并更新最大层数 depth。
4. 然后，我们递归调用 dfs 函数，在右子节点上进行深度优先搜索，传入当前层数加 1 的值作为参数。
5. 再次递归调用 dfs 函数，在左子节点上进行深度优先搜索，同样传入当前层数加 1 的值作为参数。
6. 最后，返回结果列表 res。

代码：

class Solution {
    // 记录结果
    List<Integer> res=new ArrayList<>();
    // 辅助记录树的层数
    int depth=-1;
    public List<Integer> rightSideView(TreeNode root) {
        if (root == null) return res; // 处理根节点为空的情况
        dfs(root,0);
        return res;
    }
    public void dfs(TreeNode root,int dep){
        if(root==null) return;
        if(depth<dep){
            res.add(root.val);
            depth++; 
        }
        dfs(root.right,dep+1);
        dfs(root.left,dep+1);
        return;
    }
}

运行结果：