题目

设计一个算法，找出数组中最小的k个数。以任意顺序返回这k个数均可。

示例

输入： arr = [1,3,5,7,2,4,6,8], k = 4
输出： [1,2,3,4]

提示

0 <= len(arr) <= 100000
0 <= k <= min(100000, len(arr))

开始解题

1.思路

建立小根堆,遍历这个数组把数组中的元素都放到小根堆中
定义一个数组ret作为返回值,,取k次堆顶元素放到数组中,返回ret

2.解题代码

public class Solution {
    /*
     * 这样写的话效率不是很高
     * */
    public int[] smallestK(int[] arr, int k) {
        int[] ret= new int[k];
        if(arr==null||k==0){
            return null;
        }
        //向上调整来建堆,时间复杂度为 O(N*logN)
        Queue<Integer> minHeap = new PriorityQueue<>();
        for (int i : arr) {
            minHeap.offer(i);
        }
        //poll() 移除优先级最高的元素并返回，如果优先级队列为空，返回null
        //每一次移除堆顶元素,都必须进行向下调整这棵二叉树,假设树的高度为h,时间复杂度log(h)
        //再加上循环k次,这段代码的时间复杂度为O(K * logH)
        for (int i = 0; i < k; i++) {
            ret[i]=minHeap.poll();
        }
        return ret;
    }
}

3.时间复杂度

//向上调整来建堆,时间复杂度为 O(N*logN)
Queue<Integer> minHeap = new PriorityQueue<>();
for (int i : arr) {
minHeap.offer(i);
}
//poll() 移除优先级最高的元素并返回，如果优先级队列为空，返回null
//每一次移除堆顶元素,都必须进行向下调整这棵二叉树,假设树的高度为h,时间复杂度log(h)
//再加上循环k次,这段代码的时间复杂度为O(K * logH)
for (int i = 0; i < k; i++) {
ret[i]=minHeap.poll();
}

所以上述解法的时间复杂度为:O(N*logN+K * logH)

4.运行结果

目前问题

代码运行效率不高,时间复杂度不行,太高了

主要原因

//向上调整来建堆,时间复杂度为 O(N*logN)
Queue<Integer> minHeap = new PriorityQueue<>();
for (int i : arr) {
minHeap.offer(i);
}
//poll() 移除优先级最高的元素并返回，如果优先级队列为空，返回null
//每一次移除堆顶元素,都必须进行向下调整这棵二叉树,假设树的高度为H,由节点总数与树的高度关系可得:N=2^H-1=>H=log(N+1)
//再加上循环k次,这段代码的时间复杂度为O(K*logN)
for (int i = 0; i < k; i++) {
ret[i]=minHeap.poll();
}

真正的解法

TOP-K问题：即求数据集合中前K个最大的元素或者最小的元素

TOP-K问题并不是将全部数据建立成堆,因为TOP-K问题一般情况下数据量都比较大。

真正的解法:是拿前K个建堆;找前K个最小的元素,建一个大根堆;找前K个最大的元素,建一个小根堆

TOP-K主要指的是在很大的一组数据的背景下进行,前K个元素仅仅只占很小的一部分,所以建堆和调整堆的时间复杂度也就变得很小了

1.以找前K个最大的元素为例

输入： arr = [27,15,19,18,28], k = 3

2.代码执行过程&&时间复杂度的计算

1.建立一个大小为K的小根堆(构造器默认的),没放元素,本质上是建立了一个大小为K的数组

2.遍历数组的前K个,放到小根堆minHeap当中 => 向上调整建堆
时间复杂度: K*logK

3.遍历剩下的K-1个,每次和堆顶元素进行比较
(1)如果该元素比堆顶元素小说明该元素一定不是前K个最大元素中的值，就不入堆;
(2)如果该元素比堆顶元素大堆,则该元素与堆中最后个元素交换,再移除最后一个元素再把该元素入堆,
入到最后一个先素的位置,调整该完全二叉树,使其再次成为个小根堆;
时间复杂度:(N-K)*H=>(N-K)logK 注:(H为树的高度,K=2^H-1,H=log(K+1))
(N-K)*H=>(N-K)*log(K+1)=>(N-K)logK

4.将堆中的元素放到ret里面,每次poll都是弹出堆中的最小值
时间复杂度: K*logK

所以时间复杂度: K*logK+(N-K)*logK+ K*logK => N*logK + K*logK
取近似值:O(N*logK) 注:K为常数,可忽略不计

3.画图演示代码执行过程

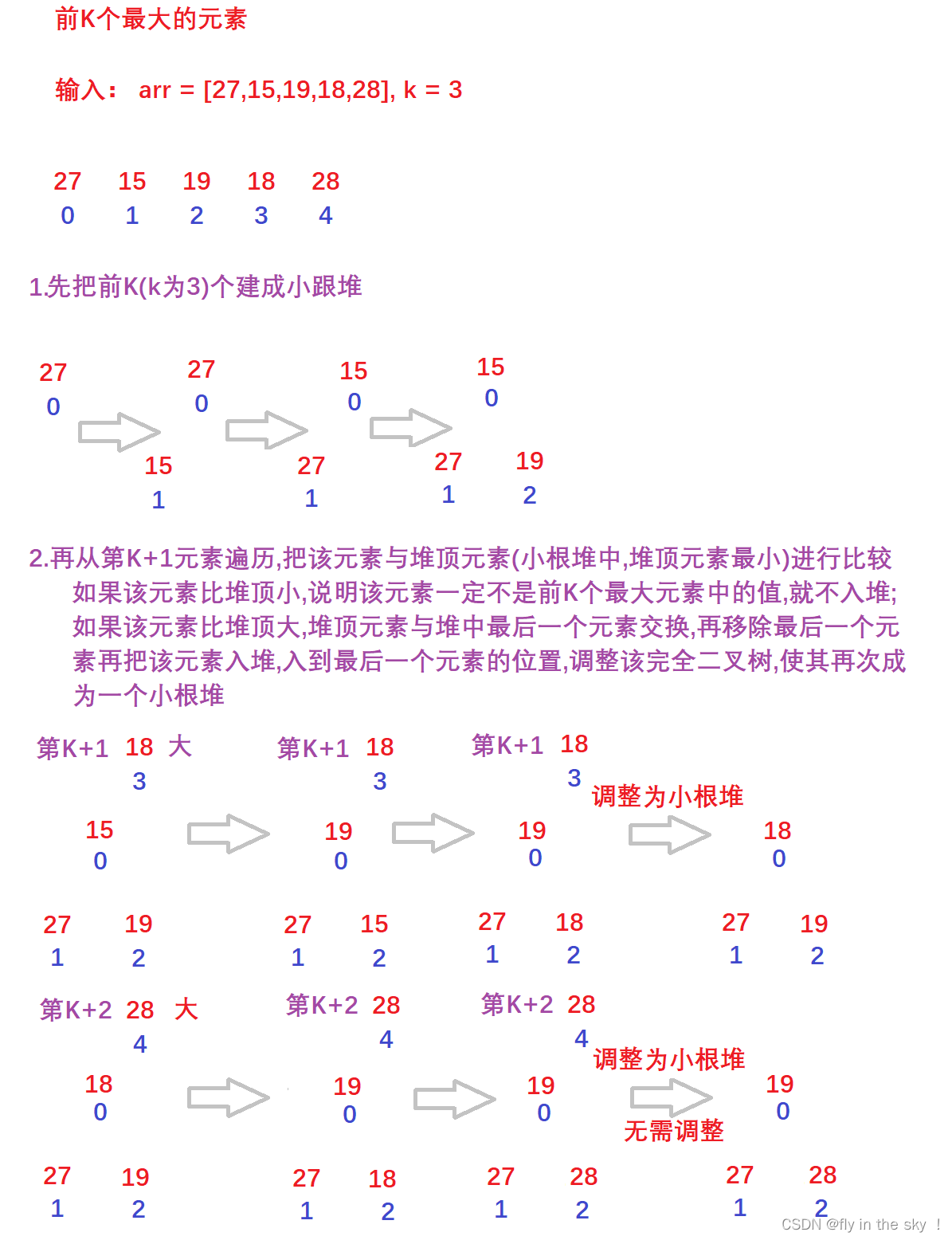
注:

小根堆中是前K个最大的值
堆顶元素是这K个最大的值里面最小的
最后的堆顶元素就是第K大的元素(牢记,面试官可能会问到!!!)
当遍历到数组元素大于堆顶的时候，说明此时堆顶的元素一定不是前K个最大的值

4.解题代码

    /*
    * 前k个最大的元素
    * 时间复杂度:K*logK
    * */
    public static int[] largestK(int[] arr, int k) {
        int[] ret = new int[k];
        if (arr==null||k==0){
            return null;
        }
        //1.建立一个大小为K的小根堆(构造器默认的),没放元素,本质上是建立了一个大小为K的数组

        Queue<Integer> minHeap = new PriorityQueue<>(k);
        //2.遍历数组的前K个,放到小根堆minHeap当中
        //时间复杂度: K*logK+(N-K)logK+ K*logK
        //取近似值:O(N*logK)
        for (int i = 0; i < k; i++) {
            minHeap.offer(arr[i]);
        }
      /* 3.遍历剩下的K-1个,每次和堆顶元素进行比较
        (1)如果该元素比堆顶元素小说明该元素一定不是前K个最大元素中的值，就不入堆;
        (2)如果该元素比堆顶元素大堆,则该元素与堆中最后个元素交换,再移除最后一个元素再把该元素入堆,
        入到最后一个先素的位置,调整该完全二叉树,使其再次成为个小根堆*/
        //时间复杂度:(N-K)*H=>(N-K)logK
        //注:(H为树的高度)K=2^H-1,H=log(K+1)
        //(N-K)*H=>(N-K)*log(K+1)=>(N-K)logK
        for (int i = k; i <arr.length ; i++) {
            int heapTop = minHeap.peek();
            if (arr[i]>heapTop){
                minHeap.poll();
                minHeap.offer(arr[i]);
            }
        }
        //4.将堆中的元素放到ret里面,每次poll都是弹出堆中的最小值
        //时间复杂度: K*logK
        for (int i = 0; i < k; i++) {
            ret[i]=minHeap.poll();
        }
        return ret;
    }