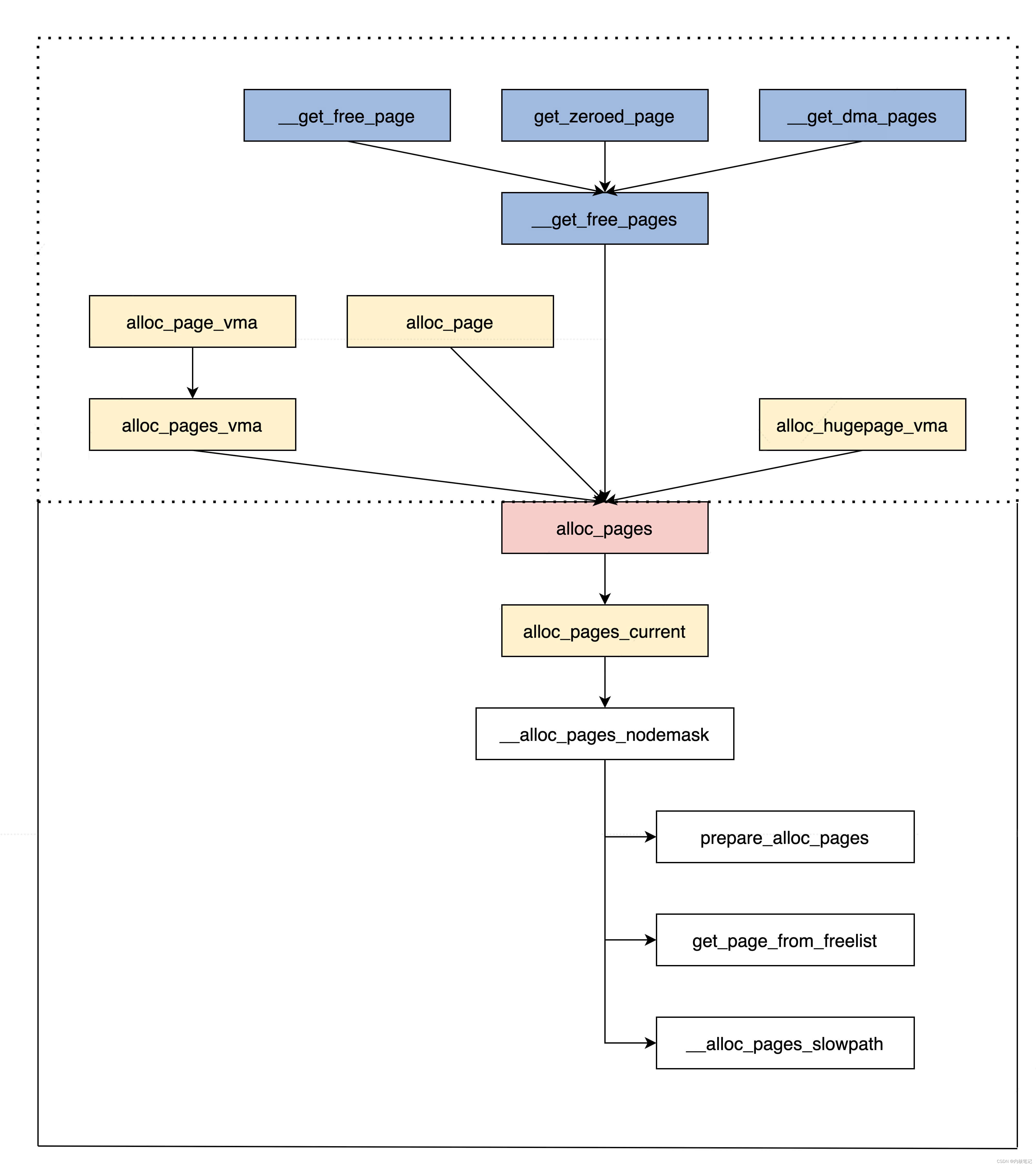
题目描述

矩形以列表 [x1, y1, x2, y2] 的形式表示，其中 (x1, y1) 为左下角的坐标，(x2, y2) 是右上角的坐标。矩形的上下边平行于 x 轴，左右边平行于 y 轴。

如果相交的面积为正，则称两矩形重叠。需要明确的是，只在角或边接触的两个矩形不构成重叠。

给出两个矩形 rec1 和 rec2 。如果它们重叠，返回 true；否则，返回 false 。

示例 1：

输入：rec1 = [0,0,2,2], rec2 = [1,1,3,3]
输出：true

示例 2：

输入：rec1 = [0,0,1,1], rec2 = [1,0,2,1]
输出：false

示例 3：

输入：rec1 = [0,0,1,1], rec2 = [2,2,3,3]
输出：false

提示：

rect1.length == 4
rect2.length == 4
-109 <= rec1[i], rec2[i] <= 109
rec1 和 rec2 表示一个面积不为零的有效矩形

解题思路

方法一

假设有矩形rec1, rec2，在二维坐标系中的如果rec1和rec2不重叠，则rec1肯定在rec2的左侧或右侧或上侧或下侧，如图：

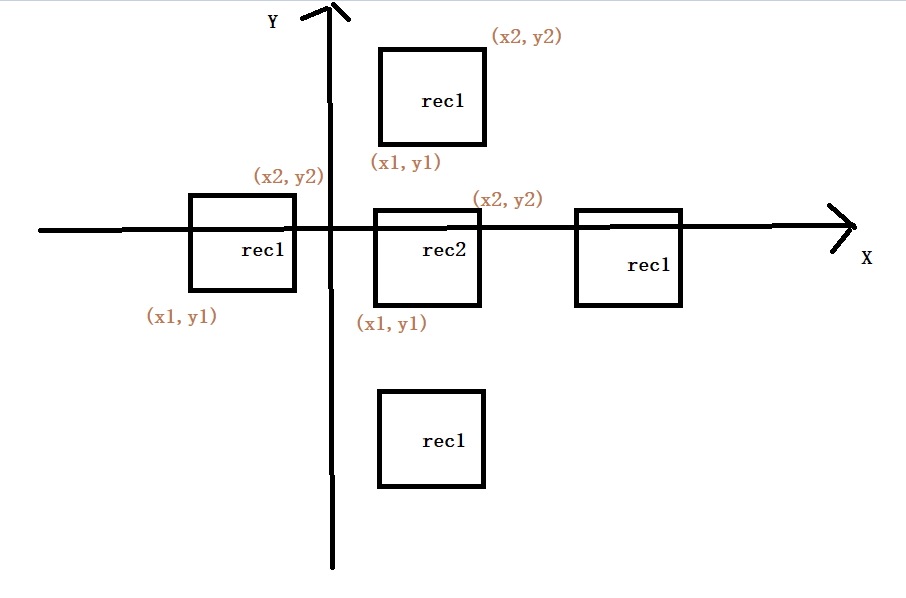如果rec1在rec2的左侧，则rec1的x2<=rec2的x1。

如果rec1在rec2的上侧，则rec1的y1>=rec2的y2。

如果rec1在rec2的右侧，则rec1的x1>=rec2的x2。

如果rec1在rec2的下侧，则rec1的y2<=rec2的y1。

说明：rec1在rec2的左侧相当于rec2在rec1的右侧。

代码：

public boolean isRectangleOverlap(int[] rec1, int[] rec2) {
    return !(rec1[2] <= rec2[0] || rec1[1] >= rec2[3] || rec1[0] >= rec2[2] || rec1[3] <= rec2[1])
}

方法二

将两个矩形在x轴和y轴投影，如果不重叠，则投影的情况如图：

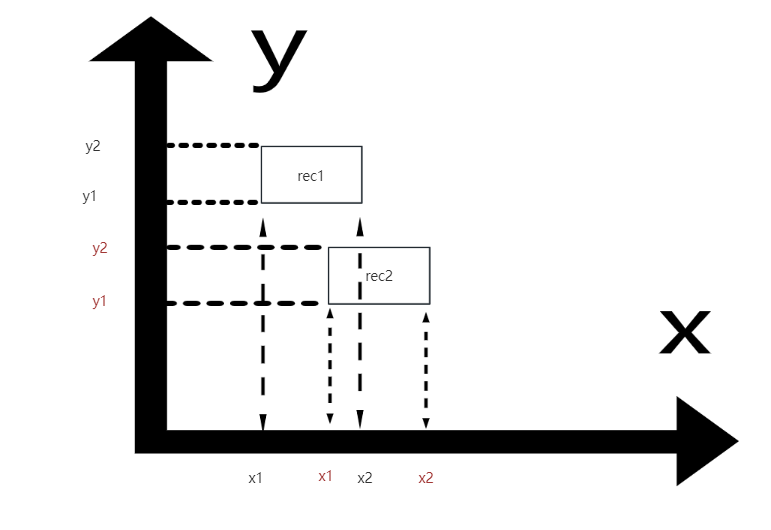
对于x轴上的投影线段rec1(x1,x2), rec2(x1,x2)和y轴上的投影线段rec1(y1,y2)，rec2(y1,y2)，如果两组线段都相交，则说明两个矩形重叠。

判断两个线段是否相交：min(rec1[2], rec2[2]) > max(rec1[0], rec2[0])。

代码：

public boolean isRectangleOverlap(int[] rec1, int[] rec2) {
    return !(rec1[2] <= rec2[0] || rec2[2] <= rec1[0]) && !(rec2[1] >= rec1[3] || rec1[1] >= rec2[3]);
}