基于OpenGL的地形建模技术的研究与实现

诚信声明

本人郑重声明：本设计（论文）及其研究工作是本人在指导教师的指导下独立完成的，在完成设计（论文）时所利用的一切资料均已在参考文献中列出。

本人签名：年月日

毕业设计（论文）任务书

毕业设计（论文）题目：基于OpenGL的地形建模技术的研究与实现

课题意义及目标
地形建模是游戏开发的基础。本课题要求使用OpenGL开发一个以三角形网格划分的具有贴图纹理映射的三维地形。
主要任务
学习四叉树构建地形；消除四叉树裂缝；对地形实现纹理贴图；地形高度使用灰度图片实现；
预期成果：开发一个等均匀度的地形；如果能纳入LOD技术就达到了更高的要求。
主要参考资料

[1] 柯希林,曾军.动态LOD四叉树虚拟地形绘制[J].测绘通报,2005,(06):10.

[2] 潘李亮,基于LOD的大规模真实感室外场景实时渲染技术的初步研究[J].西安工业大学软件学院,2009,(04):112-115.

[3] 王宏武,董士海.一个与视点相关的动态多分辨率地形模型[J].计算机辅助设计与图形学学报,2000,(08):05-06.

4．进度安排

	设计（论文）各阶段名称	起止日期
1	学习OpenGL，建立OpenGL运行环境	12月15日～12月30日
2	学习四叉树数据结构，建立四叉树地形框架	01月01日～02月28日
3	学习四叉树数据结构构造，编写地形网格	03月01日～03月31日
4	对网格进行渲染贴图，纹理映射，模块测试	04月01日～05月15日
5	撰写论文	05月16日～06月22日

审核人：年月日

基于OpenGL的地形建模技术的研究与实现

摘要

为了旅游区规划以及游戏对地形方面的开发需求，本文围绕“地形”这个话题展开。生成地形的方法有分形生成地形，多边形模拟算法，曲面拟合地形仿真算法。本文分别采用分形生成和四叉树算法来绘制地形。首先解释了高度是一个存储了二维数组的地形文件，然后利用两种算法来构建地形，分形生成地形通过diamond-square算法来生成地形，四叉树则通过节点信息对高度图中的数据进行索引来形成地形，并且采用在裂缝中增加一条边的方法对产生的裂缝进行修补。最后对地形进行纹理贴图，将所有的纹理都绘制在一张图上，再指派对应纹理坐标进行渲染。

通过对以上方法的对比，四叉树具有层次的结构要比分形的正三角形结构绘制效率高，四叉树形成一个连续平滑且具有动态的层次细节的多分辨率地形，使场景更加逼真。

关键词：地形建模，OpenGL ，高度图，分形，四叉树

Research and Implementation of Terrain Modeling Technology Based on OpenGL

Abstract

When it comes to tourism plan meet the terrain's development requirements of game, the paper is expounded around the topic of "terrain".Methods of generating terrain includes fractal generation terrain,polygon simulation algorithm, surface fitting terrain simulation algorithms. The paper uses fractal generation and quad-tree algorithm to draw the terrain. Firstly, the paper explains that the height is the terrain file to store two-dimensional array, and then build the terrain by two algorithms. The fractal generation terrain generates terrain by using diamond-square algorithm and quad-tree algorithm forms terrain through node information indexing the data in the height map, and repairs cracks by the way of increasing one edge in the crack. Finally, the texture for the terrain should be mapped. All the textures are plotted on a graph and then assign the corresponding the texture coordinates for rendering.

By contrasting to the above method, the regular structure of quad-tree is more efficient to draw than fractal triangle structure. The quad-tree algorithm forms a terrain which is continuous,smooth,dynamic and detailed multi-resolution,it makes the scene more realistic.

Keywords: Terrain modeling, OpenGL , height map , Fractal , quad tree

1 绪论11

1.1 课题研究目的及意义11

1.1.1 课题研究的目的11

1.1.2 课题研究的意义11

1.1.3 国内外研究的现状11

1.2 开发环境22

1.2.1 开发环境的选择22

1.2.2 开发环境的介绍22

1.2.3 OpenGL介绍33

1.2.4动态LOD技术33

2 分形地形的生成44

2.1 高度图的概念44

2.2 分形44

2.2.1 地形分形的概念44

2.2.2 随机分形地形的生成55

2.3 过程生成77

3 四叉树（quad tree）算法88

3.1 基本思想88

3.2 四叉树的数据存储99

3.3 节点判断系统99

3.4 网格的生成1111

3.4.1生成网格的意义1111

3.4.2 生成网格的方法1111

3.5 网格的渲染1111

3.5.1 网格的渲染过程介绍1212

3.5.2 网格的渲染方法1212

3.6 裂缝的消除1212

3.6.1 裂缝的形成1212

3.6.2 裂缝的消除1313

4 纹理贴图1313

4.1 地形纹理贴图1414

4.1.1 地形纹理的概念1414

4.1.2 地形纹理过程生成算法1414

4.2 高度区域的纹理贴图1515

4.2.1 区域高度的概念1515

4.2.2 高度区域的算法介绍1515

4.3 区域高度以及纹理贴图的算法1515

4.3.1 分配一个管辖的高度区域1515

4.3.2 如何遍历纹理图1717

5 裁剪1818

5.1 裁剪的介绍1919

5.2 投影技术的实现1919

6 天空盒子1919

6.1 天空盒概念2020

6.2 天空盒的制作2020

7 性能测试2020

7.1 两种绘制方法比较2121

7.2 纹理贴图的比较2121

8 论文的结论和展望2222

8.1 论文结论2323

8.2 展望2323

参考文献2424

致谢2626

1 绪论

1.1 课题研究目的及意义

1.1.1 课题研究的目的

地形场景的实时绘制是目前一个热点研究的周高点问题，目前的地理信息都是通过三维来表现出来。地形中存在很多自然景物,具有复杂多样、数据大的特点。了解三维地形的概念,在深入研究了建模技术,了解地形实时绘制之后,完成了一个基于OpenGL的地形建模。

1.1.2 课题研究的意义

从地形的构造、地物数据模型和数据结构三方面进行研究,地形建模的研究是实现三维可视化地形的关键，三维地形占有着重要地位,在游戏和旅游区规划开发上有着重要的前景, 研究具有实践意义。

1.1.3 国内外研究的现状

在三维空间数据结构算法方面，杨必胜和李清泉研究出了一种按照多分辨率三维模型基础上提出一种稳健算法，龚健雅则提出了面向对象的矢量栅格集成数据模型[6]。邓念东，侯恩科提出了一种顾及维数的三维空间拓扑描述框架[7]。Klein采用一种与视点相关的TIN数据结构来表示交互中的集合信息，当视点改变时，采用Delaunav三角剖分法重构侧TIN[21]。Luebke等提出了一种基于顶点数的简化算法，它可以对任意几何模型进行简化[10]。Hoppe将他提出的渐进式网格模型也应用到地形当中，并且提供了与视点相关的支持，为了有效避免三角剖分过多给全局带来的影响，他在算法中将地形分成大小不等的若干块，在块内进行逐一的网格剖分。这在一定程度上提高了模型简化的效率[5]。

本文通过高度图来创建地形，并且对地形进行纹理贴图，然后纳入动态LOD技术，用四又树对地形进行编写，实现了三维虚拟地形的实时绘制。如图1.1所呈现的地形形式。

图1.1 本文最后制作成功的地形

1.2 开发环境

1.2.1 开发环境的选择

现有的可供地形建模的开发工具很多，开发工具对准确合理的开发出地形有着重要意义。所以根据不同的开发工具，通过对他们之间的相互比较，最后选择基于Visual C++6.0的开发平台，并且结合OpenGL进行程序的编制[4]。

1.2.2 开发环境的介绍

Visual C++6.0是美国微软公司基于面向对象的C++语言开发的工具和编译器。在图形学领域，Visual C++有着不可比拟的优势。

使用OpenGL的目的是计算机图形开发与设计人员可以不去了解具体繁琐的硬件系统，支持OpenGL语言的硬件在平台上都可以执行[15]。用户可以通过在地形中进行游走操作，初始化OpenGL函数库，设置窗口大小和渲染等等，都需要消息响应来完成。在编写地形仿真程序时，消息响应是非常重要的[14]。见图1.2。

图1.2 Visual C++的消息映射机制

1.2.3 OpenGL介绍

OpenGL(开放性图形库)是由SGI开发的高性能图形软件处理系统。是图形硬件的软件界面[13]，它可以实现图形的定点描述，将像素保存到纹理内存，像素值被送到帧缓冲器实现图形显示。

1.2.4动态LOD技术

LOD中文翻译过来是“细节层次”， LOD技术在图形学中是一个大的话题，所涉及的不光是地形这么一个领域。对于地形我们追求的有两个目标：质量和性能。这是一对互为矛盾的指标，任何一方的提升都要以对方的降低作为代价。层次细节就是通过降低多边形数量达到一个性能的提高。设计一个评估系统，用这个标准来评估我们将要划分出多个层次，模型的表示方法为级别越高的多边形越多，反之则越低。举个列子说明：采用“近大远小”原理，当在远处看地形的时候，因为我们离着地形远，所以这里的多边形就比较少，反之则大。如果把地形起伏度也用这个描述的话，那么越是陡峭的地方多边形越多越详细，平缓的地方则不需要太多的多边形来绘制。

2 分形地形的生成

2.1 高度图的概念

高度图实际上就是一个存储数据的文件，在其中存放了地形高度数据，经过程序对它的读取，形成地形。高度图的文件格式有很多，比如bmp，jpg，tga等等。

接下来介绍一下图形学中顶点的显示。显而易见，在三维坐标系中，一定需要3个数据：即分别x轴、y轴、z轴的分量。在一个区域内绘制五个点，x轴和y轴分量都是已知的，则知道5个y轴分量即可。假设现在提供一个513*513的区间（也就是有513*513个顶点），需要513*513个y轴分量，不难发现高度图的图片尺寸也是513*513。所以说高度图它就是存储了一堆y轴数据而已。高度图一般用灰阶图表示，如图2.1所示其中的灰度的不同就表示高度的不同。灰度图中越亮的地方代表越高，越暗的地方代表越低。如图2.1所示。

图2.1 左图为一张高度图（灰度值0-255），右图对应生成的地形

2.2 分形

2.2.1 地形分形的概念

“分形”这个概念在数学领域中相当复杂。下面图2.2所示，就是一张Mandelbrot集的图片。这类图片最大的特点就是它的局部跟它的整体很相似，但是他们之间的差异还是存在的。

图2.2 曼德勃罗集

结合地形建模，实际上，高低不平的山脉就表现为一种分形。放眼望去，可以看到高高矮矮的山峦参差不齐。如果使用镜头来看，即使在局部，他们都是高低不平的，所以我们要在地形中运用分形技术[11]。

2.2.2 随机分形地形的生成

这里我们采用“菱形-正方形”算法，其思想是这样的：一个大而空的代表点的二维数组阵列开始。这个阵列应该是个正方形。而且每一条边的尺寸应该是2的N次方再加1（比如33x33， 65x65， 129x129等等）。将四个角点假设成一样的值。以一个5x5组成的正方形的数组为例。在图2.3（a）中，被赋值点用黑色显示：

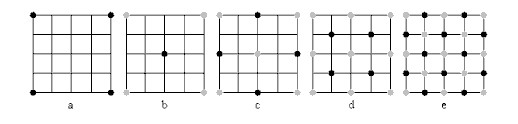
图2.3 “菱形-正方形”算法过程

此算法分为两个阶段

（1）“菱形”阶段

图b所示，把左边的两个边角点，连同那个中心点连起来，顺序是：左上点->中心点->左下点。得到了一个菱形的右半部分。其实是循环顺延到了右边，也就是右上点->中心点->右下点构成了这个菱形的左半部分。如果把半个菱形就可以算是菱形。那么这里一共有四个菱形：左上点->中心点->左下点、右上点->中心点->右下点、左上点->中心点->右上点、左下点->中心点->右下点。
（2）“正方形”阶段

通过图c可以看出，左上点->中上点->中心点->左中点构成了一个正方形，容易看出该图一共排布着4个这样的正方形。

这个阶段生成一个随机值。此时一共有四个菱形。它们全部相交一个点，就是在原正方形的中心点。所以我们要分别计算这四个菱形的中心点。对每一个菱形，求它的四个边角值的平均值，再加上那个随机值，就是各自中心点的值[16]。如图c所示，用黑色来表示新产生的点，灰色表示已经存在的点。

通过两个阶段，可以总结出来正方形和菱形的个数各是满足公式2^(I*2)的，其中I代表有几个正方形，所以可以解释为只有1个正方形；I=1时（第一次迭代），出现4个正方形；I=2时（第二次迭代），16个正方形；I=3时（第三次迭代），64个正方形。

现在让我们来了解一下粗糙度常数H，随机值取值范围每次乘的数是2^(-H) 。如果定这个常数为1，那么随机值取值范围每次都乘1/2，即第一次在[0,1]内取一个随机值，第二次在[0,0.5]内取，第三次在[0，0.25]内取。H是通过控制2^(-H) 来间接控制随机值取值范围的。

把图c得到的点用线连起来，就会得到线框图的变化过程如下图2.4：

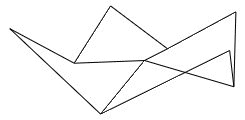
图2.4 图c随机生成的线框图

再次以“菱形”阶段开始。首先，我们这次有了4个正方形，计算这4个正方形的中心点。这次随机值的取值区间要被缩减。我们设置的H值为1的话，开始的取值范围为(-1.0 ，1.0），经过缩减得取值范围为(-0.5，0.5)。如图d所示，我们用黑色点表示计算出来的正方形的中心点。

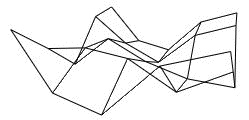
到了图数组中的25个点已经全部生成。就会得到线框图的变化过程如下图2.5：

图 2.5 图e随机生成的线框图

2.3 过程生成

过程生成是一种依靠程序，按某种算法动态生成数据的一种技术。这样看来，我们就可以把高度图，分形，过程生成三个概念联系起来。绘制出地形需要的高度图数据[9]。如果我们用这种方法，不仅可以展现出逼真的地形地貌，而且可以省去手工环节，减轻开发人员的负担。但是缺点就是要绘制的东西必须符合“分形”特征，其次，程序员无法干涉会生成什么，所有的地形都是随机生成。

3 四叉树（quad tree）算法

3.1 基本思想

通过了解了分形创建地形之后，我们再用四叉树来构建地形，运用四叉树算法我们为了便于理解，地形规定为（2n+1）×（2n+1），而且要均匀的采样。

第一次分割成四个正方形，淘汰没有目标节点的正方形，只对有目标节点的正方形再分割，随着分割的不断变大，所得到地形的分辨率变高。如图3.1展示了了分割的过程。

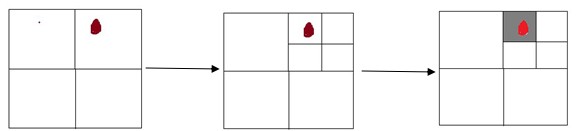
图3.1 分割过程示意图

如图3.2所示，四叉树其中每个节点中都存储着信息，规定为红色位置的为中心点，4个边点，四个角点。共9个点。

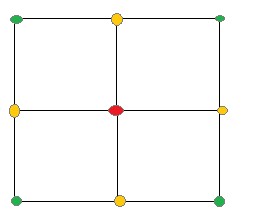
图3.2 一个节点记录的信息，包括中点，角点，边点

采用四叉树的概念来表示多分辨率的地形有很多优点，这种方法很容易的就可以在分割初期去掉不需要的节点，去掉节点之后仍需考虑节点是不是能再分割，为此还要建立一个判断条件，确定节点何时被丢弃，当节点不在视线范围内的时候就直接丢弃，而且当一个节点不能再分割的时候，被送入API渲染。

3.2 四叉树的数据存储

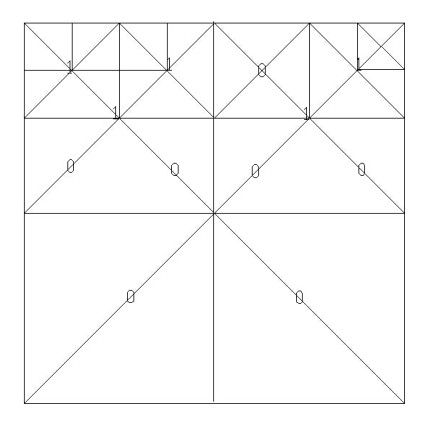
四叉树地形数据是以二维数组的方式存储在高度图中。高度图中采用顺序结构，把数据放到二维数组中，通过四叉树的节点信息可以直接通过索引被读取，四叉树本身还要建立一个标志性数组，通过这个数组来指示四叉树各个节点的状态，如图3.3所示，标记1的代表节点可以再分割，标记？表示没有被访问过，标记0的则不需要再分割。为了算法的简单易懂，本文只拿（2n+1）×（2n+1）的地形数组来解释算法。对于不满足的地形，把它们分割成符合的要求，再按照方法进行分割。

? ？？？？？？？？

? 1 ？ 1 ？ 0 ？ 1 ？

? ？ 1 ？？？ 1 ？？

? 0 ？ 0 ？ 0 ？ 0 ？

? ？？？ 1 ？？？？

? ？？？？？？？？

? ？ 0 ？？？ 0 ？？

? ？？？？？？？？

图3.3 （9×9）标记数组，分别标记的可分割，不可分割，没有访问到的节点

3.3 节点判断系统

节点判断系统可以大致由两个因素决定：

（1）与人看地形的视点有关

当距离人眼越近的话这个地方细节就会越多，反之则越少。所谓视点是由人眼到节点的距离和节点的大小决定的[3]。结合图3.4得到如下的公式：

L/d<C（C为可以调节的因子）（1）

其中L为节点的中点到人眼睛的距离，d为节点边的大小，如果满足上面公式，节点则要继续的分割。C越大，地形细节就越多。反之则少。

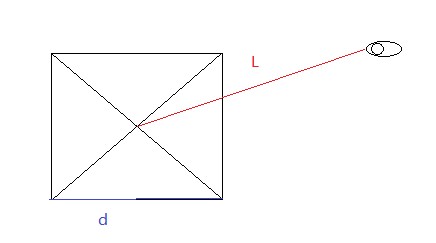
图3.4 视点：眼睛到节点的距离

（2）与地形本身的粗糙度有关

地形高低不平的区域要求有较高的细节层次，平坦的地方不要求有过多的细节。

图3.5 表示粗糙度信息

图3.5左图所示引起误差的点一共有五个，分别是四个边点和一个中点，这几个点所表示的数值越大证明越是粗糙，如图3.5右的四个子节点，我们取这九个点中的最大的一个除以节点的大小作为这个节点粗糙度的判断值，即 r = Max(dh0,⋯dh8)/d，可以看出，粗糙度的计算方法也是一个递归的过程，然而我们需要事先把粗糙度评价值计算出来，让它在运行的时候不再进行额外的计算。再存储二维数组中[1]。我们得到第二个评价公式：

1/r<C2（C2 仍然为粗糙度调节因子）（2）

C2可以理解为可调节的粗糙度因子，数值越大，细节越高。

综合（1）和（2）中得到的公式，得到最终节点判断公式：

f=L/d×r×C×C2<1 （3）

当公式（3）中f<1时，节点会被继续分割。我们来调节C、C2的数值，可以调节粗糙度。

3.4 网格的生成

3.4.1生成网格的意义

在我们渲染网格之前，最主要的一点就是更新四叉树，让它生成符合我们规定的四叉树，相邻节点间最多不能超过一个层次，否则会造成在两个不同层次的

节点拼接的地方产生裂缝，生成合法的网格有利于渲染工作。

3.4.2 生成网格的方法

遍历四叉树我们按照广度优先方法。把同一层次的所产生的节点在同一次生成，这样我们只需要遍历一次就可以。处理完当前层次队列以后，就可以进入下一个层次的节点处理。分辨率达到最大和不能分割的节点直接渲染。这样做的好处是每检查一个节点的时候，下一节点就早已经产生。通过检查看它们是否存在，若它们都存在，则继续分割这个节点，同时，在第一遍遍历四叉树的时候有信息让我们绘制三角型扇，根据下一节的方法，渲染一个节点的时候，我们只需要检查分辨率比该节点小的节点。而这些节点在上一层已经都生成。

3.5 网格的渲染

3.5.1 网格的渲染过程介绍

通过一个递归的过程来实现对地形网格的渲染。当遍历四叉树时，当遍历到四叉树的叶子时，当一个节点不再被分割时，就可以把节点绘制出。

3.5.2 网格的渲染方法

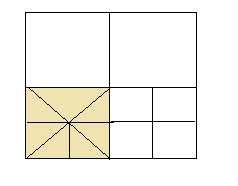
本文通过应用三角形扇（Triangle Fan）的方式来绘制，其原理就是中心点和围绕着这个点的点形成一个三角扇区。如图中棕色区域是渲染的部分。如图4.6所示，四个角点会被用到三角形扇组成中，边点则要检查与其相邻的节点，因为我们知道边点是用来共享的，如果相应的邻接节点没有被激活的话，我们就可以跳过这个边点，如图3.6中的0三角扇，不渲染。

图3.6 节点当前被渲染区域

3.6 裂缝的消除

3.6.1 裂缝的形成

生成网格的时候，如果两个节点的分辨率以及它们的层次大于1时，会产裂缝，如图3.7所示，黑点部分为裂缝点，消除这种裂缝的方法有两种，可以在裂缝产生的地方增加一条边或者去掉一条边，相对来说，去掉一条边方法更加的复杂，因为拼接处的节点的分辨率可以相差任意大，所以本文采用增加一条边的方法，它要求拼接处的两个节点的层次差距最多不超过1[2]。

图3.7 裂缝的产生过程

3.6.2 裂缝的消除

构建限制四叉树，通过图3.8所示通过增加一条边来消除裂缝，限定相邻四叉树节点之间的绘制精度等级最多不能超过1层，通过相邻地形节点块的绘制等级，在相邻块的节点处增加面片来解决消除裂缝。

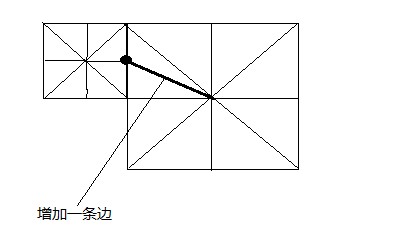
图4.8 裂缝的消除

图3.8 裂缝的消除

4 纹理贴图

4.1 地形纹理贴图

4.1.1 地形纹理的概念

使用纹理贴图可以提高变换视角看物真实性。本质上它就是贴在多边形上的一张普通纹理[20]。通过贴图可以使上一章介绍的高度图变得真实，有色彩，让它看上去像一个真的地形，场景变得逼真。由于地形是动态生成的，事先开发人员并不清楚会生成什么样的多边形，连多边形都无法指定，纹理映射又不能确定从哪里开始，用动态方法最方便，也就是用过程生成技术生成的。

图4.1 一张纹理贴图

4.1.2 地形纹理过程生成算法

首先，笼统介绍一下该算法的概念：为已经动态生成的高度图“配送”一幅恰当的纹理图。这幅纹理图应该是动态生成，应该设计自己想要的地形进行纹理贴图，达到真实的效果。

在进行纹理贴图时候，就会遇到一个问题，那就是高度。然后根据高度不同来计算出它应该具有的像素值。也就是说每一个像素都对应着高度图里面的一个高度值，我们按顺序去读取高度图中的像素值。所以要生成纹理，需要一张高度图和多张纹理图，根据算法和高度图数据来把它们结合在一块，得到的产物就是纹理图。假设我们有四张纹理图和一张高度图，根据算法来实现对其的调和[19]。具体过程通过图3.2可以加深理解。

++ + +=

图4.2 纹理生成过程

4.2 高度区域的纹理贴图

4.2.1 区域高度的概念

在地形中，我们看到的都是参差不齐，高矮不一的画面，在纹理贴图时，要为我们现有的多张纹理（根据地形高低制作出来的）进行高度分配，使画面个更加逼真。

4.2.2 高度区域的算法介绍

从上一小节写到了根据高度图来纹理贴图，其中提到的算法重点部分是为每一张纹理图分配一个自己所管辖的高度区域。

4.3 区域高度以及纹理贴图的算法

4.3.1 分配一个管辖的高度区域

假设图形编号为“黄土”--01，“雪地”--02，“草地”--03，“岩石”--04 。从前到后所对应的管辖高度区域越来越高。图3.4形象的表现出来了这一效果。所以要改进设计，达到重合的效果。设计要让每一个纹理图的管辖高度与和它相邻的纹理图的管辖高度进行部分区域的重合，重合部分两个区域共同影响，计算出一个混合它们的颜色值。

为了实现高度区域的划分，需要定义三个边界点：高点、适中点、低点，其中规定适中点高度最高。如图4.3所示，边界点设置。

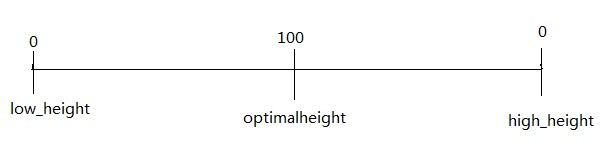
图4.3 每个管辖区域的三个边界点

对“管辖区域”这个结构做了细致的规定之后，现在关键的问题就是怎么实现平滑过渡：每个管辖区域目前有了两个区间，重合的方法就是把低一级管辖区域的optimal - high区间与相邻高一级管辖区域的low - optimal区间重合。如此一层搭一层，就像搭楼梯一样。图3.5展示了明确的意思。

图4.4 没有过度的纹理贴图

图4.5 重合之后，一层搭一层

图4.4和4.5可以看出纹理图的管辖区域：纹理01的管辖高度为0 — 60，其中，low为0 ，optimal为30，high为60；纹理02的管辖高度为30 — 90，其中，low为30，optimal为60，high为90；纹理03的管辖高度为60 — 120，其中，low为60，optimal为90，high为120；纹理04的管线高度为90 — 150，其中，low为90，optimal为120，high为150。

这个例子中，是人为规定的，但是并不准确，不知道地形的高度区域。所以我们要设计一个算法来实现区域高度。具体方法为筛选出高度图中最大的高度值，假设为max_height，然后就知道整体的跨度为0 — max_height，整体的长度就为max_height。四张图和重合的部分可以分成5各部分，除以5，得到的值就是管辖区域中的、每个区间的长度。注意，是管辖区域中的单位区间的长度，不是管辖区域本身的长度。这个例子中得到的值就是30。有了它，就可以算出具体该为每个纹理分配多大的管辖区域长度了，不仅如此，还同时可以算出其内部low、optimal、high的值。

4.3.2 如何遍历纹理图

若高度图为5x5，9x9 ，17x17，.... 513x513 。纹理图则可以为4x4，8x8，16x16，.... 512x512。这是由硬件决定的。高度图和纹理图的尺寸规律：它们相似但却不同。

高度图尺寸和纹理图尺寸匹配。如果说高度图的边长为2^N+1，纹理图则为2^N 。比如，高度图尺寸是513x513，那么要求纹理图尺寸是512x512。这样就达到最佳匹配。这并不是最优化的设计，暂且先拿这个模型讨论，之后再做优化。现在可以得出结论，一旦指定了高度图的尺寸，纹理图的尺寸也就指定了[18]。假设纹理图尺寸就是512x512。我们开辟一个对应的内存空间，用来装载计算出来的纹理像素了。

还要注意一下制作好的那几张纹理图。对它们的尺寸没有什么特殊的要求，因为它们并不会被送到渲染API中；它们没有必要和生产的纹理图一样大，当需要采集的像素位置超出它们的实际位置时，用一个余除的手法就能让它到正确的位置上。如图4.6所示。

0 255 256(=0)

图4.6 遍历到（0，256）点的时候，也就回到了（0，0）点。
这个简单的手法就是“余除”。

采用嵌套方式，来索引纹理图：索引它们的每一行，然后在索引每一行的每一个像素，开始时候要找到高度图所在位置，直接从高度图中读取这个点，然后从纹理图中找到这个点对应的像素。若所提供的纹理图和需要的尺寸不匹配，我们采用方法是之前提到的“余除”方法，通过一个小小的转换设计，就不用担心在取原纹理图时超出范围。

通过上面介绍的算法，采用的纹理图尺寸是和高度图尺寸非常匹配的（只差一行和一列的大小）。其实，采用的纹理图尺寸和高度图可以没有什么关联，只要满足计算机要求基本的2^N边长即可。换句话说，可以任意决定生成的纹理图大小。这就是优化方案。相比之下，上面的方法不仅非常简单，而且纹理图必须和高度图尺寸绑定，假如高度图的尺寸很大，纹理图也要尺寸很大，然而优化方案可以令纹理图尺寸大大减小，这样处理巨大地形时，纹理图就会节省大量的CPU运行空间，把内存的空余出来，提高CPU的工作效率。这种优化方案就是巧妙运用了“比例”的思想。对于一张并不匹配的纹理图和高度图，当纹理图遍历到某一个像素中时，根据该像素在本纹理图中的位置，找到高度图中等比例的位置的像素，然后读取它的高度值。

5 裁剪

5.1 裁剪的介绍

当我们把地形以及所有的场景都建立完毕后，我们不难发现一个问题，其实我们的电脑看上去只是一个平面，所以本章重点研究的是怎么将我们的3D模型转换到成2D，并且在这个2D平面中展现出3D效果。简单的说投影就是将一个实物（3D）体投影到电脑屏幕（2D）的过程，也就是到最后我们看到的显示器上的画面。

5.2 投影技术的实现

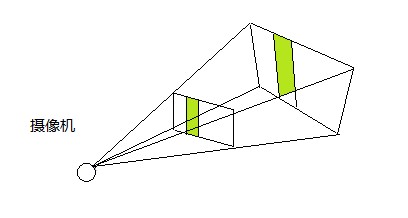
本文采用透视投影，经过投影矩阵裁剪后的坐标，比如定义一个摄像机，也就是视觉坐标，这个摄像机看到的范围是有限的，有一个夹角和一个近距离和远距离。夹角外的看不到，设置一个近距离裁剪，就是太近的也当做看不见，太远的也看不见。也就是将上述的视觉坐标定义了一个裁剪体，在这个范围内的才渲染，同时将这个视觉坐标这些3D的顶点投影到这个视景体中，也就是最后2D的画面了。如图6.1。

图 6.1 摄像机代表人的视角

6 天空盒子

6.1 天空盒概念

为了中模拟天空，天空盒制作是必要的。一般天空的构造可以使用天空盒。天空盒子可以用正方体来绘制，然后再贴图。然后这个四方体包裹着地形，这样就为地形加入了天空，做到了场景的进一步逼真。

6.2 天空盒的制作

文采用一个正方体贴图的方法来制作天空盒子，也就是把纹理映射到立方体的六个面，首先我们要准备纹理图，如图5.1，所采用的图片来制作天空盒，因为程序中加载的是tga图片文件，所以先通过Photoshop把图片格式改过来，然后把图片转换成纹理图。再将纹理正确贴到四边形上，必须将纹理的右上角映射到四边形的右上角，纹理的左上角映射到四边形的左上角，纹理的右下角映射到四边形的右下角，纹理的左下角映射到四边形的左下角。如果映射错误的话，图像显示时可能上下颠倒，侧向一边或者什么都不是。以此方式制作的天空盒子如图6.1右图所示。

6.1 左图为天空盒子制作的素材，右图为制作出来的盒子

7 性能测试

7.1 两种绘制方法比较

我们分别采用两种方法来绘制地形，分别是分形地形和四叉树地形，其中分形地形是通过正三角形来绘制地形，而四叉树则是通过细节层次来绘制，两种绘制出来的地形网格如图7.1所示。左边为分形地形产生的网格，右图为四叉树产生的网格。当我们采用四叉树绘制地形的时候可以，其中绘制效率可以提高很多，分形地形必须把整个地形所需的三角形全部绘制出来，然而四叉树绘制的时候和视点有关系，在视点内的进行绘制，不在视点内，直接忽略，这样会大大节省空间。

图7.1 两种方法产生的地形网格

7.2 纹理贴图的比较

在进行纹理贴图的时候，我们可以看到分形地形中贴完纹理之后，当我们通过键盘在其中漫游的时候，它就像一个静态的死物一样在屏幕中呈现出来，不会随着视点的改变而改变，然而四叉树构建的地形贴完纹理之后，随着在其中的漫游，它的细节层次也展现出来。我们可以看到当我们移动到某个点，随着距离的减小，地形会不断的变化，慢慢的变得非常详细。反之，我们离着地形越远，则三角形会慢慢的减少，这也能说明当我们离地形很远时，只是用了很少的三角形来绘制。这样大大提高了绘制效率。图7.2展示了这一过程。

图7.2 四叉树的网格随着远近的不同，详细程度也不同

8 论文的结论和展望

8.1 论文结论

介绍了高度图的概念，地形的数据都是存储在高度图里面，通过对高度图的数据读取，生成地形，但是这种方法要事先去规定高度图，所以本文又引进了一种方法，分形生成地形，其中采用“菱形-正方形”算法，其算法主要表现为一种随机生成地形形态。主要是一个大而空的代表点的二维数组阵列开始。这个阵列应该是个正方形。而且每一条边的尺寸应该是2的N次方再加1，然后通过正方形和菱形的不断交换来生成我们需要的点，其中每一个菱形和正方形的中点都会产生一个高度值。就是地形的高度把所有高度表现出来就成了地形。
然后进行纹理贴图，从生成的高度图中得到了地形的各个区域的高度。所以根据高度可以进行贴图，这其中最难理解的就是区域高度的划分，我们通过为四张纹理图根据不同的高度进行纹理贴图，来实现了每个高度区域有一张纹理图，对“管辖区域”这个结构做了细致的规定之后，实现平滑过渡：每个管辖区域目前有了两个区间，重合的方法就是把低一级管辖区域的optimal - high区间与相邻高一级管辖区域的low - optimal区间重合。其中重合部分，通过像素所对应的颜色值来混合，实现平滑过度。
以上方法实现的地形模型是由许多三角形来绘制的，三角形的数量非常大，要在每一帧显示所处理的数据。这样会造成CPU的吃不消。不能更好的实现漫游。事实上，我们只是在观察地形的某一个区域，所以引进四叉树算法来编写地形，这样也使整个地形纳入了动态的LOD技术，从而也达到了更高的要去，四叉树算法主要是把地形分成具有层次细节的正方形再通过视点与节点的距离来进行层析划分，给我们的效果就是当靠近地形时候，就会产生更多的节点。当们视野远离地形时就会减少节点数量。对编写过程中产生的裂缝进行消除，得出结论，相邻节点间的层次差别不能大于1。最后对地形进行渲染，渲染过程中，是通过三角扇来渲染的，节点中角点必定在三角扇中，而边点是否渲染，则要看与其相连的节点是否被激活，如果没有激活，就不渲染这个边点所在的三角扇。
通过对两种方法的对比发现，四叉树构建地形要比分形生成地形的效率要提高一倍。

8.2 展望

通过对本论文运用到方法进行总结，发现此课题还有很多值得研究的方向：

在多分辨率领域研究现有的算法，能否结合本文提出的算法，在地形动态管理方向研究出更高效的算法。
研究更好的数据分析方法。
结合GIS进行相关研究，寻找更优的新算法。

参考文献

[1] 柯希林,曾军.动态LOD四叉树虚拟地形绘制[J]. 测绘通报,2005,(06):10.

[2] 潘李亮,基于LOD的大规模真实感室外场景实时渲染技术的初步研究[J].西安工业大学软件学院,2009,(04):112-115.

[3] 王宏武,董士海.一个与视点相关的动态多分辨率地形模型[J]. 计算机辅助设计与图形学学报,2000,(08):05-06.

[4] 勒海亮,高井祥,康建荣.基于VC和OpenGL的地形三维可视化[J].微计算机应用,2006,(5):577-581.

[5] Hugues Hoppe.Smooth View-Dependent Level-of-Detail Control and its application to Terrain Rendering[C].IEEE Visualization 1998,October 1998:35-42.

[6] 杨必胜,李清泉,龚健雅.一种快速生成和传输多分辨率三维模型的稳健算法[J],科学通报 ,2006,51(13):1589-1594.

[7] 邓念东,侯恩科,霍正东.应用SURPAC实现矿床三维可视化地质模型动态更新[J].陕西煤炭,2006,(03):7-9.

[8] 齐安文,吴立新.基于类三棱柱的三维地质模拟与拓扑研究[J].矿山测量,2003,(3):65-66.

[9] 魏海涛. 计算机图形学[M]. 北京:电子工业出版社,2006(1):285-288.

[10] David Luebke,Carl Erikson.View-Dependent Simplification of Arbitrary Polygonal EnVironme-nts[C].In:SIGGRAPH’97 Proceedings,1997.

[11] 白燕武,史惠康.OpenGL三维图形库编程指南[M].北京:机械工业出版社,1998:208-230.

[12] 张严辞,刘学慧,吴恩华.基于图像的实时漫游[J].计算机辅助设计与图形学学报,2008(4):8-10.

[13] 向世明. Visual C++数字图像与图形处理[M]. 北京: 电子工业出版社,2002:168.

[14] 潇湘工作室.OpenGL超级宝典[M].北京:人民邮电出版社,2001.

[15] 吕凤翥.C++语言程序设计[M].北京:电子工业出版社,2002(2):4-16.

[16] 曹晓光.随机中点位移算法的改进[J].中国图象图形学报,1997,2(4):235-238.

[17]丁玮,齐东旭.分形生成的递归细化算法[J].中国图象图形学报,1998,3(2):123-127.

[18] 黄超超,凌永顺,吕相银.地形纹理映射方法研究[J].计算机仿真,2005,21(1):209-212.

[19] 孔令德.计算机图形学基础教程(Visual C++版)[M].北京:清华大学出版社,2013,3(2):310-324.

[20] 冯磊,宋现锋,石泰来. 3DGIS中复合地形纹理生成与应用[J].地理与地理信息科学,2009,25(2):15-18.

[21] Reinhard Klein,Tobias Huttner. Simple Came-radependent approximation of terrain surfaces for fast visualization and animation[C].In:RYangel editor,visualization 96 ACM,1996-11.

致谢

通过几个月的努力，我完成了毕业设计以及论文，在这个时候，我首先要感谢我的指导老师孔令德教授，感谢孔老师这几个月来对我细心指导，在这段时间里，老师敏捷的思维和独有的个性给了我很大的启发，让我学会了在以后的社会生活中怎样去把自己的优点无保留的发挥出来。在这期间我也了解到了孔老师的知识渊博和严谨的教学态度，早已具备了站在知识制高点的能力。通过和孔老师的相处，发现孔老师是一个对生活积极乐观、充满自信且淡泊名利的人。这对我以后的生活会有很大的影响。

在我即将毕业之际，我要饱含深情的感谢我的母校，感谢太原工业学院以及计算机系的领导和老师，四年里，在老师的悉心教导下，我已成为一个具有知识的大学生，并且我也一直锻炼自己，不怕困难，勇敢向前，慢慢的我也走向了成熟，到了现在，我已经做好了一切准备准备服务于社会，请母校放心。

我还要真挚感谢我的家人、我的女友、和我的朋友们，你们多年来对我的关心、照顾、理解和支持让我感觉到我人生的很美好，和你们在一起的成长经历是我人生的宝贵财富，是你们让我有动力去完成学业，完成人生需要的每一步。有你们，无所畏惧！

感谢所有帮助过我、关心过我的人！