目录

前言

一、树的概念及结构

1 树的概念

2 树的相关概念

二、二叉树的概念及结构

1.二叉树的概念

2. 特殊的二叉树

3. 二叉树的性质

4.二叉树的存储结构

三、二叉树的顺序结构及实现

1.堆的性质

2.堆的插入

3.堆的实现

堆的结构体

HeapInit 初始化

HeapPush 插入

HeapPop 删除

HeapTop 堆顶元素

HeapEmpty 判空函数

HeapSize 数据个数

4.堆的代码

Heap.h

Heap.c

Test.c

前言

我们之前所学的结构属于线性结构，而树是一种非线性的数据结构，它是由n（n>=0）个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的。

一、树的概念及结构

1 树的概念

树是一种非线性的数据结构，它是由n（n>=0）个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的。

有一个特殊的结点，称为根结点，根节点没有前驱结点
除根节点外，其余结点被分成M(M>0)个互不相交的集合T1、T2、……、Tm，其中每一个集合Ti(1<= i <= m)又是一棵结构与树类似的子树。每棵子树的根结点有且只有一个前驱，可以有0个或多个后继。因此，树是递归定义的。

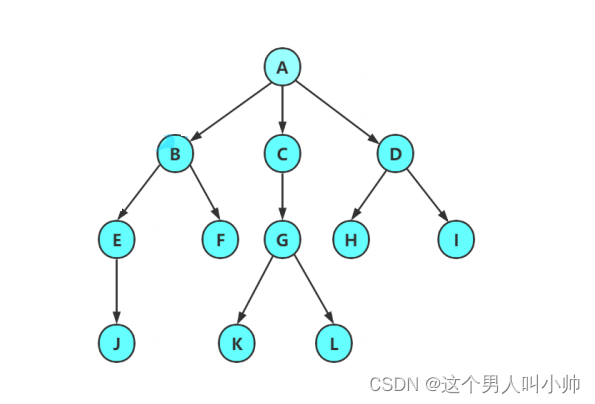
注意：树形结构中，子树之间不能有交集，否则就不是树形结构

2 树的相关概念

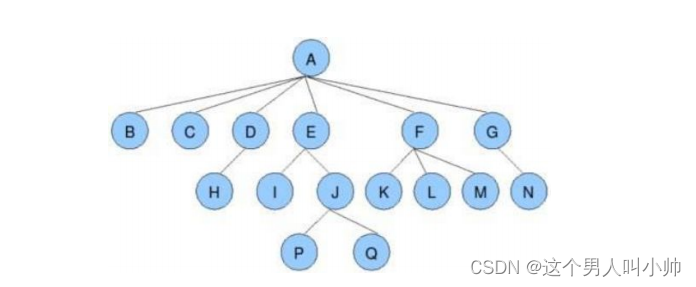
节点的度：一个节点含有的子树的个数称为该节点的度；如上图：A的为6
叶节点或终端节点：度为0的节点称为叶节点；如上图：B、C、H、I...等节点为叶节点
非终端节点或分支节点：度不为0的节点；如上图：D、E、F、G...等节点为分支节点
双亲节点或父节点：若一个节点含有子节点，则这个节点称为其子节点的父节点；如上图：A是B的父节点
孩子节点或子节点：一个节点含有的子树的根节点称为该节点的子节点；如上图：B是A的孩子节点
兄弟节点：具有相同父节点的节点互称为兄弟节点；如上图：B、C是兄弟节点
树的度：一棵树中，最大的节点的度称为树的度；如上图：树的度为6
节点的层次：从根开始定义起，根为第1层，根的子节点为第2层，以此类推；
树的高度或深度：树中节点的最大层次；如上图：树的高度为4
堂兄弟节点：双亲在同一层的节点互为堂兄弟；如上图：H、I互为兄弟节点
节点的祖先：从根到该节点所经分支上的所有节点；如上图：A是所有节点的祖先
子孙：以某节点为根的子树中任一节点都称为该节点的子孙。如上图：所有节点都是A的子孙
森林：由m（m>0）棵互不相交的树的集合称为森林；

树的一种结构体储存形式：左孩子右兄弟

typedef int DataType;
struct TreeNode
{
    struct TreeNode* pNextBrother;
    struct TreeNode* firestChild1;
    DataType data;
    
};

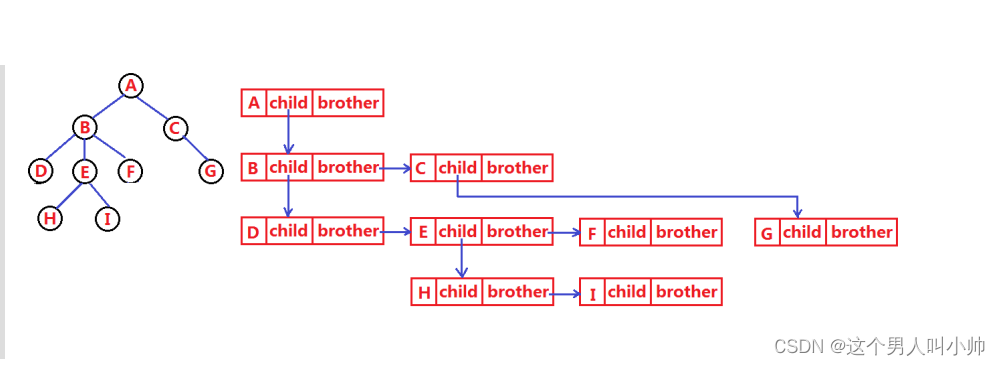
树在实际中的运用，例如树状目录结构

在数据结构中，我们基本不使用多分枝树这一结构，而使用特殊的树——二叉树

二、二叉树的概念及结构

1.二叉树的概念

一棵二叉树是结点的一个有限集合，该集合:

1. 或者为空

2. 由一个根节点加上两棵别称为左子树和右子树的二叉树组成

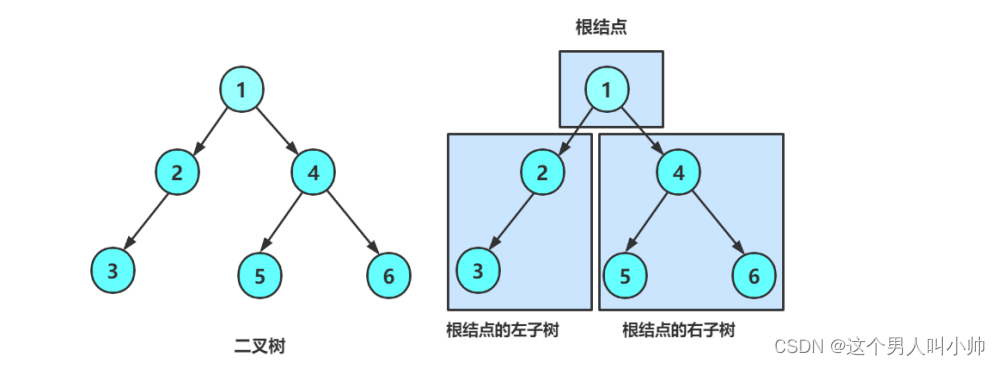
注意：

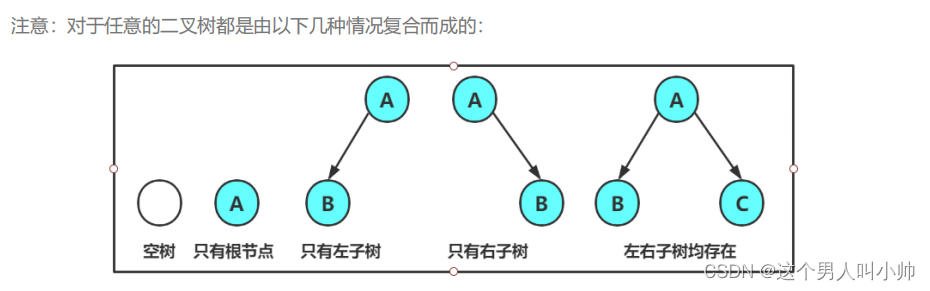
1. 二叉树不存在度大于2的结点

2. 二叉树的子树有左右之分，次序不能颠倒，因此二叉树是有序树

2. 特殊的二叉树

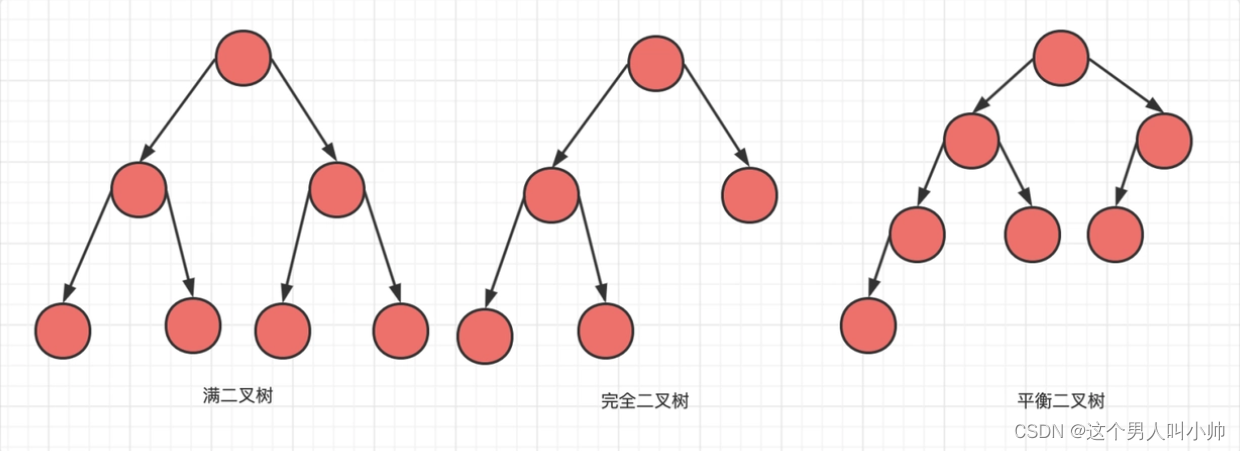
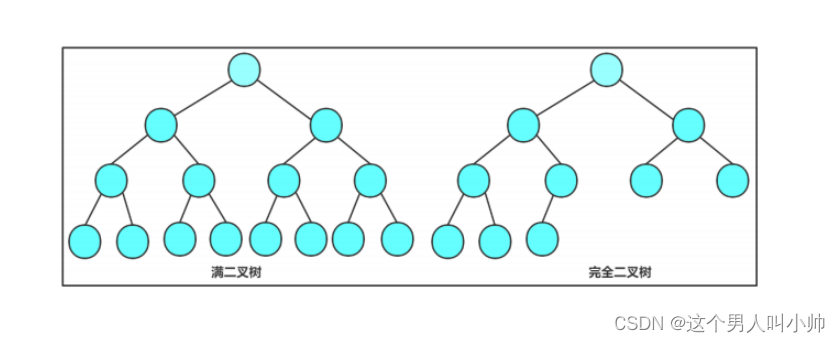
满二叉树：一个二叉树，如果每一个层的结点数都达到最大值，则这个二叉树就是满二叉树。也就是说，如果一个二叉树的层数为K，且结点总数是2^k - 1 ，则它就是满二叉树。

完全二叉树：完全二叉树是效率很高的数据结构，完全二叉树是由满二叉树而引出来的。对于深度为K的，有n个结点的二叉树，当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。要注意的是满二叉树是一种特殊的完全二叉树。

前h-1层是满的，最后一层是连续的

3. 二叉树的性质

1. 若规定根节点的层数为1，则一棵非空二叉树的第i层上最多有2^( i - 1) 个结点.

2. 若规定根节点的层数为1，则深度为h的二叉树的最大结点数是 2^h - 1

3. 对任何一棵二叉树, 如果度为0其叶结点个数为n0 , 度为2的分支结点个数为 n2,则有 n0＝ n2＋1

4. 若规定根节点的层数为1，具有n个结点的满二叉树的深度

5. 对于具有n个结点的完全二叉树，如果按照从上至下从左至右的数组顺序对所有节点从0开始编号，则对于序号为i的结点有：

若i>0，i位置节点的双亲序号：(i-1)/2；i=0，i为根节点编号，无双亲节点
若2i+1<n，左孩子序号：2i+1，2i+1>=n否则无左孩子
若2i+2<n，右孩子序号：2i+2，2i+2>=n否则无右孩子

例题1：

度为0的结点数为N0

度为1的结点数为N1

度为2的结点数为N2

2n = N0 + N1 + N2

2n = N0 + N1 + N0 - 1

又因为是完全二叉树，所以N1要么是0那么是1

2n = 2N0 - 1 + N1

又因为奇偶数，所以N1必为1，选A

例题2：

因为如果一个完全二叉树高度为h，则它的结点数在[2^(h-1) ，2^h -1 ]

所以是B

例题3：

767 = 2N0 -1 + N1

所以N1为0，N0为384，选B

4.二叉树的存储结构

二叉树一般可以使用两种结构储存，顺序结构、链式结构

4.1 顺序结构

顺序结构存储时使用数组来存储，适合表示满二叉树和完全二叉树，因为完全二叉树不会有空间的浪费。顺序结构在物理逻辑上时一个数组，在逻辑结构上是一棵二叉树。

规定根节点在数组内下标是0，根据满二叉树性质，我们可以推导出父子节点在数组中的下标关系

parent = （child - 1）/ 2
leftchild = parent *2 +1
rightchild = parent*2 + 2

4.2 链式结构

如果是非完全二叉树，那么顺序存储就不适合了，因为会造成空间的浪费，空间利用率不高，所以数组存储表示二叉树只适合完全二叉树

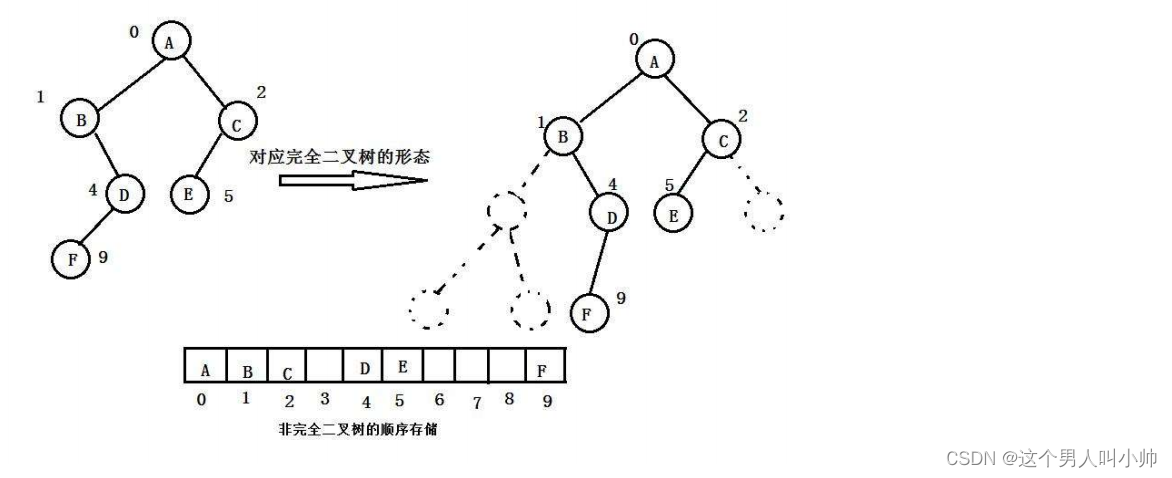
三、二叉树的顺序结构及实现

普通的二叉树是不适合用数组来存储的，因为可能会存在大量的空间浪费。而完全二叉树更适合使用顺序结构存储。现实中我们通常把堆(一种二叉树)使用顺序结构的数组来存储，需要注意的是这里的堆和操作系统虚拟进程地址空间中的堆是两回事，一个是数据结构，一个是操作系统中管理内存的一块区域分段。

注意：堆在物理逻辑上时一个数组，在逻辑结构上是一棵二叉树。

1.堆的性质

堆中某个节点的值总小于等于或大于等于其父节点的值
堆是一颗完全二叉树
所有父节点大于等于孩子的堆称为大根堆，反之所有父节点都小于等于孩子的堆称为小根堆

2.堆的插入

根据堆是大根堆或小根堆，来选择向上调整或向下调整，向堆内插入数据，应按照数组储存顺序挨个插入，在插入后，要判断其与父节点的大小关系，选择向上调整（大根堆）或向下调整（小根堆），直到满足条件为止

3.堆的实现

堆的结构体

typedef int HPDataType;
typedef struct Heap
{
	HPDataType* a;
	int size;
	int capacity;
}HP;

HeapInit 初始化

void HeapInit(HP* php)
{
	assert(php);

	php->a = (HPDataType*)malloc(sizeof(HPDataType) * 4);
	if (php->a == NULL)
	{
		perror("malloc fail");
		return;
	}

	php->size = 0;
	php->capacity = 4;
}

HeapPush 插入

插入后需要和父节点比较大小，进行向上调整或向下调整，所以单独封装一个函数实现该功能
判断要插入时，size与capacity的值是否相等，进而判断是否要扩容（在顺序表和栈中我们都学过）
最坏情况为新插入的数据最大，一直交换到根节点

void Swap(HPDataType* p1, HPDataType* p2)
{
	HPDataType x = *p1;
	*p1 = *p2;
	*p2 = x;
}

// 除了child这个位置，前面数据构成堆
void AdjustUp(HPDataType* a, int child)
{
	int parent = (child - 1) / 2;//父节点就这样算
	//while (parent >= 0) 当child = 0的时候，parent计算之后也是0，还会进入循环，这是错误的，但是又因为if条件不满足，所以break跳出循环了，这就是著名的虽然错误但是莫名其妙跑起来了

	while (child > 0)
	{
		if (a[child] > a[parent])
		{
			Swap(&a[child], &a[parent]);
			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{
			break;
		}
	}
}

void HeapPush(HP* php, HPDataType x)
{
	assert(php);

	if (php->size == php->capacity)
	{
		HPDataType* tmp = (HPDataType*)realloc(php->a, sizeof(HPDataType) * php->capacity * 2);
		if (tmp == NULL)
		{
			perror("realloc fail");
			return;
		}
		php->a = tmp;
		php->capacity *= 2;
	}

	php->a[php->size] = x;
	php->size++;

	AdjustUp(php->a, php->size - 1);//向上调整，因为size++了，所以size-1
}

HeapPop 删除

我们要考虑有意义的删除，即如果删除尾部数据，堆并没有什么实际的作用，而如果我们删除堆顶数据，那么我们可以得到第二大或第二小的数据，这在现实生活中是有意义的，因为生活中有许多排序，找到排名前k的数据，这是一个有实际需求的功能，所以，我们删除堆顶元素
要删除堆顶数据的话，不能挪动删除（将后面的数据前移），因为这样搞不仅效率低，而且搞完之后父子兄弟关系全都会乱，最优方法是，将堆顶数据与最后一个数据进行交换，再删除最后一个数据，这样既不会使父子兄弟间关系混乱，也能做到有实际意义
与会后一个数据交换后，堆的结构已经发生改变，我们要恢复堆的结构，将堆顶元素向下调整，即与它的两个孩子中最大的孩子比较大小，进而进行交换调整，最坏情况到叶子节点
在向下调整函数中，会出现数组越界风险，在循环时要加以判断


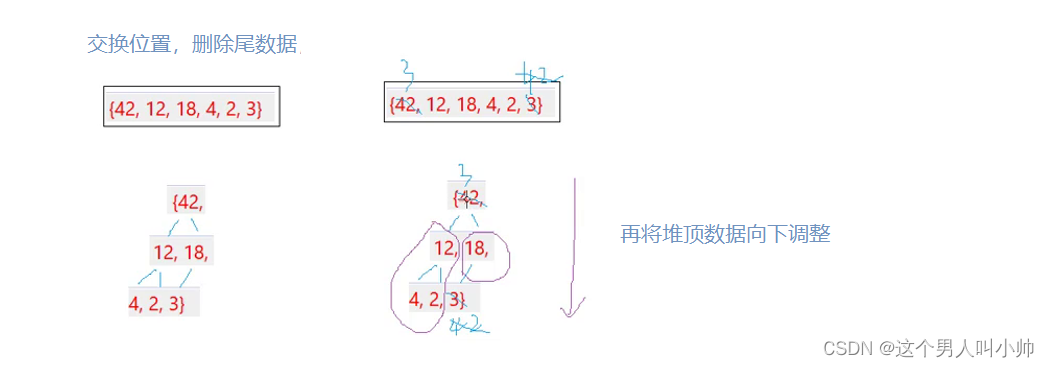
// 左右子树都是大堆/小堆
void AdjustDown(HPDataType* a, int n, int parent)
{
	int child = parent * 2 + 1;
	while (child < n)
	{
		// 选出左右孩子中大的那一个
		//这里有小问题，该点是否有右孩子，如果没有那么child+1就越界了，所以要先判断右孩子是否存在，并且还要注意逻辑判断不能写反
		if (child + 1 < n && a[child + 1] > a[child])
		{
			++child;
		}

		if (a[child] > a[parent])
		{
			Swap(&a[child], &a[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

void HeapPop(HP* php)//删除要删堆顶数据，因为删尾没有什么意义
					 //删了堆顶，那么第二大或第二小的数据就会显现出来，这对于现实top k问题都是有意义的
{
	assert(php);
	assert(!HeapEmpty(php));

	// 删除数据
	Swap(&php->a[0], &php->a[php->size - 1]);
	php->size--;//size--，减小有效范围

	AdjustDown(php->a, php->size, 0);
}

HeapTop 堆顶元素

HPDataType HeapTop(HP* php)
{
	assert(php);
	return php->a[0];
}

HeapEmpty 判空函数

bool HeapEmpty(HP* php)
{
	assert(php);
	return php->size == 0;
}

HeapSize 数据个数

int HeapSize(HP* php)
{
	assert(php);
	return php->size;
}

4.堆的代码

Heap.h

#pragma once

#include<stdio.h>
#include<assert.h>
#include<stdlib.h>
#include<stdbool.h>

// 
typedef int HPDataType;
typedef struct Heap
{
	HPDataType* a;
	int size;
	int capacity;
}HP;

void HeapInit(HP* php);
void HeapDestroy(HP* php);

void HeapPush(HP* php, HPDataType x);
void HeapPop(HP* php);
HPDataType HeapTop(HP* php);
bool HeapEmpty(HP* php);
int HeapSize(HP* php);

void AdjustUp(HPDataType* a, int child);
void AdjustDown(HPDataType* a, int n, int parent);

Heap.c

#define _CRT_SECURE_NO_WARNINGS 1
#include "Heap.h"

void HeapInit(HP* php)
{
	assert(php);

	php->a = (HPDataType*)malloc(sizeof(HPDataType) * 4);
	if (php->a == NULL)
	{
		perror("malloc fail");
		return;
	}

	php->size = 0;
	php->capacity = 4;
}

void Swap(HPDataType* p1, HPDataType* p2)
{
	HPDataType x = *p1;
	*p1 = *p2;
	*p2 = x;
}

// 除了child这个位置，前面数据构成堆
void AdjustUp(HPDataType* a, int child)
{
	int parent = (child - 1) / 2;//父节点就这样算
	//while (parent >= 0) 当child = 0的时候，parent计算之后也是0，还会进入循环，这是错误的，但是又因为if条件不满足，所以break跳出循环了，这就是著名的虽然错误但是莫名其妙跑起来了

	while (child > 0)
	{
		if (a[child] > a[parent])
		{
			Swap(&a[child], &a[parent]);
			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{
			break;
		}
	}
}

void HeapPush(HP* php, HPDataType x)
{
	assert(php);

	if (php->size == php->capacity)
	{
		HPDataType* tmp = (HPDataType*)realloc(php->a, sizeof(HPDataType) * php->capacity * 2);
		if (tmp == NULL)
		{
			perror("realloc fail");
			return;
		}
		php->a = tmp;
		php->capacity *= 2;
	}

	php->a[php->size] = x;
	php->size++;

	AdjustUp(php->a, php->size - 1);//向上调整，因为size++了，所以size-1
}

// 左右子树都是大堆/小堆
void AdjustDown(HPDataType* a, int n, int parent)
{
	int child = parent * 2 + 1;
	while (child < n)
	{
		// 选出左右孩子中大的那一个
		//这里有小问题，该点是否有右孩子，如果没有那么child+1就越界了，所以要先判断右孩子是否存在，并且还要注意逻辑判断不能写反
		if (child + 1 < n && a[child + 1] > a[child])
		{
			++child;
		}

		if (a[child] > a[parent])
		{
			Swap(&a[child], &a[parent]);
			parent = child;//先移动parent
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}
//不能挪动删除，因为这样搞不仅效率低，而且搞完之后父子兄弟关系全都会乱
void HeapPop(HP* php)//删除要删堆顶数据，因为删尾没有什么意义
					 //删了堆顶，那么第二大或第二小的数据就会显现出来，这对于现实top k问题都是有意义的
{
	assert(php);
	assert(!HeapEmpty(php));

	// 删除数据
	Swap(&php->a[0], &php->a[php->size - 1]);
	php->size--;

	AdjustDown(php->a, php->size, 0);
}

HPDataType HeapTop(HP* php)
{
	assert(php);
	return php->a[0];
}

bool HeapEmpty(HP* php)
{
	assert(php);
	return php->size == 0;
}

int HeapSize(HP* php)
{
	assert(php);
	return php->size;
}

Test.c

#define _CRT_SECURE_NO_WARNINGS 1
#include "Heap.h"

int main()
{
	HP hp;
	HeapInit(&hp);
	HeapPush(&hp, 4);
	HeapPush(&hp, 18);
	HeapPush(&hp, 42);
	HeapPush(&hp, 12);
	HeapPush(&hp, 21);
	HeapPush(&hp, 3);
	HeapPush(&hp, 5);
	HeapPush(&hp, 5);
	HeapPush(&hp, 50);
	HeapPush(&hp, 5);
	HeapPush(&hp, 5);
	HeapPush(&hp, 15);
	HeapPush(&hp, 5);
	HeapPush(&hp, 45);
	HeapPush(&hp, 5);

	int k = 0;
	scanf("%d", &k);
	while (!HeapEmpty(&hp) && k--)
	{
		printf("%d ", HeapTop(&hp));
		HeapPop(&hp);
	}
	printf("\n");

	return 0;
}