重心坐标计算

重心坐标比较简单，取最大包围合再计算点是否在三角形内就行，再根据重心坐标返回的alpha,beta,gamma三个权重值计算 uv映射和depth深度缓冲值，因为是求的重心坐标，感觉效果比插值的要好一点。

求重心坐标

           barycentric(a, b, c, p) {
                            let u = [
                                b[0] - c[0],
                                c[0] - a[0],
                                p[0] - c[0]
                            ]
                            let v = [
                                b[1] - c[1],
                                c[1] - a[1],
                                p[1] - c[1]
                            ]
                            let area = u[0] * v[1] - v[0] * u[1]
                            const alpha = (u[2] * v[0] - v[2] * u[0]) / area
                            const beta = (u[2] * v[1] - v[2] * u[1]) / area
                            const gamma = 1 - alpha - beta
                            if (Math.abs(area) < 1) return [-1, 1, 1];
                            return new Float32Array([alpha, beta, gamma])
                        }

插值计算

插值计算的话，首先需要逐行扫描填充，按y排序从左到右去填充三角形,再根据a,b,c三个顶点坐标信息来求uv插值和z插值，过程稍微麻烦一点，但性能明显好一点，
纹理不是采用的就近原则，是用的双线线插值计算,所以也耗了一点性能，加载的模型文件效果还是显示出来了,
写这些重要主要用c++，c++支持并行计算和着色.用JS写主要是为了解一些算法和渲染原理

求插值：

interpolate(a,b,t){
    return a*(1-t)+b*t;
}

这是插值计算渲染

 

 

 

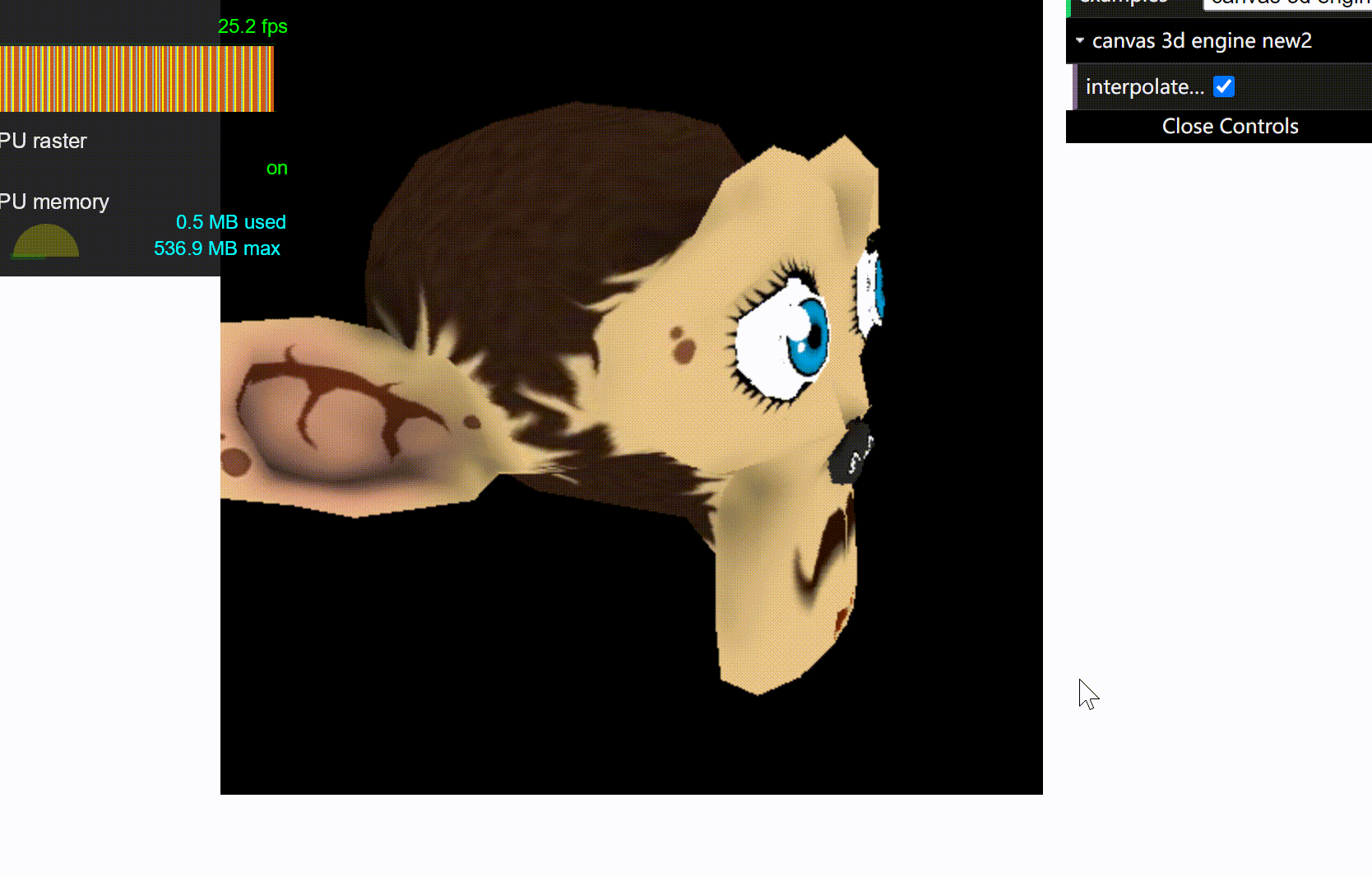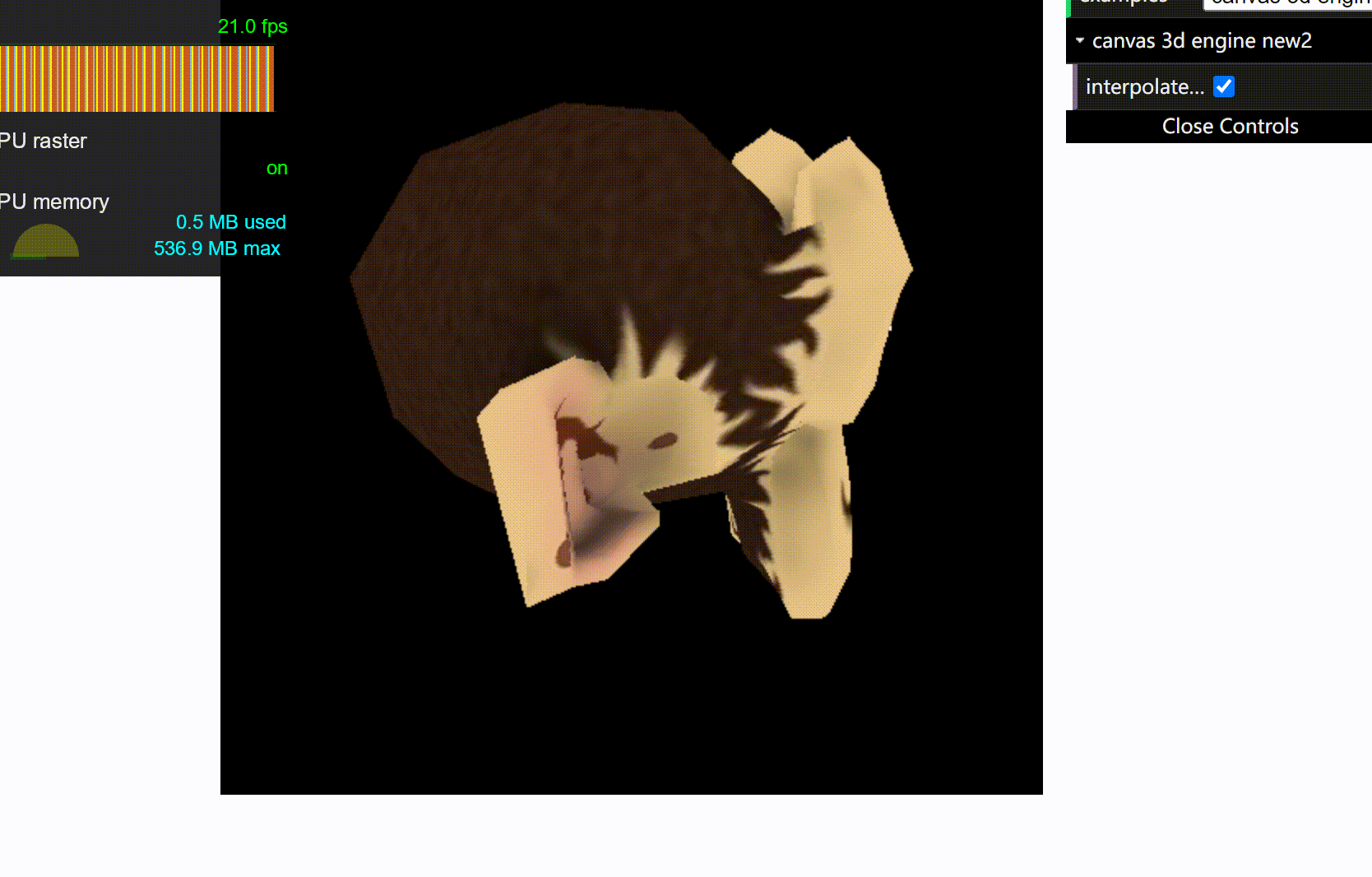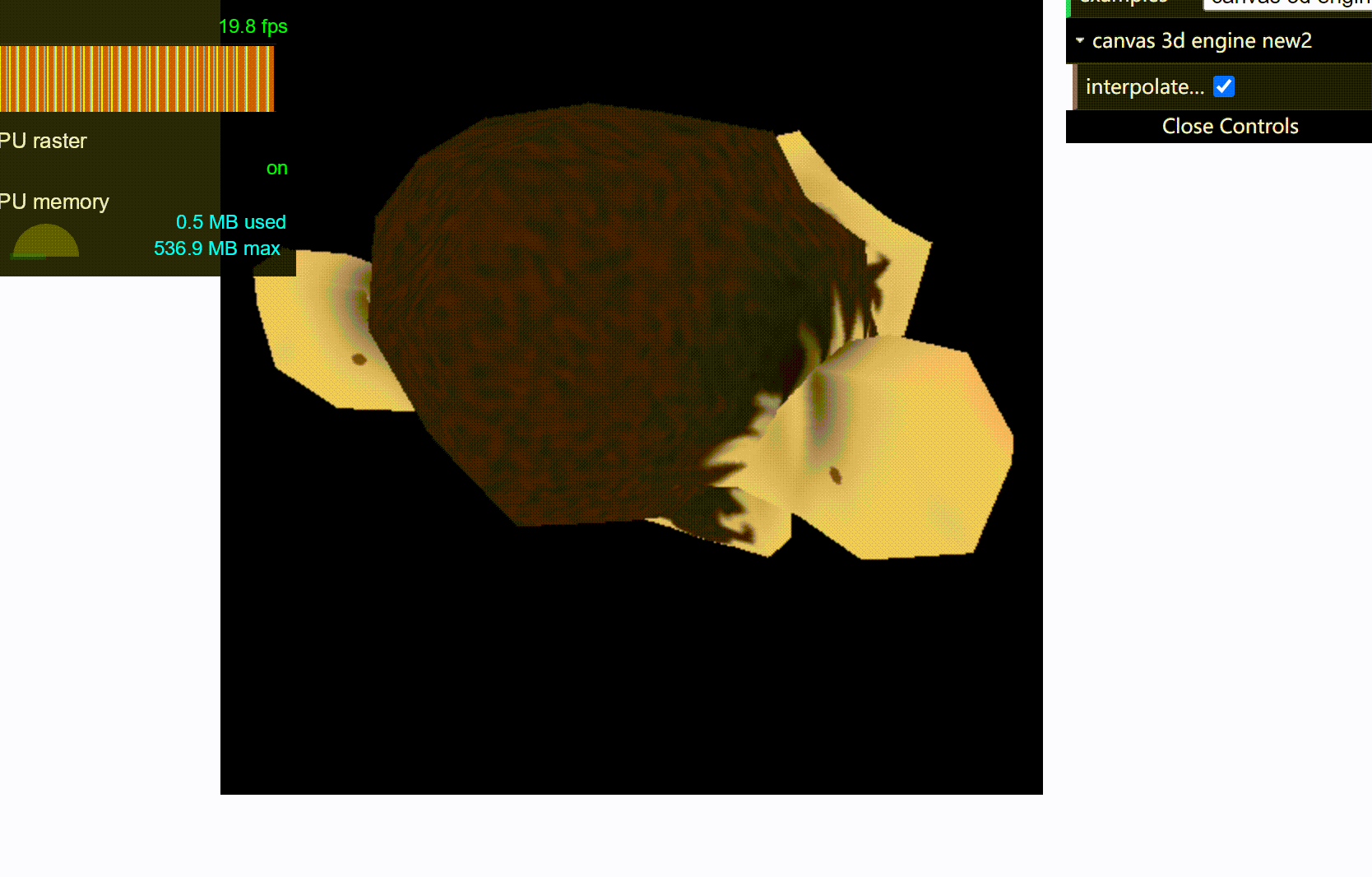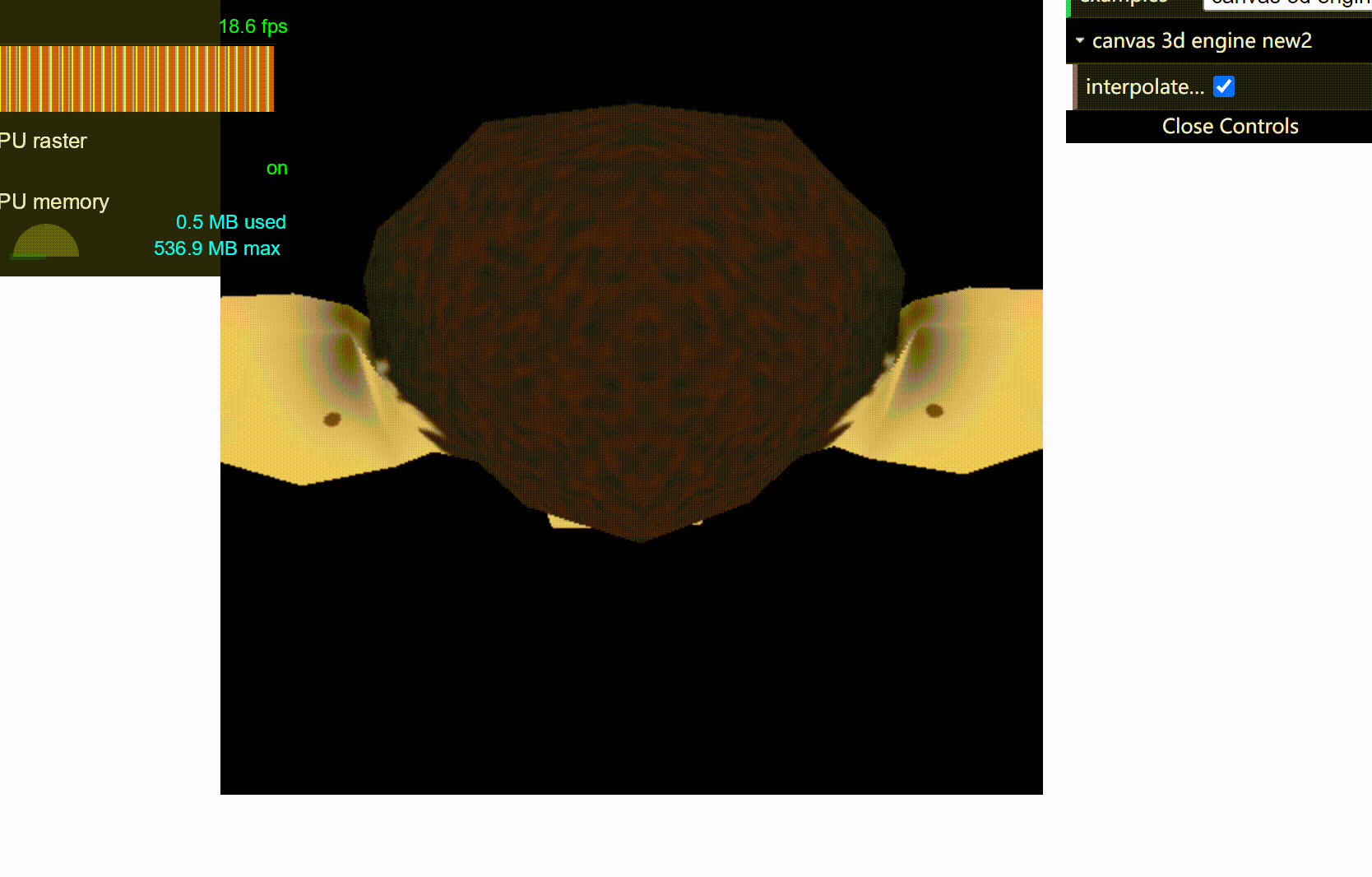
这是采用的重心坐标渲染：