1 题目来源：
牛客网：排序子序列
2 题目描述
 牛牛定义排序子序列为一个数组中一段连续的子序列,并且这段子序列是非递增或者非递减排序。牛牛有一个长度为n的整数数组A,他现在有一个任务是把数组A分为若干段排序子序列,牛牛想知道他最少可以把这个数组分为几段排序子序列.
  如样例所示,牛牛可以把数组A划分为[1,2,3]和[2,2,1]两个排序子序列,至少需要划分为2个排序子序列,所以输出2
  
3 输入/出描述
  输入：
    输入的第一行为一个正整数n(1 ≤ n ≤ 10^5)
    第二行包括n个整数A_i(1 ≤ A_i ≤ 10^9),表示数组A的每个数字。
  输出：
    输出一个整数表示牛牛可以将A最少划分为多少段排序子序列
4 示例
  输入：
  
 输出：
 
5、解题思路
  题目中定义的排序子序列需要满足以下两个条件：
    (1) 连续的
    
    (2) 非递增或者非递减排序
    
5.1 非递增非递减序列

1,2,3,4,5         //递增排列 
9,8,7,6,5         //递减排列 
1,2,3,3,4,5,8,8   //非递减排列 
9,8,7,7,6,5,5,2,1 //非递增排列

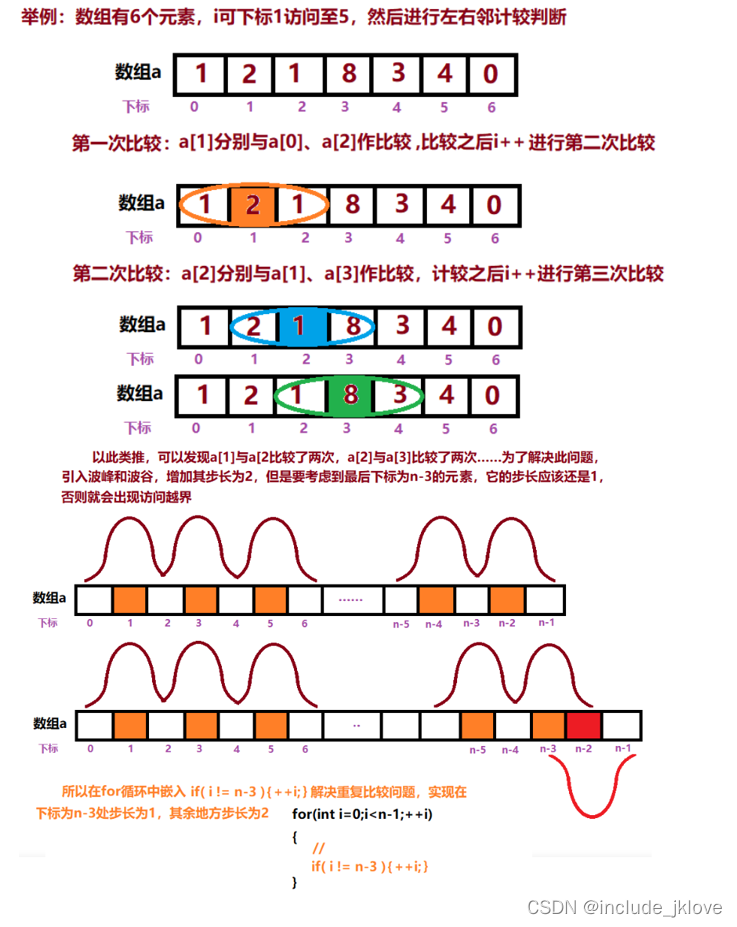
5.2 访问边界的确定
  遍历数组，拿到数组的元素a[i]后，与它的左右邻进行比较，符合非递增非递减序列，就将排序子序列的计数+1。这里需要注意以下两点的问题。

5.2.1 越界问题
5.2.2 波峰波谷问题!

6、代码展示
JAVA

public class arraydiv {
    public static void main(String[] args) {
        Scanner sc =new Scanner(System.in);
        int n=sc.nextInt();
        //创建一个数组长度为n的数组
      int[] nums =new int[n];
      //给数组赋值
        for (int i = 0; i < n; i++) {
            nums[i]=sc.nextInt();
        }
        //定义一个sum接收返回值
        //数组子数组最少为一(1s是数组本身)
        int sum=1;
        //遍历数组找到
        for (int i = 1; i < n-1; i++) {
            if (nums[i-1]<nums[i]&&nums[i]>nums[i+1]||nums[i-1]>nums[i]&&nums[i]<nums[i+1]) {
                //条件符合sum++
                sum++;
                //  //当下标未访问到n-3时，这里的i++已经比较过了，则需要跳过
                if (i!= n-3) {
                    i++;
                }
            }

        }
        System.out.println(sum);
    }
}