推断统计：研究如何利用样本数据来推断总体特征

描述统计：描述一组数据的特征

参数估计：利用样本信息估计总体特征

假设检验：利用样本信息判断对总体的假设是否成立

一.参数估计

就是对于总体指标的估计

估计：根据你拥有的信息来对现实世界进行某种判断

总体均值：真实的总体均值和预估的总体均值

样本均值：将样本中的数字相加，然后除以这些数字的总数

点估计量：总体均值的估计

1.总体均值的估计步骤

①收集样本数据

②用样本均值作为总体均值

2.总体方差的估计

方差是所有数值偏离均值的程度，样本相对于总体来说数量变少了，极端值出现在样本中的可能性就会下降。而极端值是最容易影响总体方差的因素，所以，样本方差会小于总体方差，而且样本量越少，差距越大

如果不能使用样本方差，那我们就用其他方式来估计总体方差

这个算法和样本方差的算法相似，不过除数是n-1，而不是n

这样估计得出的值要比样本方差略大，而总体方差本身就大于样本方差，所以这个公式作为总体方差的点估计量，效果更好

3.总体比例的估计

可以用样本成功的比例来作为总体成功比例的点估计量

4.样本均值的期望

①对于E(x+y) = E(x) + E(y)，假设 x 前面有一个系数A，那么E(Ax) = AE(x)

②E(x) = (x1 + x2 + ... + xn)/n

③E(x) = (μ + μ + ... + μ)/n

5.样本均值的方差

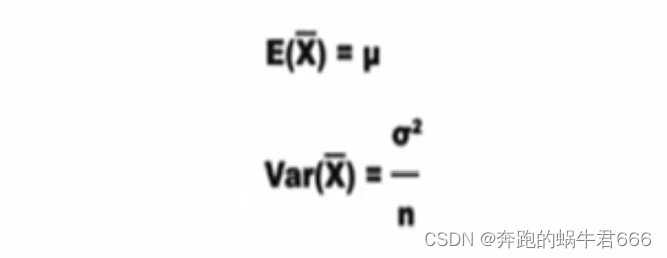
X的标准差即方差的平方根，这个标准差可指出样本均值与μ的可能偏离距离，因此称为均值标准误差

样本N越大，均值标准误差越小

也就是说，样本中的个体越多，样本均值的方差越小，用总体估算样本均值越可靠

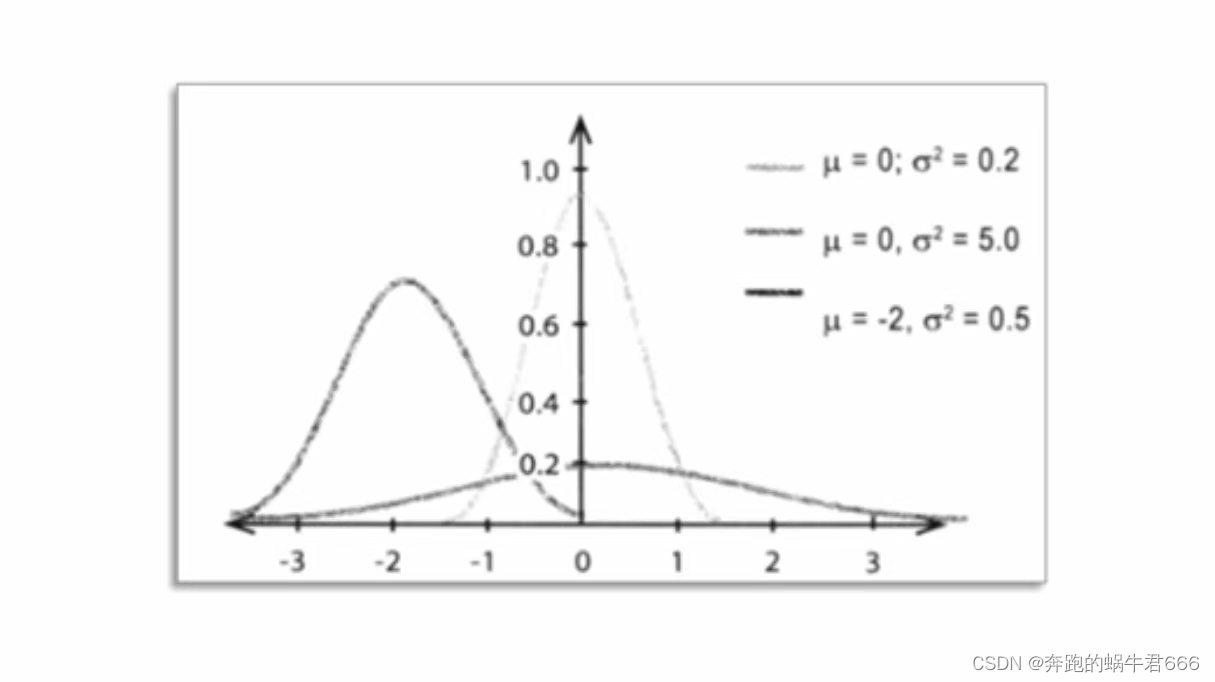
6.中心极限定理

如果X符合正态分布，那么样本均值这个随机变量也符合正态分布

如果X不符合正态分布，但只要N足够大，那样本均值也符合正态分布

在这里，样本均值不是一个数值，而是一个变量，因为从总体中我们可以选出任意多个样本来，每个样本都有一个均值，所以X在这里是一个变量，而是随机变量

7.点估计

利用样本均值得到总体均值的一个具体的估计值

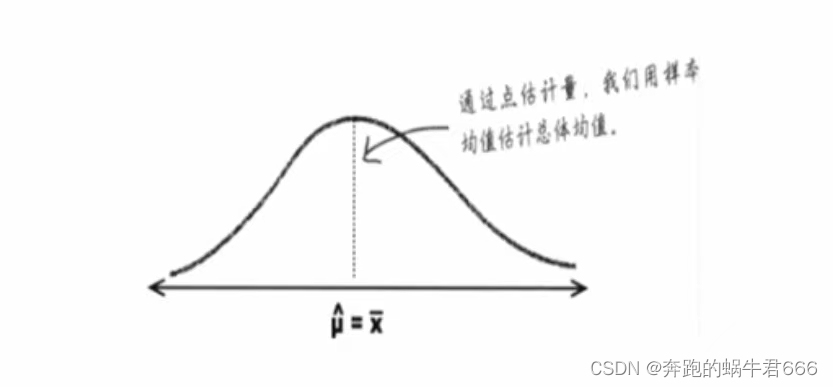
8.区间估计

不要求给出总体均值的精确估计，而是指出总体均值介于数值A和数值B之间，用(A,B)表示这个区间，希望这个区间包含总体均值

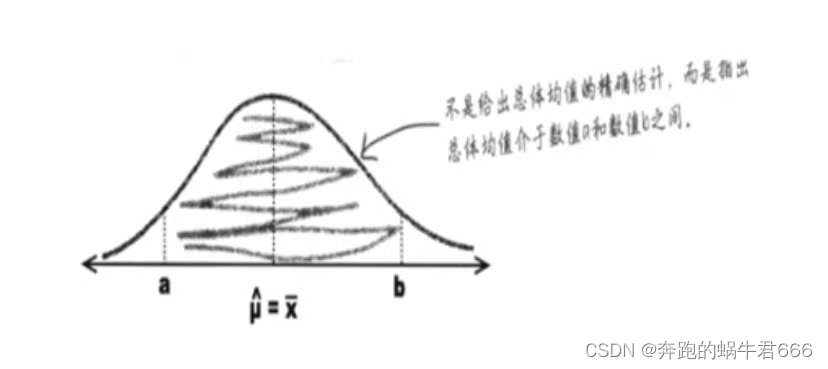
用(A,B)表示区间估计的区间，我们希望这个区间包含总体均值，当然如果区间设置的太大，就没有实际意义了，我们要确定A和B的确切数值，取决于你要设置多大的概率水平，因此，(A,B)被称为置信区间

样本量越大，抽样误差越小，而误差越小，样本的代表性就越好，这时用样本估计总体就越可靠，我们把这种可靠度叫做置信水平，或者置信度

求置信区间的步骤：①求出样本均值 ②计算出抽样误差 ③求出置信区间的两个端点

在样本量相同的情况下，置信水平越高，置信区间越宽

二.假设检验

原理1：小概率事件

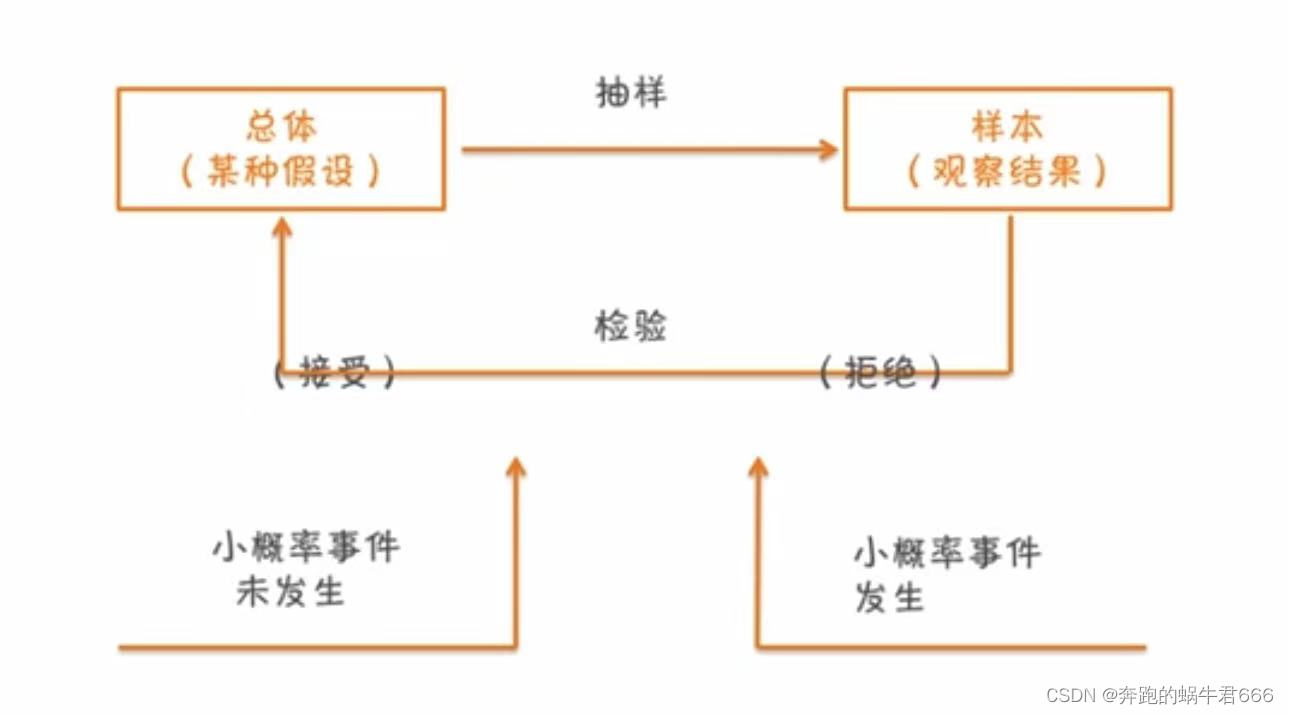
是指小概率事件（p <0.01或 p <0.05）在一次试验中基本上不会发生

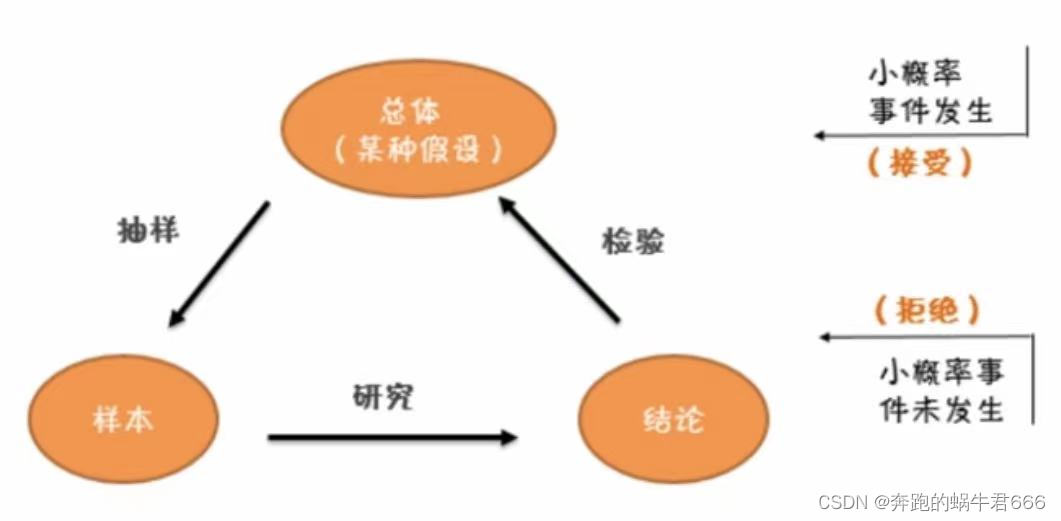
原理2：反证法

先提出某种假设（检验假设H0），再用适当的统计方法确定假设成立的可能性大小，如可能性小，则认为假设不成立

另外，在假设检验里，我们需要先对总体做一个假设，如果我们在对样本的研究中，有95%以上的把握证明原假设是假的，那么就可以否定原假设，在统计学里称为拒绝原假设

1.参数估计和假设检验的联系

假设检验使用的是反证法，可以理解为逆向求解问题

参数估计分为点估计和区间估计，其中区间估计可以理解为正向求解问题

它们两者可以看做同一个问题的不同表述方式

2.显著性水平

在刑事犯罪中，最害怕犯两类错误

第一类错误：把一个无辜的人判为有罪 → 取伪错误

第二类错误：放掉一个有罪的人 → 弃真错误

在假设检验中，我们认为犯第一类错误的后果比犯第二类错误的后果更严重

也就是认为：把一个无辜的人判决为有罪，比放掉一个有罪的人，后果更严重

所以，虽然我们并不能100%保证所有审查公平公正，但我们要尽量把犯“把一个无辜的人判决为有罪”错误的概率控制在一个很小的水平里

我们把这种水平称之为显著性水平α，通常α=0.05

那么，我们最终判了一个人有罪，其实就是说有95%以上的把握判定他犯了罪，同时，有低于5%的可能性误判，即我们保证“把一个无辜的人误判为有罪”的可能性小于5%

在假设检验里，我们需要先对整体做一个假设，如果我们在对样本的研究中，有95%以上的把握证明原假设是假的，那么就可以否定原假设，在统计学里称为拒绝原假设

原假设：要进行检验的断言，除非有足够的证据进行反驳，否则将接受这个断言

备择假设：原假设的对立面（如果原假设成立，备择假设就不成立）

显著性水平：就是拒绝域，用α表示，它表明你希望在观察结果的不可能程度达到多大时决绝H。α越小，为了拒绝原假设，样本结果需要达到的不可能程度越高

P值：是一个拒绝域，它是最小的显著性水平，用它来判断是否拒绝原假设

拒绝域：指的是是否拒绝原假设，假设我们设置的显著性水平也就是拒绝域为0.05，通过计算，如果P值小于0.05，就拒绝原假设；如果大于0.05，说明落在拒绝域之外，就接受原假设

3.步骤

①确定要进行检验的假设

②选择检验统计量 

③确定用于做决策的拒绝域

④求出检验统计量的P值

⑤查看样本结果是否位于拒绝域内

⑥做出决策