实现原理

当遇到需要在题目中寻找一个符合条件的子数组时，或在一段区间内寻找一段连续的区间时，就可以用到这种算法，这个算法的原理就是用左右指针形成一个区间，这个区间用以寻找满足条件的区间

实现思路

具体的实现思路要依托于单调性从而进行同向双指针的优化

这里的单调性并非指的是数据顺序的递增或递减，而是说随着窗口的变大变小或滑动，窗口内数据的整体变化趋势，因此对于一些全为正数的数据量来说，滑动窗口是比较契合解决问题的

那么具体的使用就是定义两个指针，left和right，这两个指针用来作为窗口的左右窗框，这段区间中间的部分就是窗口

既然叫做滑动窗口，那么必然这两个指针是要动起来的，right就是所谓的进窗口，再进行判断是否需要出窗口，再更新结果即可

典型例题

长度最小的子数组

从此题中，其实可以看出滑动窗口是有其大体思路的，简单总结就是进窗口，判断，出窗口，代码形式多样，但核心思路不变，关键在于寻找while循环的条件，也就是出窗口部分的条件是什么

class Solution 
{
public:
    int minSubArrayLen(int target, vector<int>& nums) 
    {
        int left=0,right=0,sum=0,len=INT_MAX;
        for(left=0,right=0;right<nums.size();right++)
        {
            // 进窗口
            sum+=nums[right];

            // 判断
            while(sum>=target)
            {
                // 出窗口
                len=min(len,right-left+1);
                sum-=nums[left];
                left++;
            }

        }
        return len==INT_MAX? 0:len;
    }
};

无重复字符的最小字串

此题的关键思路是找不重复的字串，如果重复就要寻找下一个，那么核心思路不变，依旧是进窗口，判断，出窗口，问题核心关键在于while循环，这里涉及到如果有重复元素在字串中就停止进窗口，因此可以借助一个哈希表来检测是否有重复元素，因此在这里创建一个数组哈希表即可

当检测到元素含有重复元素时，就进行出窗口，出窗口一直出到整个窗口中不含有该重复元素，使得可以继续进窗口找不重复序列

class Solution 
{
public:
    int lengthOfLongestSubstring(string s) 
    {
        int left=0,right=0,hash[128]={0},ret=0;
        for(left=0,right=0;right<s.size();right++)
        {
            // 进窗口
            hash[s[right]]++;
            
            // 判断
            while(hash[s[right]]>1)
            {
                // 出窗口
                hash[s[left++]]--;
            }
            ret=max(ret,right-left+1);
        }
        return ret;
    }
};

最大连续1的个数III

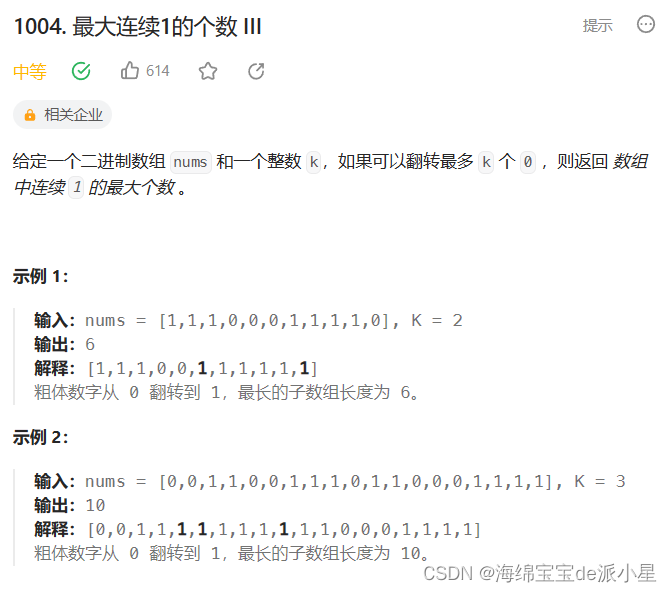
对于此题来说，如果直观去考虑，要按照题意反转数字再进行统计会相当麻烦，因此这里换一种思路进行问题解决

比如，这里可以把题意转换为，使得区间内的0的个数小于K

基于这样的考虑，就可以使用滑动窗口了，整体来看和前面的思维一样，只是需要有一个思维的转换，基于这样的情况下，代码实现并不困难

class Solution 
{
public:
    int longestOnes(vector<int>& nums, int k) 
    {
        int left=0,right=0,len=0,ret=0;
        for(left=0,right=0;right<nums.size();right++)
        {
            // 进窗口
            if(nums[right]==0)
            {
                ret++;
            }

            // 判断
            if(ret>k)
            {
                // 出窗口
                while(nums[left++]!=0);
                ret--;
            }

            len=max(len,right-left+1);
        }
        return len;
    }
};

由此可见，滑动窗口就是三部曲进窗口，判断，出窗口
掌握整个原理即可应对滑动窗口的问题

将x减到0的最小操作

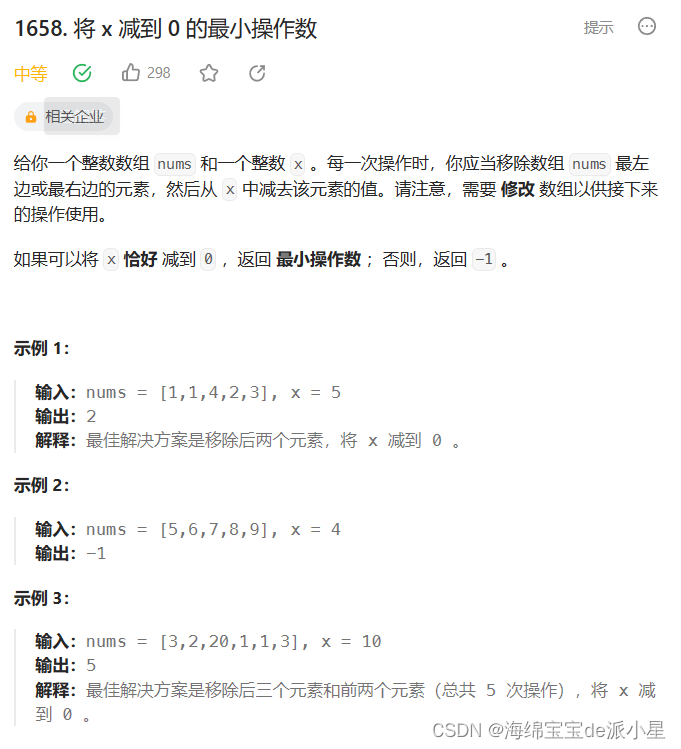
本题用到了一个正难则反的思想，把问题转换为求中间部分的最大值即可，这里要注意对于如果中间没有找到内容要进行记录的问题，并且要一直找下去，要注意更新数据的位置

class Solution 
{
public:
    int minOperations(vector<int>& nums, int x) 
    {
        int sum=0;
        for(int i=0;i<nums.size();i++)
        {
            sum+=nums[i];
        }
        int tmp=sum-x;

        if(tmp<0)
        {
            return -1;
        }

        int left=0,right=0,len=-1,ret=0;
        for(int left=0,right=0; right<nums.size();right++)
        {
            // 进窗口
            ret+=nums[right];

            // 判断
            while(ret>tmp)
            {
                // 出窗口
                ret-=nums[left];
                left++;
            }

            if(ret==tmp)
            {
                len=max(len,right-left+1);
            }
        }
        return len==-1? len:(nums.size()-len);
    }
};

水果成篮

class Solution 
{
public:
    int totalFruit(vector<int>& fruits)
    {
        int hash[100001] = { 0 }, kind = 0, len = 0;
        for (int left = 0, right = 0; right < fruits.size(); right++)
        {
            // 进窗口
            if (hash[fruits[right]] == 0)
            {
                kind++;
            }
            hash[fruits[right]]++;

            // 判断
            while (kind > 2)
            {
                // 出窗口
                hash[fruits[left]]--;
                if (hash[fruits[left]] == 0)
                {
                    kind--;
                }
                left++;
            }

            len = max(len, right - left + 1);
        }
        return len;
    }
};

找到字符串中所有字母异位词(哈希表比较优化)

本题也是滑动窗口的经典题目，和前面不同的是窗口长度是固定的，但整体上遵循进窗口，判断，出窗口的规则就可以解决，但这当中有些许步骤可以优化

先看正常方法如何进行代码编写

class Solution 
{
public:
    bool hashcmp(int a[], int b[], int sz)
    {
        for (int i = 0; i < sz; i++)
        {
            if (a[i] != b[i])
                return false;
        }
        return true;
    }

    vector<int> findAnagrams(string s, string p)
    {
        vector<int> v;
        int hash1[26] = { 0 };
        int hash2[26] = { 0 };
        // p内数据扔到hash1中
        for (auto ch : p)
        {
            hash1[ch - 'a']++;
        }

        for(int left=0,right=0;right<s.size();right++)
        {
            // 进窗口
            char in=s[right];
            hash2[in-'a']++;

            // 判断
            if(right-left+1==p.size())
            {
                if(hashcmp(hash1,hash2,26))
                {
                    v.push_back(left);
                }
                // 出窗口
                char out=s[left];
                hash2[out-'a']--;
                left++;
            }
        }
        return v;
    }
};

这里用数组模拟了两个哈希表，一个哈希表用来存储的是要找的子字符串的数据，另外一个哈希表内存的是滑动窗口内字符串的数据

这里有一个哈希表比较的问题，决定最终能否将left放到vector中的条件就是看这两个哈希表中的元素是否相同，如果相同就可以放到vector中

但比较是个问题，对于这个题来说哈希表中我们只存放了26个字符，比较也只需要比较26次就可以得出结论，但如果这里存放的内容不仅仅是小写字母，还有其他字母？那此时这里再使用每一个元素进行遍历就显得很差，因此这里可以采取一些措施进行相应的优化

对哈希表内元素比较的优化

这个优化方法是采用一个count变量用以表示哈希表中有效字符的个数，假设这里采用的子字符串是abc

那么当入窗口是a的时候，此时哈希表中a的元素对应的数据是0，就可以入数据，此时这个a隶属于有效数据，可以入窗口，但如果要继续入数据a，此时子字符串对应的哈希表中字符a的数据量是1，而滑动窗口中对应的哈希表中字符a对应的数据量已经满足要求了，如果再入该数据则说明这个a是无效的数据，此时count就不进行增加

那么这个有什么用？count进行有效数据的维护和两个哈希表的比较有什么关系？

其实结论在于，在最后判断的时候，如果有效字符的数量和滑动窗口的长度相同，就恰恰说明了滑动窗口对应的哈希表中的数据和子字符串的哈希表中对应的数据是相同的，因此这两个哈希表就是相同的，也就达到了比较哈希表的目的

class Solution 
{
public:

    vector<int> findAnagrams(string s, string p)
    {
        int count=0;
        vector<int> v;
        int hash1[26] = { 0 };
        int hash2[26] = { 0 };
        // p内数据扔到hash1中
        for (auto ch : p)
        {
            hash1[ch - 'a']++;
        }

        for(int left=0,right=0;right<s.size();right++)
        {
            // 进窗口
            char in=s[right];
            hash2[in-'a']++;
            if(hash2[in-'a']<=hash1[in-'a'])
            {
                count++;
            }

            // 判断
            if(right-left+1>p.size())
            {
                // 出窗口
                char out=s[left];
                if(hash2[out-'a']<=hash1[out-'a'])
                {
                    count--;
                }
                hash2[out-'a']--;
                left++;
            }

            if(count==p.size())
            {
                v.push_back(left);
            }
        }
        return v;
    }
};