注意：本文代码为自己理解之后实现，与原论文代码原理相同但并不完全一样，主要是输入张量的形状不同，若更想了解原文代码，可以访问：https://blog.csdn.net/weixin_45084253/article/details/124282580
（加入超链接不太行,)
假设$batchsize$为$1024$，每个元素是一个序列式的特征，比如是一个长为$23$的序列，单个序列元素特征为$708$，则输入进入$ECA$模块的张量形状为$[1024,23,708]$，而$ECA$内部的结构为：

    def call(self, inputs, mask=None):
        nn = tf.keras.layers.GlobalAveragePooling1D()(inputs, mask=mask)
        nn = tf.expand_dims(nn, -1)
        nn = self.conv(nn)
        nn = tf.squeeze(nn, -1)
        nn = tf.nn.sigmoid(nn)
        nn = nn[:,None,:]
        return inputs * nn

首先经过一个全局池化层，则张量$[1024,23,708]$的形状变为$[1024,708]$
$ECA$与普通的$CA$不同的地方在于：
普通的$CA$是对通道先进行降采样，然后进行上采样，而$ECA$作者认为这种做法学不到通道之间的关系，而应该转为学习邻居通道之间的关系，这个是比较有道理，因为我这里面的特征是人脸的$EYE+NOSE+LIP$和手的所有特征，相邻特征之间学习起来更合理，所以作者采用的是一维卷积的方法：

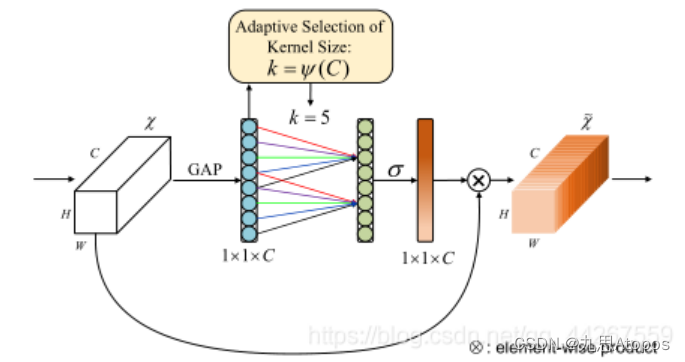
之后由于要进行一维卷积，所以作者对其最后一个维度进行维度扩展:

nn = tf.expand_dims(nn,-1)

也就是张量的形状变成$[1024,708,1]$，经过一维卷积之后：

conv = tf.keras.layers.Conv1D(1,kernel_size=kernel_size,strides=1,padding="same",use_bias=False)

由于这块做了等维的$pad$，所以张量的形状变成了$[1024,708,1]$，注意是对倒数第$2$个进行卷积。到这块其实注意力权重就已经算出来了，接下来需要把最后一维的$1$放到第$2$维上(按照索引来说应该是第$1$维)，也就是：

>>> nn = tf.squeeze(nn,-1)
>>> nn.shape
TensorShape([1024, 708])
>>> nn = nn[:,None,:]
>>> nn.shape
TensorShape([1024, 1, 708])

不要忘记做$sigmoid$操作：

        nn = tf.squeeze(nn, -1)
        nn = tf.nn.sigmoid(nn)
        nn = nn[:,None,:]

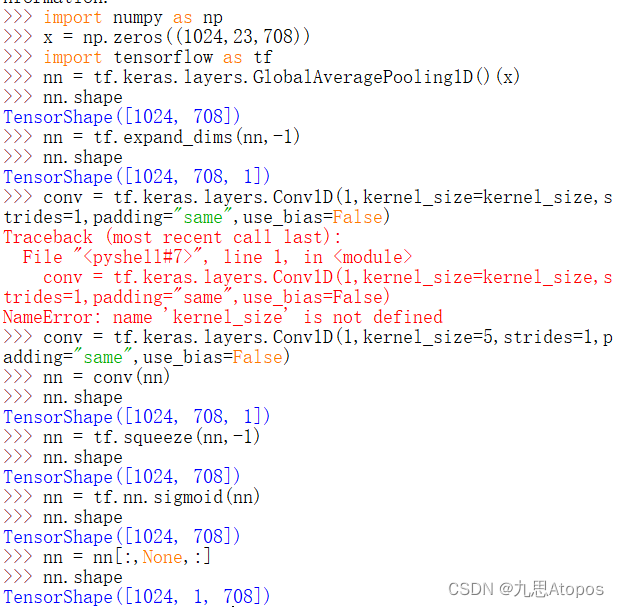
该过程中所有的张量形状的变化为：