文章目录
- B树和B+树
- B树
- B树的定义
- B树的插入操作
- 删除操作
- B+树
- B+树的定义
- B+树的插入操作
- 删除操作
- B树和B+树的区别?
- MySQL数据库为啥用B+树作为索引,而不用B树?
B树和B+树
原文链接:https://blog.csdn.net/jinking01/article/details/115130286
B树
B树的定义
B树也称为B-树,是一颗多路平衡查找树。描述B树的时候需要确定它的阶数,阶数表示一个节点最多可以有几个孩子,一般用m表示。当m=2时,就是二叉搜索树。
对于m阶B树定义如下:
- 每个结点最多有m-1个关键字。
- 根结点可以只有一个关键字。
- 非根节点中至少有Math.ceil(m/2)-1个关键字。
- 每个节点中的关键字都按照从小到大的顺序排列,每个关键字的左子树中的值都小于它,每个右子树的值都大于它。
- 所有叶子节点都位于同一层。

如图是一个4阶B树,每个节点最多个m-1= 3个关键字,非叶子节点至少有Math.ceil(m/2)-1=1个关键字。
B树的插入操作
如果B树中已经存在需要插入的值,则替换掉。如果没有直接添加。
添加步骤如下:
- 根据插入的值找到叶子节点并插入。
- 判断当前节点的个数是否小于等于m-1,满足结束,否则进行下一步
- 以节点中间值(如果是偶数个时选择前一个或者后一个都可以)为中心分裂成左右两个部分,然后将中间值插入到父节点中,插入到父节点后这个中间值左子树指向左半部分,右子树指向右半部分,然后当前节点指向父节点,继续进行第三步。
下面以4阶数为例
先在根节点中插入20、39、91

在插入40:

节点的关键字个数为4大于m-1,按照第三步:我们选择前一个提取。

插入53,21:

插入40:

插入节点关键字个数大于m-1,需要分裂:

插入30,27:

插入33:

插入35:

添加35后分裂得到上图,30插入到父节点后,父节点被称为当前节点,当前节点关键字多了。分裂得到:

删除操作
如果B树中不存在要删除的值则失败。
- 当前需要删除的值在非叶子节点上,则用后续的值替换当前位置。然后在后继节点中删除后继值。此时如果后继节点的关键字个数如果大于等于Math.ceil(m/2)-1,删除结束,否则执行下一步。
- 如果兄弟结点key个数大于Math.ceil(m/2)-1,则父结点中的key下移到该结点,兄弟结点中的一个key上移,删除操作结束。否则,将父结点中的key下移与当前结点及它的兄弟结点中的key合并,形成一个新的结点。原父结点中的key的两个孩子指针就变成了一个孩子指针,指向这个新结点。然后当前结点的指针指向父结点,重复上第2步。
下面以5阶B树为例删除:
原数据如下

删除21:删除21后判断当前节点的关键字个数大于等于Math.ceil(m/2)-1,删除结束。

删除27:27为非叶子节点上的值,所以利用后继记录28替换他。

从图中看出,28替换后原28所在节点的关键字个数小于Math.ceil(m/2)-1。删但是它的兄弟节点有富裕的关键字(也就是兄弟节点关键字个数大于Math.ceil(m/2)-1)。向兄弟节点借一个。所以28下移,26上移。

删除24:在叶子节点直接删除24

发现当前节点关键字个数小于Math.ceil(m/2)-1,此时兄弟节点也只有两个关键字,不能借,只能父节点下沉与两个子节点组成新的节点。

删除40:直接删除后:

同删除24一样,父节点值下沉:

发现父节点的关键字又小于Math.ceil(m/2)-1,父节点的兄弟节点也不能借,父节点的父节点下沉。

B+树
B+树的定义

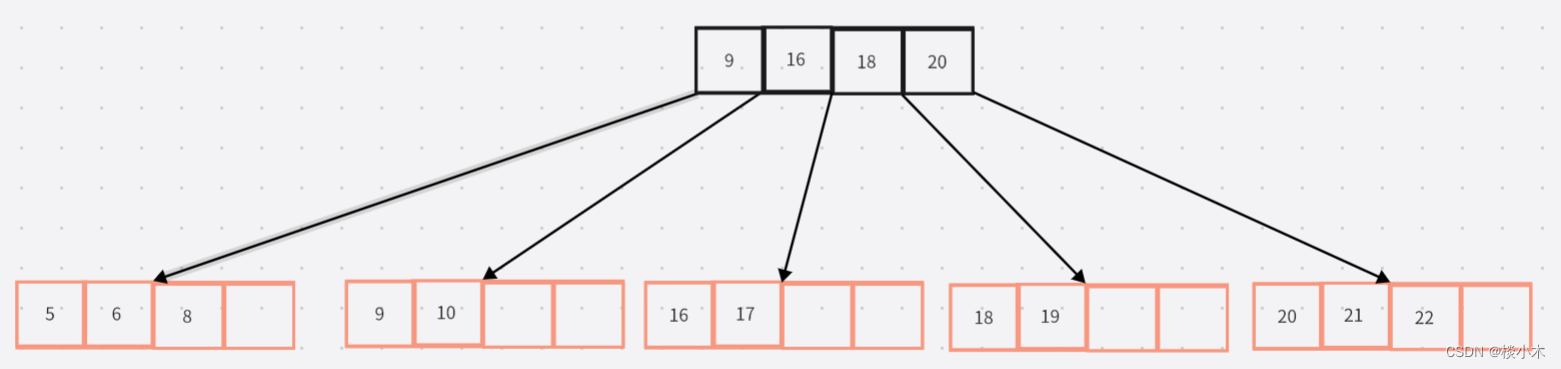
B树和B+树十分类似,B+树的所有叶子节点是链通的(下文中为了画图方便没有体现链接),B+树的关键字个数=最大孩子个数-1;B+树就是将所有数据存储在叶子节点上,非叶子节点只用于索引。上图为4阶B+树,黑色为索引。彩色为叶子节点存储真正的数据。
B+树的插入操作
- 若为空树,创建节点,直接插入值,此时节点也为根节点。
- 针对叶子类型节点:根据值找到待插入的叶子节点位置。插入后判断节点的值的个数是否小于m-1,是则插入结束,不是则将这个叶子节点分裂成两个叶子节点,左叶子节点包含前m/2个记录,右节点包含剩下的记录,将第m/2+1个记录值放进父节点,然后执行下一步。
- 针对索引节点:如果当当前节点记录个数小于等于m-1,插入结束。否则,将这个索引类型节点分裂成两个,左索引节点包含(m-1)/2个记录,右节点树包含m-(m-1)/2个记录,第m/2个节点插入到父节点中。重复第三步。
以5阶B+树为例:
首先依次插入:8,15,5,10:

插入16:在当前节点插入16后:

发现节点的记录值大于m-1,需要将前(m-1)/2作为左子树,第m/2个记录作为父节点的值,m/2及其后面的记录作为右子树。

插入17:

插入18:

调整元素位置:

添加数据直到下图:

现在添加7:节点记录大于m-1

进行分裂:

此时父节点记录个数大于m-1,执行第三步:需要将前(m-1)/2作为左子树,第m/2个记录作为父节点的值,m/2以后的记录作为右子树。

非叶子节点也称为内部节点,表示索引,并且它左子树都小于它,它的右子树都大于它。
删除操作
- 删除叶子结点中对应的值。删除后若结点的值的个数大于等于Math.ceil(m-1)/2 – 1,删除操作结束,否则执行第2步。
- 若兄弟结点值有富余(大于Math.ceil(m-1)/2 – 1),向兄弟结点借一个记录,同时用借到的值替换父结(指当前结点和兄弟结点共同的父结点)点中的值,删除结束。否则执行第3步。
- 若兄弟结点中没有富余的记录,则当前结点和兄弟结点合并成一个新的叶子结点,并删除父结点中的记录(父结点中的这个记录两边的孩子指针就变成了一个指针,正好指向这个新的叶子结点),将当前结点指向父结点(必为索引结点),执行第4步(第4步以后的操作和B树就完全一样了,主要是为了更新索引结点)。
- 若索引结点的记录的个数大于等于Math.ceil(m-1)/2 – 1,则删除操作结束。否则执行第5步
- 若兄弟结点有富余,父结点记录下移,兄弟结点记录上移,删除结束。否则执行第6步
- 当前结点和兄弟结点及父结点下移记录合并成一个新的结点。将当前结点指向父结点,重复第4步。
注意,通过B+树的删除操作后,索引结点中存在的key,不一定在叶子结点中存在对应的记录。也就是在删除时如果叶子结点中没有相应的key,则删除失败。
初始值:

删除22:根据步骤一,删除后节点值个数大于等于Math.ceil(m-1)/2 – 1,删除结束。

删除15:删除后的节点值个数小于Math.ceil(m-1)/2 – 1,执行第二步。

兄弟结点值有富余(大于Math.ceil(m-1)/2 – 1),向兄弟结点借一个记录,同时用借到的值替换父结(指当前结点和兄弟结点共同的父结点)点中的值。可以从兄弟结点借一个关键字为9的记录,同时更新将父结点中的关键字由10也变为9,删除结束。

删除7:删除7之后当前节点只有一个记录,小于Math.ceil(m-1)/2 – 1。而兄弟节点也都不能提供借出,只能将它与一个兄弟节点合并。

执行第四步:合并完成后,父节点记录个数小于Math.ceil(m-1)/2 – 1。兄弟节点也没有多余的记录可以借,那就合并。

执行第六步:
B树和B+树的区别?
B树和B+树主要有两个区别:
- B树的叶子节点和非叶子节点都可以存放键和值,B+树所有数据存储在叶子节点,非叶子节点只存放键。
- B+树的叶子节点是联通的,方便顺序检索。
MySQL数据库为啥用B+树作为索引,而不用B树?
- B+树可以随机查询也可以顺序查询,而B树只能随机查询。
- B+树更加节省空间。B树每个节点都存储键和值,而B+树的内部节点只存储键,这样一个节点就可以存储更多的索引,使得树的高度变低,提高了IO的效率。
- B+树的叶子节点是链接的,可以方便范围查找和顺序查找。
- B+树的性能更加稳定,每次查询都是从根节点到叶子,而B树可能在内部某个节点就已经找到查找到了。
什么时候使用B树合适呢?因为B树在内部节点也会存储值,所以将一些热点访问数据放在距离根节点进的地方,可以提高数据访问效率。综上所说B+树更适合作为索引的结构。