1. 容器适配器

简单的理解容器适配器，其就是将不适用的序列式容器（包括 vector、deque 和 list）变得适用。
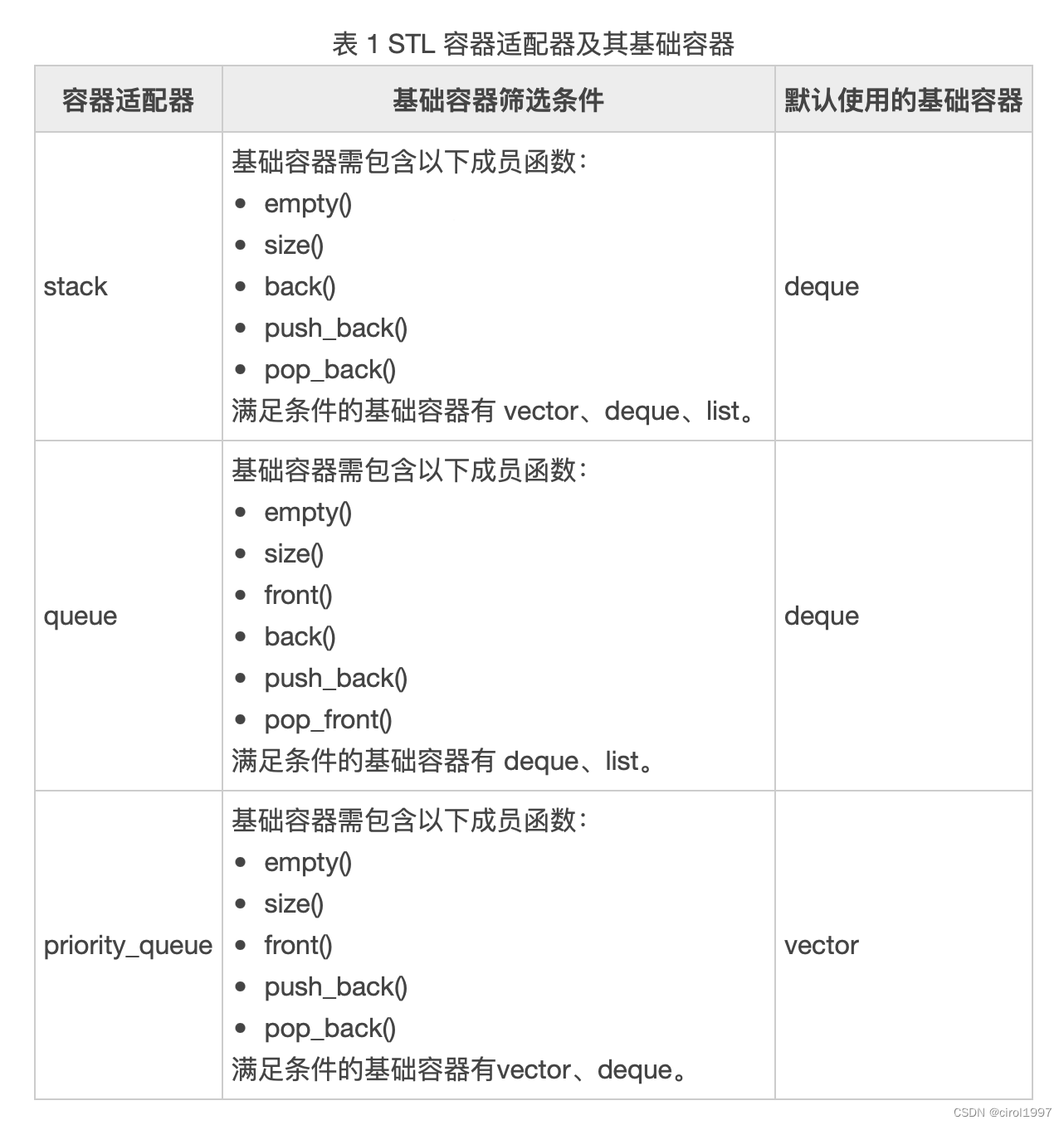
在这里插入图片描述

注意：默认使用的基础容器不代表一定只能用它，比如queue可以用deque，list。

如果你希望你的queue是list那么可以如下创建：

std::queue<int , std::list<int>> q;

可以直接通过 queue 容器适配器来初始化另一个 queue 容器适配器，只要它们存储的元素类型以及底层采用的基础容器类型相同即可。例如：

std::deque<int> values{1,2,3};
std::queue<int> my_queue1(values);
std::queue<int> my_queue(my_queue1);
//或者使用
//std::queue<int> my_queue = my_queue1;

2. priority_queue容器适配器详解

priority_queue 容器适配器模拟的也是队列这种存储结构，即使用此容器适配器存储元素只能“从一端进（称为队尾），从另一端出（称为队头）”，且每次只能访问 priority_queue 中位于队头的元素。
但是，priority_queue 容器适配器中元素的存和取，遵循的并不是 “First in,First out”（先入先出）原则，而是“First in，Largest out”原则。直白的翻译，指的就是先进队列的元素并不一定先出队列，而是优先级最大的元素最先出队列。
priority_queue 容器适配器中存储的元素，优先级是如何评定的呢？很简单，每个 priority_queue 容器适配器在创建时，都制定了一种排序规则。根据此规则，该容器适配器中存储的元素就有了优先级高低之分。
假设当前有一个 priority_queue 容器适配器，其制定的排序规则是按照元素值从大到小进行排序。根据此规则，自然是 priority_queue 中值最大的元素的优先级最高。
priority_queue 容器适配器为了保证每次从队头移除的都是当前优先级最高的元素，每当有新元素进入，它都会根据既定的排序规则找到优先级最高的元素，并将其移动到队列的队头；同样，当 priority_queue 从队头移除出一个元素之后，它也会再找到当前优先级最高的元素，并将其移动到队头。

template <typename T, 
		typename Container=std::vector<T>, 
		typename Compare=std::less<T> >
class priority_queue {
//......
}

可以看到，priority_queue 容器适配器模板类最多可以传入 3 个参数，它们各自的含义如下：

typename T：指定存储元素的具体类型；
typename Container：指定 priority_queue 底层使用的基础容器，默认使用 vector 容器。
typename Compare：指定容器中评定元素优先级所遵循的排序规则，默认使用std::less 按照元素值从大到小进行排序，还可以使用std::greater按照元素值从小到大排序，但更多情况下是使用自定义的排序规则。

作为 priority_queue 容器适配器的底层容器，其必须包含 empty()、size()、front()、push_back()、pop_back() 这几个成员函数，STL 序列式容器中只有 vector 和 deque 容器符合条件。

创建priority_queue

//以使用普通数组或其它容器中指定范围内的数据，对 priority_queue 容器适配器进行初始化：
int values[]{4,1,3,2};
std::priority_queue<int> copy_values(values, values+4); // 4,3,2,1

//使用序列式容器
std::vector<int> vec{1,5,3,4,2}
std::priority_queue<int> pq(vec.begin(), vec.end()); // 5,4,3,2,1

用来初始化的数组或容器中的数据不需要有序，priority_queue 会自动对它们进行排序。

//还可以手动指定 priority_queue 使用的底层容器以及排序规则，比如

std::vector<int> vec{1,5,3,4,2};
std::priority_queue<int, std::vector<int>, std::greater<int>> pq(vec.begin(), vec.end());

注意不支持

std::priority_queue<int, std::vector<int>, std::greater<int>> pq1{2,3,4,1,5};

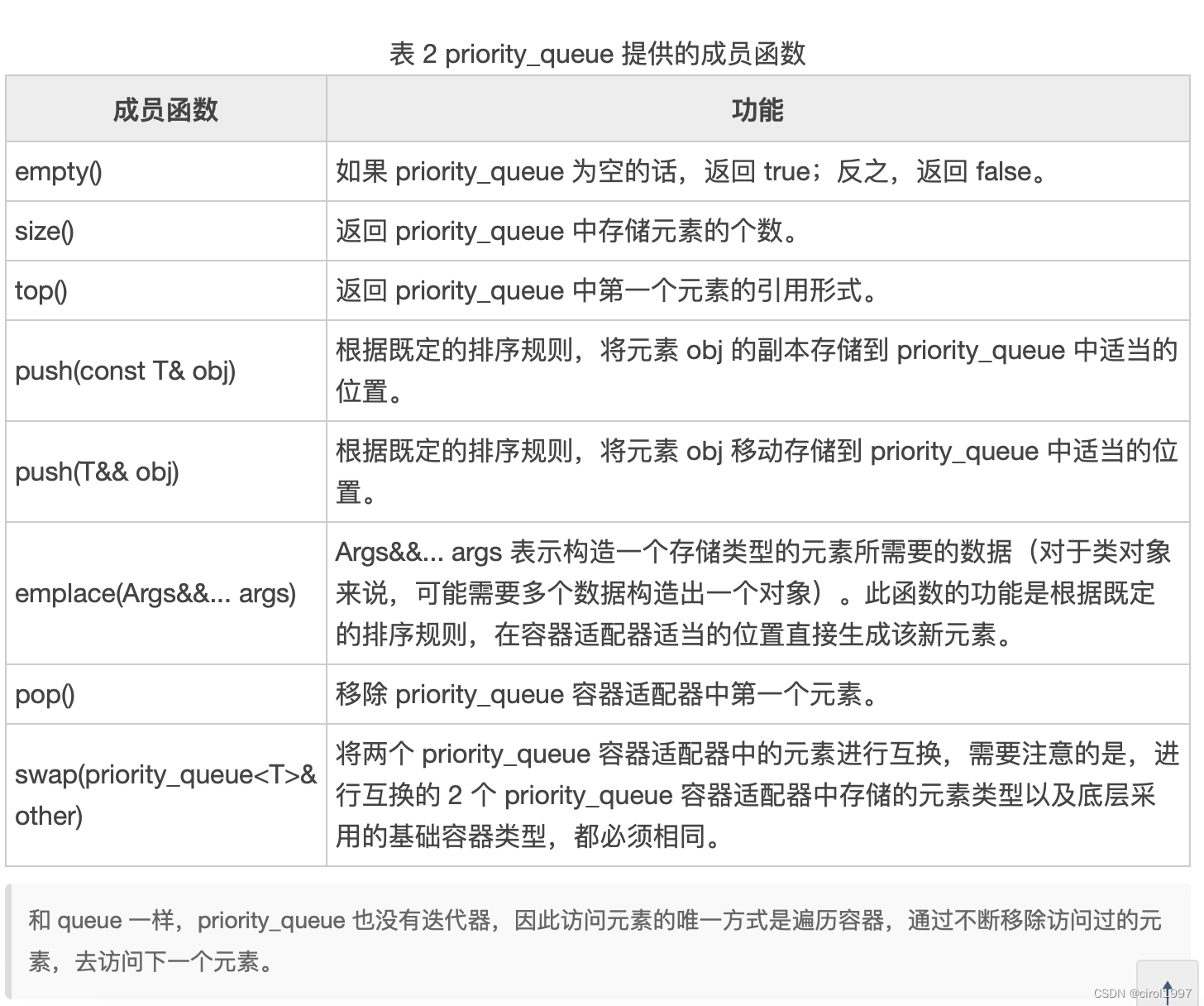
在这里插入图片描述

和 queue 一样，priority_queue 也没有迭代器，因此访问元素的唯一方式是遍历容器，通过不断移除访问过的元素，去访问下一个元素。

    std::vector<int> vec1{1,5,3,4,2};
    std::priority_queue<int, std::vector<int>, std::greater<int>> pq(vec1.begin(), vec1.end());
    while (!pq.empty()) {
        std::cout<< pq.top()<<std::endl;
        pq.pop();
    }
    /*
     1
     2
     3
     4
     5
     */

自定义比较函数-仿函数

greater和less是std实现的两个仿函数（就是使一个类的使用看上去像一个函数，其实现就是类中实现一个operator()，这个类就有了类似函数的行为，就是一个仿函数类了），所以调用的是fun()?

//升序队列
priority_queue <int,vector<int>,greater<int> > q;
//降序队列
priority_queue <int,vector<int>,less<int> >q;

如果自己想模拟less和greater，那么使用的方法应该是这样：

    std::priority_queue<int,std::vector<int>, myFun> pq3(vec1.begin(), vec1.end());
    
    while (!pq3.empty()) {
        std::cout<< pq3.top()<<std::endl;
        pq3.pop();
    }
    /*
     1
     2
     3
     4
     5
     */

自定义比较函数-重载运算符

如果是个自定义类，也可以在自定义类里面自己重载运算符

    std::priority_queue<tmp1> qp2;
    tmp1 t1{2};
    tmp1 t11{3};
    tmp1 t111{1};
    tmp1 t1111{4};
    qp2.push(t1);
    qp2.push(t11);
    qp2.push(t111);
    qp2.push(t1111);
    while (!qp2.empty()) {
        std::cout<< qp2.top().x<<std::endl;
        qp2.pop();
    }
    /*
     5
     4
     3
     2
     1
     */
std::priority_queue<tmp1> qp2;

自定义比较函数-lambda

    auto cmp = [](int a, int b) -> bool { return a < b;};
    std::priority_queue<int, std::vector<int>, decltype(cmp)> pq4(vec1.begin(), vec1.end(),cmp);
    while (!pq4.empty()) {
        std::cout<< pq4.top()<<std::endl;
        pq4.pop();
    }
    /*
     5
     4
     3
     2
     1
     */

补充一个比较有意思的点

前面提到的自定义比较函数-lambda，其实传入的是一个函数指针，什么意思呢？

你可以这样写效果是一样的：

    auto cmp = [](int a, int b)-> bool { return a < b; };
    std::priority_queue<int, std::vector<int>, std::function<bool(int,int)>> pq5(vec1.begin(), vec1.end(),  cmp);
    while (!pq5.empty()) {
        std::cout<< pq5.top()<<std::endl;
        pq5.pop();
    }

但是你不可以这样写：

    std::priority_queue<int, std::vector<int>, decltype(cmp(1,2))> pq4(vec1.begin(), vec1.end(),cmp);
//decltype(cmp(1,2))的到的是bool，而不是函数指针

小问题，好吧，是我理解的不够。

关于priority_queue的底层实现

本来准备单独用一章写，但是看了一下，其实底层实现就是一个堆，特点：

heap是一颗完全二叉树：整颗树除了最底层，都是填满的，而且底层节点从左到右不存在空隙。
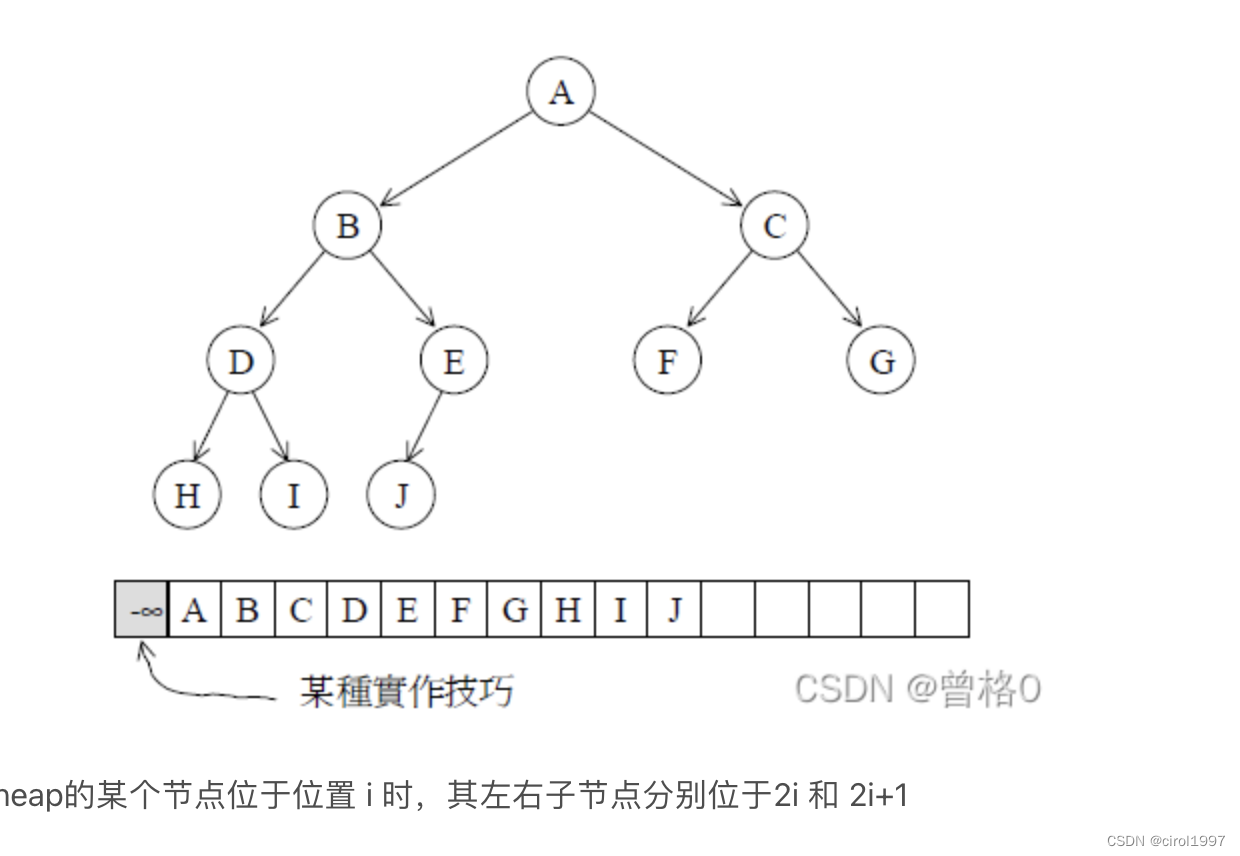
两个操作
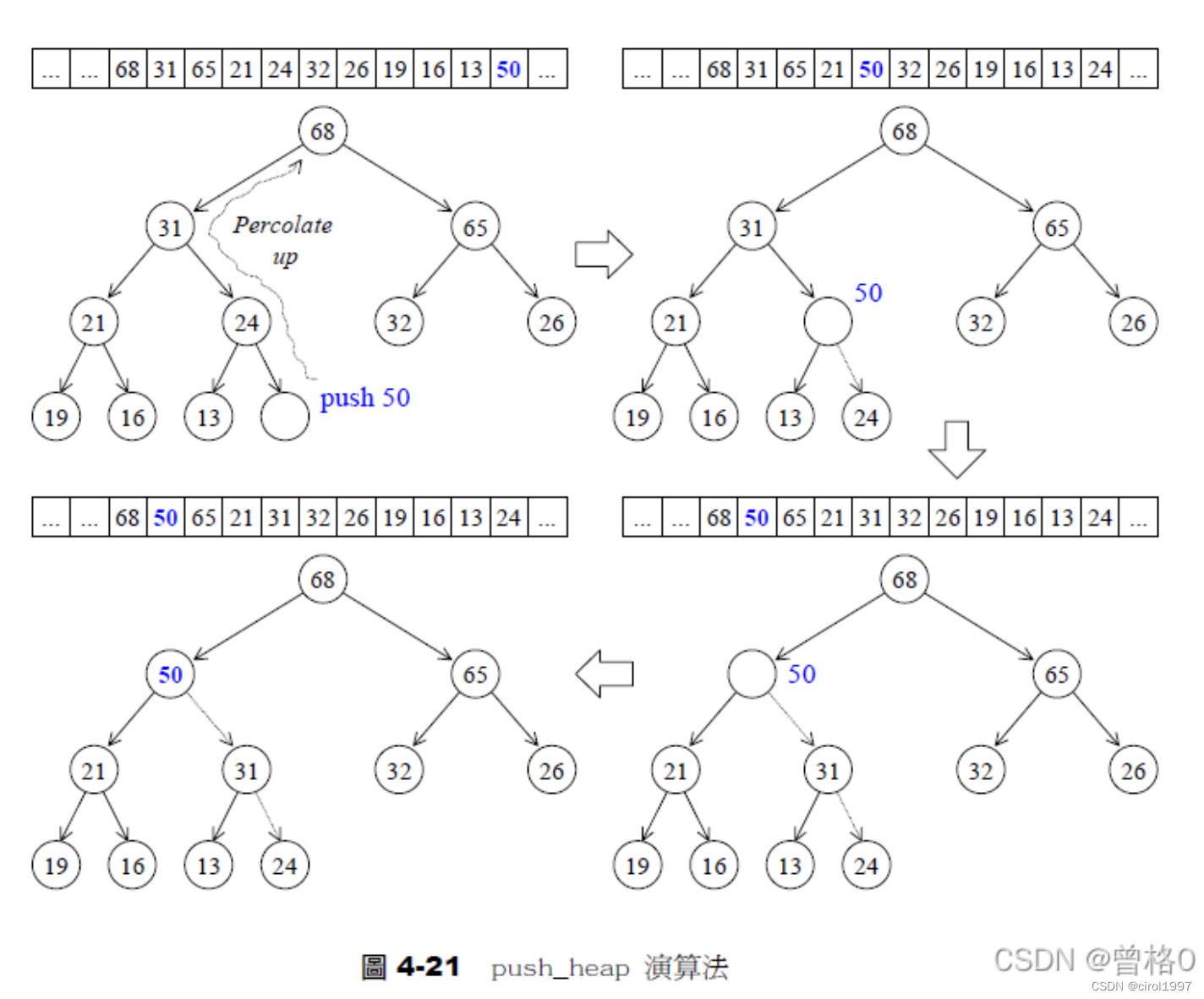
- push_heap：因为要满足完全二叉树的性质，需要将新节点放置在底层节点的最后面，也就是vector的end()，然后执行上溯操作：只要父节点比自己小，就不断调换自己和父节点的位置。
- pop_heap：将heap的最大元素取走，也就是将根节点取走，那根据完全二叉树的性质，得把底层最后面的元素换到根节点。然后不断执行下溯操作：将自己和两个子节点中，较大的那个对调。