【论文解读】Observation-Centric SORT:Rethinking SORT for Robust Multi-Object Tracking

news2024/11/19 13:31:47

一.介绍

1.1 之前卡尔曼方法存在的问题：

1.长时间的运动的线性估计可能是非常不准确的。
2.当没有可用于更新卡尔曼滤波器参数的测量时，标准惯例是信任先验状态估计进行后验更新，这导致了在一段时间内错误的积累。

1.2 基于假设

假设跟踪目标在一定时间间隔内速度恒定，称为线性运动假设。

1.3 SORT的局限性

（1）状态估计噪声的敏感性：尽管高帧率是将物体运动近似为线性的关键，但它也放大了模型对状态估计噪声的敏感性。（噪声和物体的移动是同一量级）

（2）误差随时间的累积：当在KF的更新阶段中没有可用的观测时，通过KF的状态估计的噪声沿着时间累积。

（3）以估计为中心：SORT被设计为通过状态估计而不是观察来延长物体的轨迹。

1.4 本项工作的创新点

（1）设计了一个模块，使用对象状态观察来减少轨迹丢失期间的累积误差。

在传统的预测和更新阶段之外，增加了“重更新”阶段来修正累积误差。重更新是在经过一段时间的未跟踪后，通过与观测相关联而重新激活跟踪时触发的。重更新使用对历史时间步长的虚拟观测来防止错误积累。
虚拟观测来自一个轨迹，该轨迹是由未跟踪前最后一次观测和重新激活该轨迹的最新观测作为锚点生成的。我们将其命名为以观察为中心的重新更新(ORU)。

（2）以为观测中心的动量(OCM)。

将跟踪一致性纳入关联的成本矩阵中

二. OCSort

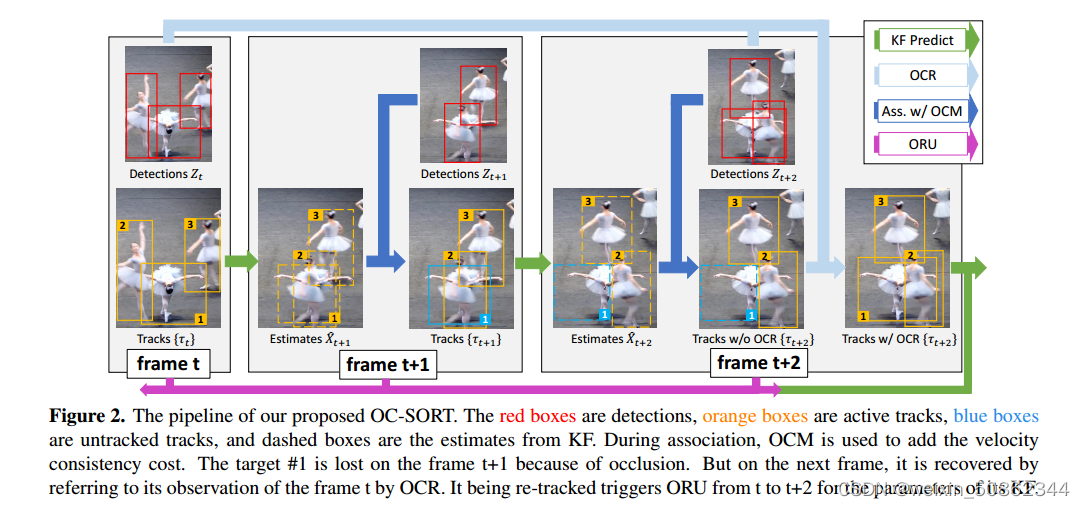
2.1 Observation-centric Re-Update (ORU)

将未跟踪前最后看到的观测值记为 $z_{t1}$ ，将触发重新关联的观测值记为 $z_{t2}$ ，从而构建虚拟轨迹

沿着上述轨迹进行预测-再更新的循环，再更新 的步骤如下：

2.2 Observation-Centric Momentum (OCM)

通过使用观测值去替代估计值，避免了估计值会出现的误差放大问题。

关联的代价矩阵引入状态观测值的一致性项，表述为：

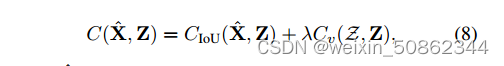
$C_{iou}$ 计算负的两两IoU(Intersection over Union)
$C_v$ 计算①连接现有轨道( $\theta^{track}$ )上的两个观测值和 ②连接轨道的历史观测值和新观测值( $\theta^{intention}$ 方向之间的一致性。
Cv包含所有对 $\Delta \theta = \left | \theta^{track}- \theta^{intention} \right |$ 。在我们的实现中，我们以弧度计算运动方向，即 $\theta =arctan(\frac{v_1 - v_2}{u_1 - u_2})$ ，其中(u1, v1)和(u2, v2)是两个不同时间步长的观测值。

在线性运动模型下，方向估计噪声的尺度与两个观测点之间的时间差呈负相关，即∆t。这表明增加∆t可以实现对θ的低噪声估计。然而，线性运动的假设通常只在∆t足够小时成立。因此，∆t的选择需要权衡。

2.3 heuristic Observation-Centric Recovery (OCR)

OCR将开始第二次尝试将上次观测到的不匹配轨迹与不匹配的观测相关联。

三. 代码

3.1 整体代码架构

整体代码架构类似于bytetrack

3.2 OCM

将运动方向引入了代价矩阵作为关联，即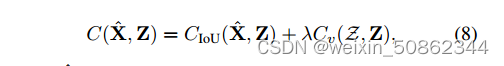

$\Delta \theta = \left | \theta^{track}- \theta^{intention} \right |$ 表示历史运动方向和当前观测的运动方向的弧度的差值

3.2.1 关联函数associate

3.2.1.1 传入参数含义

 #dets：高置信度检测结果
remain_inds = scores > self.det_thresh
dets = dets[remain_inds]
#trks：之前的跟踪轨迹
#iou_threshold：iou匹配阈值
#velocities：之前所有轨迹的跟踪结果
velocities = np.array([trk.velocity if trk.velocity is not None else np.array((0, 0)) for trk in self.trackers])
#k_observations：最新的观测
#k_previous_obs用于返回最新age最大的观测数据
k_observations = np.array([k_previous_obs(trk.observations, trk.age, self.delta_t) for trk in self.trackers])
#inertia：权重
       
matched, unmatched_dets, unmatched_trks = associate(
            dets, trks, self.iou_threshold, velocities, k_observations, self.inertia)

3.2.1.2 associate函数

（代码略有缩减）

（1）angle_diff_cost

Y, X = speed_direction_batch(detections, previous_obs)

def speed_direction_batch(dets, tracks):
    tracks = tracks[..., np.newaxis]
    CX1, CY1 = (dets[:,0] + dets[:,2])/2.0, (dets[:,1]+dets[:,3])/2.0
    CX2, CY2 = (tracks[:,0] + tracks[:,2]) /2.0, (tracks[:,1]+tracks[:,3])/2.0
    dx = CX1 - CX2 
    dy = CY1 - CY2 
    norm = np.sqrt(dx**2 + dy**2) + 1e-6
    dx = dx / norm 
    dy = dy / norm
    return dy, dx # size: num_track x num_det

通过观测数据和轨迹数据获得在x和y方向上像素位置的变化量并对输出数据进行正则化

    inertia_Y, inertia_X = velocities[:,0], velocities[:,1]
    inertia_Y = np.repeat(inertia_Y[:, np.newaxis], Y.shape[1], axis=1)
    inertia_X = np.repeat(inertia_X[:, np.newaxis], X.shape[1], axis=1)

获得速度在x,y方向上的变化量

 diff_angle_cos = inertia_X * X + inertia_Y * Y

$cos(\theta ) =\frac{\vec{a} *\vec{ b}}{\left | \vec{a} \right |*\left | \vec{b} \right |}$ ，传入的inertia_X ， X ， inertia_Y ， Y都是已经正则化的数据

（2）iou_matrix

iou_matrix代价矩阵的计算也不是新东西了

def iou_batch(bboxes1, bboxes2):
    """
    From SORT: Computes IOU between two bboxes in the form [x1,y1,x2,y2]
    """
    bboxes2 = np.expand_dims(bboxes2, 0)
    bboxes1 = np.expand_dims(bboxes1, 1)
    
    xx1 = np.maximum(bboxes1[..., 0], bboxes2[..., 0])
    yy1 = np.maximum(bboxes1[..., 1], bboxes2[..., 1])
    xx2 = np.minimum(bboxes1[..., 2], bboxes2[..., 2])
    yy2 = np.minimum(bboxes1[..., 3], bboxes2[..., 3])
    w = np.maximum(0., xx2 - xx1)
    h = np.maximum(0., yy2 - yy1)
    wh = w * h
    o = wh / ((bboxes1[..., 2] - bboxes1[..., 0]) * (bboxes1[..., 3] - bboxes1[..., 1])                                      
        + (bboxes2[..., 2] - bboxes2[..., 0]) * (bboxes2[..., 3] - bboxes2[..., 1]) - wh)                                              
    return(o)

（3）匹配和对应数据分配

3.3 ORU

3.3.1 关于时间的计算

在OCsort中并没有真正的传入花费的时间，而是通过数据的序号来计算时间

            indices = np.where(np.array(occur)==0)[0]
            index1 = indices[-2]
            index2 = indices[-1]
            time_gap = index2 - index1

3.3.2 生成虚拟路径

3.3.2.1 时间步下的变化

通过未跟踪前最后看到的观测和触发重新关联的观测之间经过的时间步，算出每个时间步下的变化

            time_gap = index2 - index1
            dx = (x2-x1)/time_gap
            dy = (y2-y1)/time_gap 
            dw = (w2-w1)/time_gap 
            dh = (h2-h1)/time_gap

3.3.2.2 恒速运动生成虚拟轨迹

            for i in range(index2 - index1):

                x = x1 + (i+1) * dx 
                y = y1 + (i+1) * dy 
                w = w1 + (i+1) * dw 
                h = h1 + (i+1) * dh
                s = w * h 
                r = w / float(h)
                new_box = np.array([x, y, s, r]).reshape((4, 1))

                self.update(new_box)
                if not i == (index2-index1-1):
                    self.predict()

3.3.2 ORU触发

（1）没有观测数据保存当前卡尔曼参数

        if z is None:
            if self.observed:
                """
                    Got no observation so freeze the current parameters for future
                    potential online smoothing.
                """
                self.freeze()
            self.observed = False 
            self.z = np.array([[None]*self.dim_z]).T
            self.x_post = self.x.copy()
            self.P_post = self.P.copy()
            self.y = zeros((self.dim_z, 1))
            return

（2）重新跟踪到

        if not self.observed:
            """
                Get observation, use online smoothing to re-update parameters
            """
            self.unfreeze()

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/898360.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！