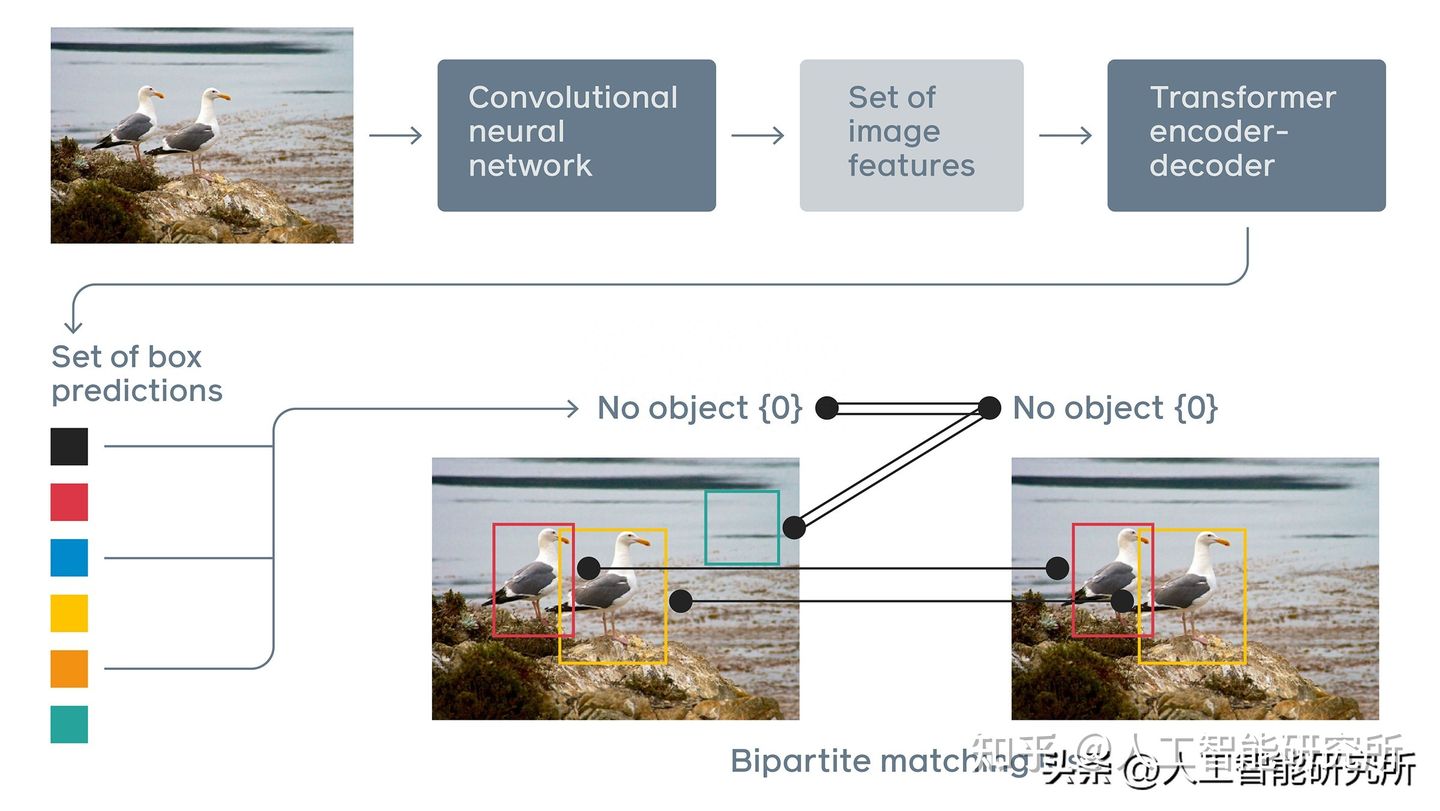
前期的文章我们介绍了DETR模型，我们知道DETR模型首先使用CNN卷积神经网络搜集图片的核心特征点，然后把这些特征点整合起来，通过embedding方法，把特征图片转换到特征向量空间。然后根据标准Transformer模型的编码器与解码器进行注意力机制的计算，最后把计算后的数据进行图片对象的分类，并根据检测到的位置信息，提供对象box区域，方便我们画图。DETR 通过利用标准的Transformer架构来执行传统上特定于对象检测的操作，从而简化了检测管道，优化了算法步骤，提高了检测效率。

但是DETR模型计算效率低，无法有效使用多尺度特征信息。为了解决以上的问题，Focus-DETR利用双重注意力机制重建编码器，且使用了一个跨多尺度特征的自上而下分数调制的前景标记选择器（FTS），大大提高了模型的计算效率。

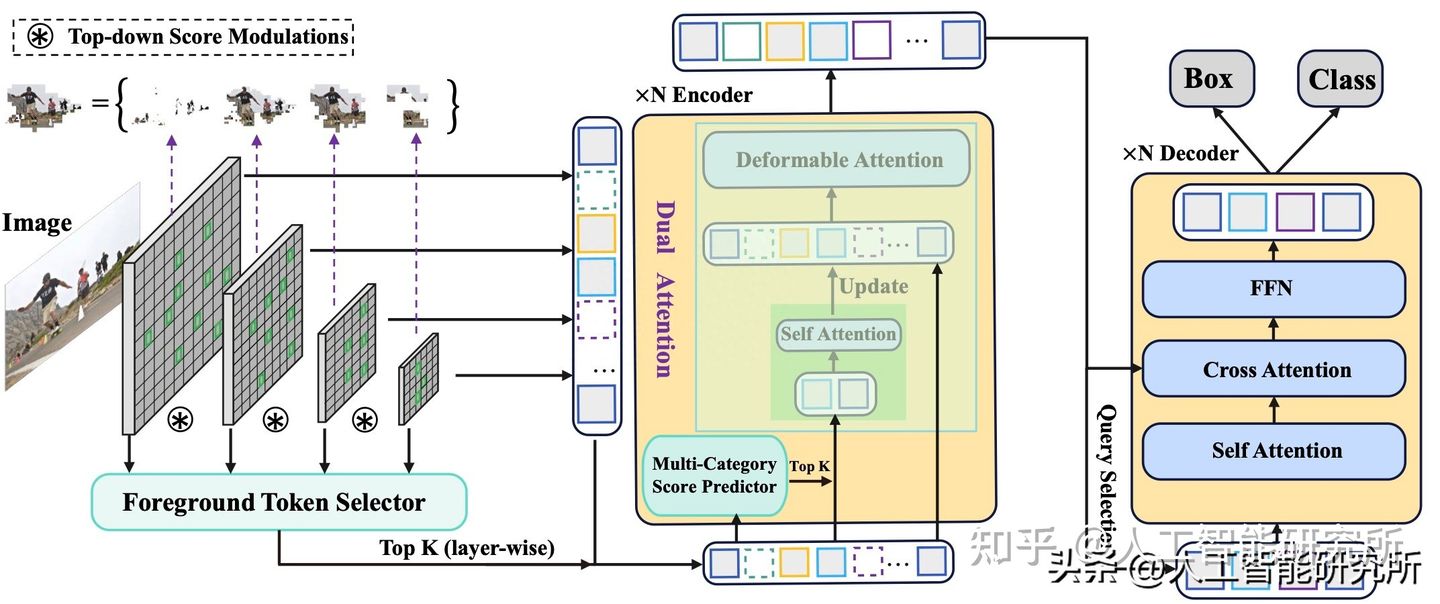
Focus-DETR