这是一道 中等难度 的题

https://leetcode.cn/problems/redundant-connection/

题目

树可以看成是一个连通且 无环 的 无向 图。

给定往一棵 $n$ 个节点 (节点值 $1～n$) 的树中添加一条边后的图。添加的边的两个顶点包含在 $1$ 到 $n$ 中间，且这条附加的边不属于树中已存在的边。图的信息记录于长度为 $n$ 的二维数组 $edges$ ，$edges[i]=[ai,bi]$ 表示图中在 $ai$ 和 $bi$ 之间存在一条边。

请找出一条可以删去的边，删除后可使得剩余部分是一个有着 $n$ 个节点的树。如果有多个答案，则返回数组 $edges$ 中最后出现的那个。

示例 1：

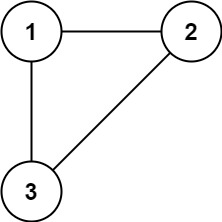
输入: edges = [[1,2], [1,3], [2,3]] 
输出: [2,3] 

示例 2：

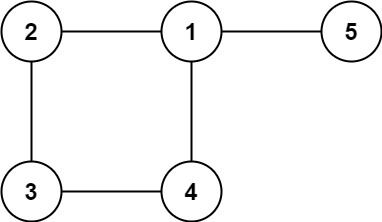
输入: edges = [[1,2], [2,3], [3,4], [1,4], [1,5]] 
输出: [1,4] 

提示:

• $n==edges.length$
• $3<=n<=1000$
• $edges[i].length==2$
• $1<=ai<bi<=edges.length$
• $ai!=bi$
• $edges$ 中无重复元素
• 给定的图是连通的

题解

根据题意，如果把多余的那条边删掉，所有的节点和边会构成一颗树。我们认为这一棵树上的所有节点都是属于同一个集合的。

那么我们可以根据 并查集 的思路，遍历题目给定的二维数组 $edges$，将每次得到的这条边连接的两个点 $x$，$y$ 合并到一个集合当中去。

如果遇到 $x$, $y$ 他两已经在一个集合中了，说明他们之前就已经同在一颗树当中了，也就是说当前这条边就是多余的了，而且由于是按顺序遍历的 $edges$ 数组，也就确保了这条边就是最后出现的。

Java 代码实现

class Solution {
   
    // 存放每个节点所在树的根节点，用于判断是否是同一个集合
    private int[] fa;
    public int[] findRedundantConnection(int[][] edges) {
        int n = edges.length;

        // 舍弃下标为0的位置，从1开始使用
        fa = new int[n + 1];

        // 初始化并查集
        for(int i = 1; i <= n; i++){
            fa[i] = i;
        }

        // 合并集合
        for(int[] edge : edges){
            int x = edge[0];
            int y = edge[1];
            if(find(x) == find(y)){
                // 已经属于同一个集合了
                // 那么当前 edge 就是答案
                return edge;
            }else{
                fa[fa[x]] = fa[y];
            }
        }

        return null;
    }

    private int find(int x){
        if(x == fa[x]){
            return x;
        }
        return fa[x] = find(fa[x]);
    }


}

Go 代码实现

func findRedundantConnection(edges [][]int) []int {

    n := len(edges)

    fa := make([]int, n + 1)

    // 初始化
    for i:=1; i<=n; i++ {
        fa[i] = i
    }

    // 查找集合代表
    var find func(x int) int

    find = func(x int) int {
        if x == fa[x] {
            return x
        }

        fa[x] = find(fa[x])
        return fa[x]
    }

    // 合并集合
    for _, edge := range edges {
        x := edge[0]
        y := edge[1]

        if find(x) == find(y) {
            return edge
        }

        fa[fa[x]] = fa[y]
    }



    return nil
}

复杂度分析

时间复杂度： $O(Nlog(N))$，并查集单次操作的时间复杂度为$O(log(N))$，总计是 $O(Nlog(N))$。

空间复杂度： $O(N)$，主要取决于数组 $fa[]$ 的大小，为 $N+1$。