【算法学习】平方数之和

news2024/9/18 10:37:02

title: 【力扣】633.平方数之和
cover: ‘https://storage.bummon.com/image/202308171051399.png’
tags:

算法
LeetCode
双指针法
二分查找法
categories:
算法笔记
abbrlink: 2911343079
date: 2023-08-17 10:49:52
mathjax: true

【力扣】633.平方数之和

题目

原题链接

给定一个非负整数 c ，你要判断是否存在两个整数 a 和 b，使得 a^2 + b^2 = c 。

示例 1：

输入： c = 5
输出： true
解释： 1 * 1 + 2 * 2 = 5

示例 2：

输入： c = 3
输出： false

提示：

0≤ c ≤ 231-1

双指针法

思路分析

由题意得，我们可以定义两个变量 a 和 b ，使 a * a + b * b = c ，且又可以看到题目中提示了 0≤c ≤231-1 ，那么我们假设a=0，那么b= $\sqrt{c}$ ，此时 a为最小值，b为最大值，那么我们可以得出：

当 a^2 + b^2 == c 时，我们得到了想要的结果
当 a^2 + b^2 > c 时，我们需要让 a 大一些，也就是 a+1
当 a^2 + b^2 < c 时，我们需要让b小一些，也就是 b-1

通过下图来理解。

图解

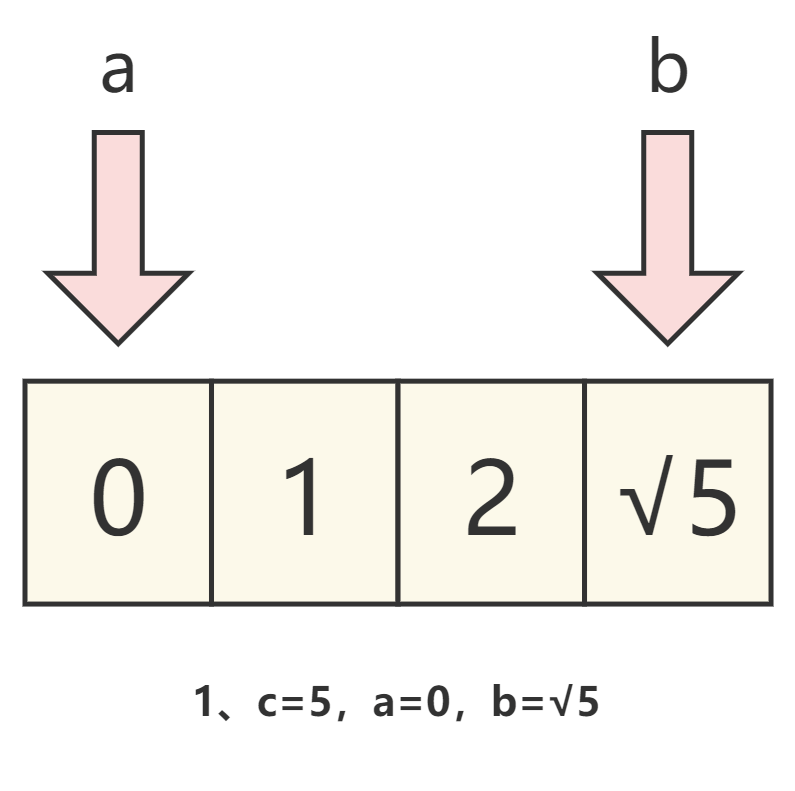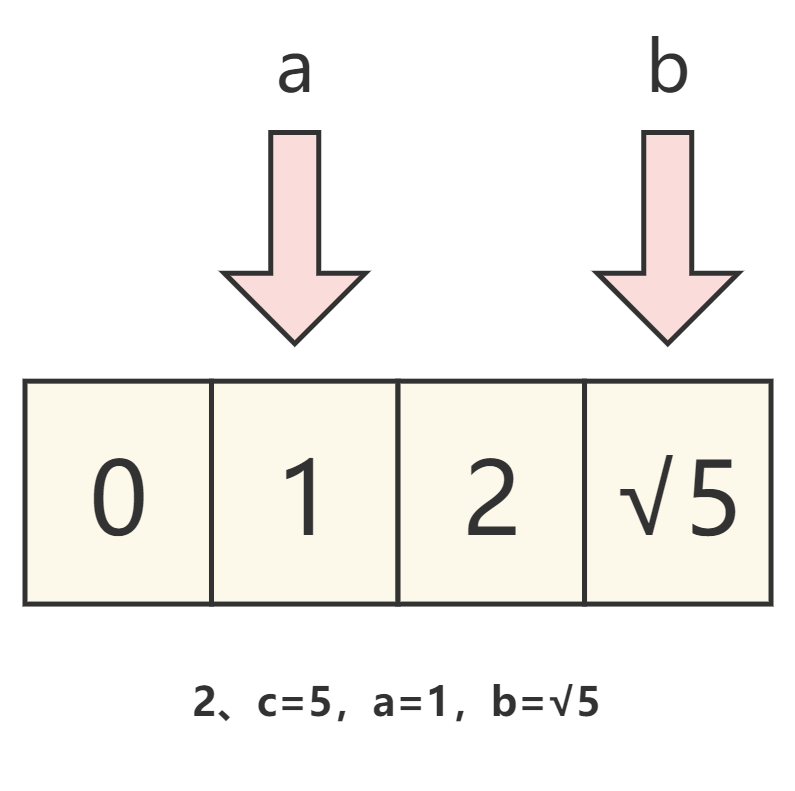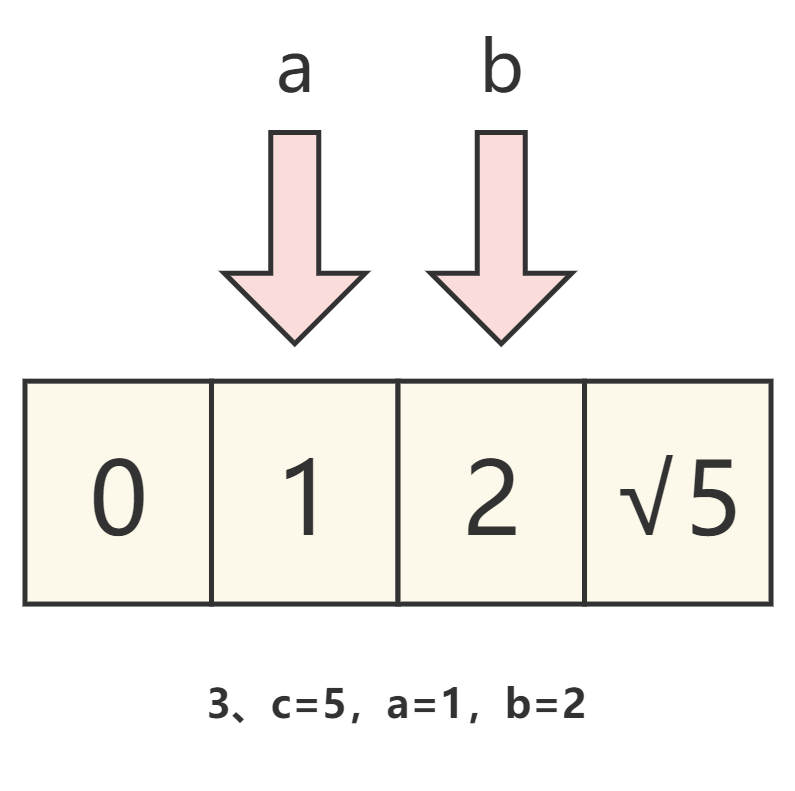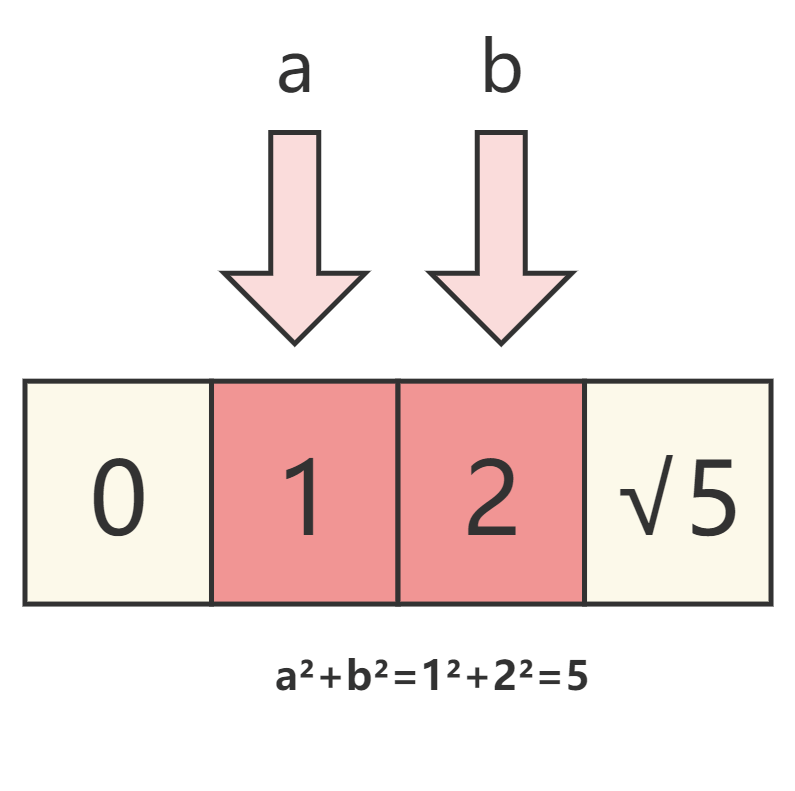
代码实现

public boolean judgeSquareSum(int c) {
    if (c < 0) {
        return false;
    }
    long start = 0;
    long end = (long) Math.sqrt(c);
    while (start <= end) {
        long sum = start * start + end * end;
        if (sum == c) {
            return true;
        } else if (sum > c) {
            end--;
        } else {
            start++;
        }
    }
    return false;
}

sqrt函数法

思路分析

我们还可以使用Java中的 Math.sqrt() 函数来实现，sqrt 函数是一个取根号，我们可以用传入的 c 来减去 a^2，结果设为 b^2 ，最后通过 sqrt 函数来取出 b ，最终我们通过强转 int 来使其变成整数，并判断 强转前的 b 和 强转后的 b 进行对比，如果相等说明取出的 b 为整数，如果不相等那就说明 不是整数，那就继续循环。

代码实现

public boolean judgeSquareSum(int c) {
    for (long a = 0; a * a <=c; a++) {
        double b = Math.sqrt(c - a * a);
        if (b == (int) b) {
            return true;
        }
    }
    return false;
}