分布式系统

基本概念

分布式计算：是利用分布在网络上的各种软、硬计算机资源进行信息处理的过程，它是通过基于网络的分布式系统实现的。

分布式计算的多种形态：

• 网格计算、集群计算；
• 云计算、边缘计算、雾计算；
• 移动计算、普适计算；
• 对等计算。

分布式系统：是使得基于网络互相连接的若干计算单元进行协同计算的软件。对用户而言，好像是面对一个单一的系统。

分布式系统的基本属性：

• 一个分布式系统拥有一定数目的计算单元和一定数目的进程

  • 物理资源：计算单元

  • 逻辑资源：进程

• 进程之间通过消息传递进行通信

• 进程之间以协作的方式交互

• 通信延迟不可忽略

• 任何单个逻辑或物理的资源故障不会导致整个系统的崩溃

• 在资源故障的情况下系统必须具有重新配置和故障恢复的能力

分布式系统的分类：

• 系统设计的角度
  • 时序假设：同步系统、异步系统、部分同步系统
  • 故障假设：随机故障、非随机故障
  • 进程间的通信机制
• 使用规模的角度：个人用户、企业用户、互联网应用
• 基于网络的角度：有线网、无线网；车联网、物联网

分布式算法与集中式算法的区别：

1. 分布式算法是以没有全局时钟为前提的，
2. 没有任何一台机器具有系统的完整状态信息，
3. 每台机器仅根据本地信息进行决策，
4. 一台机器出了故障，不会使整个算法崩溃。

设计目标

1. 连接用户和资源：以一种安全、可靠的方式进行资源共享和用户协作

2. 透明性（Transparency）：

   

   • 100% 的透明性并不总是一个好主意，过分强调透明性可能会带来性能效率上的损失

3. 开放性（Openness）：

   • 它提供的服务的规约应该是完整的和中性的，

     • 完整是指实现所需的所有信息都能在服务的接口中指定，
     • 接口的中性描述是指接口的规约并不规定实现是什么样的，

     完整和中性有助于提高互操作能力和可移植性。

   • 系统应该是灵活的、可扩展 (extensible) 的，

     • 可以把不同开发人员开发的组件搭配起来，配置起来，可以在不影响其它组件的情况下增加、替换组件。

4. 可伸缩性（Scalability）：

   • 在规模上可伸缩 / vertical scalability：可以增加更多的用户和资源，
   • 在地理上可伸缩 / horizontal scalability：用户、资源都可以相距很远，
   • 在管理上可伸缩：能很容易地管理相互独立的组织。

改善系统的可伸缩性：

• 体系结构层面：
  • 对数据、服务进行克隆
  • 对数据、服务、客户进行拆分，分布到不同地点
• 通信层面：
  • 使用异步通信，避免信道拥挤
  • 减少通信
• 容错层面：
  • 隔离故障，避免级联模块的设计，避免单点故障的设计
  • 故障的恢复
• 数据层面：
  • 使用复制、缓存
  • 尽量实现无状态的系统
  • 如果有状态，尽可能在客户端维护会话，或者使用分布式缓存来存放状态

时间

基本概念

秒（second）：铯原子 Cs133 基态的两个超精细能级间跃迁辐射震荡 $9192631770$ 周所持续的时间为 $1$ 秒。

时钟漂移（clock drift）：时钟的绝对偏差，石英钟的漂移率为 $10^{-6}s/s$

时钟偏移（clock skew）：两个时钟在读数上的瞬时差值

UTC（Universal Time Coordinated）：协调世界时，世界标准时间

• 时间的测量：国家授时中心，使用”小铯钟“。

• 时间的发送和接收：长波、短波；网络时间服务器；卫星。

计算机时钟：

1. 硬件时钟：$H(t)$，晶振

2. 软件时钟：$C(t)=\alpha H(t)+\beta$，根据软件调整 $(\alpha ,\beta )$ 的值

3. 分布式系统的每个进程使用各自的本地时间，它们的漂移率各不相同；如果不及时校准，各进程的时钟会偏差很大。

时钟的正确性：设 $t<t^{\prime }$ 是实际时间，$H(t),H(t^{\prime })$ 是相应的硬件时钟值，$\rho >0$ 是漂移率

• 硬件时钟的误差有界性：$(1-\rho )(t^{\prime }-t)\le H(t^{\prime })-H(t)\le (1+\rho )(t^{\prime }-t)$
• 软件时钟的单调性：$t<t^{\prime }\Rightarrow C(t)<C(t^{\prime })$
• 如果计算机时间慢了：在同步点拨快，追上标准时间
• 如果计算机时间快了：不可拨慢（违反单调性），可以调小 $\alpha$ 调大 $\beta$ 使得时钟走的慢一些，等候完美时间

时间同步

外部同步：用权威的外部时间源同步进程的时钟

内部同步：指时钟相互同步

• 内部同步的时钟未必是外部同步的
• 如果系统在范围 $D$ 内是外部同步的，那么同一系统在范围 $2D$ 内是内部同步的

同步系统

1. 已知时钟漂移率的范围
2. 已知最大的消息传输延迟
3. 已知进程每一步的执行时间

有 $2$ 个进程的分布式系统，用 $min$ 表示最小的消息传输延迟，用 $max$ 表示最大的消息传输延迟，

1. 进程 $p$ 发送本地时间 $t$ 给另一个进程 $q$
2. 进程 $q$ 将自己的时钟设置为 $t+(min+max)/2$

与实际时间 $t+T_{trans}$ 相差至多 $(max-min)/2$

有 $N$ 个进程的分布式系统，时间同步算法扩展为：

1. 进程 $p$ 发送当前的本地时间 $t=t_p$ 给其他进程 $q\ne p$
2. 进程 $p$ 等待其他 $N-1$ 个进程的消息，设置 $sum=0$（与自己的时钟偏移）
   1. 收到来自 $q$ 的时间 $t_q$
   2. 计算 $\delta =t_q+(min+max)/2-t_p$（与进程 $q$ 的时钟偏移）
   3. 计算累加值 $sum=sum+\delta$
3. 当前时间为 $t_p^{\prime }$，将自己的时钟设置为 $t_p^{\prime }+sum/N$

系统的 $N$ 个计算机，两两之间的时间差至多为 $\gamma <(max-min)/(1-1/N)$

异步系统

在进程执行时间、消息传递时间和时钟漂移上没有限制的

1. 不知道最大的消息传输延迟，可能是无穷大
2. 但最小的消息传递延迟是可知的

外部同步方法（Cristian 算法）：

1. 使用一个时间服务器 $S$，接收标准时间信号
2. 进程 $p$ 发送给 $S$ 一个请求 $m_r$
3. 服务器 $S$ 回应消息 $m_t$，包含接收到 $m_r$ 的时间 $t$
4. 进程 $p$ 记录发送 $m_r$ 和接收 $m_t$ 之间的往返时间 $T_{round}$
5. 进程 $p$ 设置时钟为 $t+T_{round}/2$

需要 $T_{round}$ 远小于所要求的时间精度，且时间服务器 $S$ 是正确的。由于 $t_e=t_s+T_{round}$ 与 $t$ 的关系为 $t+min<t_e$ 和 $t>t_s+min$，因此 $t_e\in [t+min,t+T_{round}-min]$，精度为 $\pm (T_{round}/2-min)$

内部同步方法（Berkely 算法）：

1. 在计算机集群里挑选一个 Master，其他的作为 Slave
2. Master 周期性地轮询，Slave 将自己的时钟值发送给 Master
3. Master 类似 Cristian 那样观察往返时间，估计 Slave 的本地时间，然后计算所有时间（包括自己）的平均值
4. Master 发送各个 Slave 需要的调整量给对应的 Slave

精确度取决于 Master-Slave 之间的最大往返时间。为了更强的容错：

• Master 使用“容错平均值”（差值在一定范围内的子集），过滤掉异常往返时间
• Master 通过选举产生，这允许 Master 崩溃

网络时间协议（NTP）

NTP（Network Time Protocol）定义了时间服务的体系结构和在 Internet 上发送时间信息的协议。

设计目标：

• 提供一个服务，使得 Internet 上的用户能精确地同标准时间同步：用统计方法来过滤时序数据

• 使得客户能经常有效地重新同步以抵消漂移率：该服务具有对大量客户和服务器的可伸缩性

• 在不可靠的通信链接上提供一个可靠服务：通过提供冗余的服务器以及服务器之间冗余的路径

• 能防止对时间服务的干扰，无论是恶意的还是偶然的：使用认证技术

体系结构：

• 主服务器 (在 root 上) 直接连到外部时间源，例如短波时间接收器、GPS接收器之类的设备。层次 (stratum) $2$ 的服务器与主服务器同步，层次 $3$ 的服务器与层次 $2$ 的服务器同步等等。

• 同步子网是用 Bellman-Ford 路由算法的变种来组织的，构建以主服务器为根的最小权重的支撑树。

故障处理：

• 同步子网可以进行重新配置，以应对服务器不可达或出现故障。

• 如果主服务器的外部时间源出现故障，那么它能变成层次 $2$ 的二级服务器 。

同步方式：

• 组播模式，用于高速LAN环境。一个或多个服务器周期性地将时间组播到其他服务器，并设置它们的时钟 (假设延迟很小)。
• 过程调用模式，类似 Cristian 算法的操作。一个服务器接收来自其他计算机请求，并用时间戳(本地的当前的时钟读数)应答。这个模式适合精确性要求比组播更高的地方，或不能用硬件支持组播的地方。
• 对称模式，用于在LAN中提供时间信息的服务器和同步子网的较高层(较小的层次数)，即要获得最高精确性的地方。一对服务器相互交换有时序信息的消息。

NTP 的消息传递使用 UDP，每个消息携带3个时间戳：

1. 发送前一个 NTP 消息的本地时间
2. 接收前一个 NTP 消息的本地时间
3. 发送当前 NTP 消息的本地时间

服务器 $A$ 发送消息 $m$ 给服务器 $B$，发送时间 $t_{i-3}$（$A$ 的），接收时间 $t_{i-2}$（$B$ 的），传输时间为 $T$

服务器 $B$ 发送消息 $m^{\prime }$ 给服务器 $A$，发送时间 $t_{i-1}$（$B$ 的），接收时间 $t_{i-1}$（$A$ 的），传输时间为 $T^{\prime }$

假设服务器 $A,B$ 的时钟真实偏移为 $o$，估计值为 $o_i$，令 $d_i=T+T^{\prime }$，那么
$$\begin{array}{rl}{t}_{i-2}& =t_{i-3}+t+o\\ t_i& =t_{i-1}+t^{\prime }-o\\ d_i& =(t_{i-2}-t_{i-3})+(t_i-t_{i-1})\end{array}$$
设置估计值 $o_i=(t_{i-2}-t_{i-3}+t_i-t_{i-1})/2$，那么 $o=o_i+(T^{\prime }-T)/2$，得到 $o_i-d_i/2\le o\le o_i+d_i/2$。因此，各个 NTP 服务器之间应该多次执行程序，使用 $d_i$ 最小的 $o_i$ 值作为对 $o$ 的估计。

逻辑时钟 & 向量时钟

发生在先

Lamport 发生在先（happened-before）关系 $\to$，需要满足：

• HB1：如果存在进程 $p_i$ 中的关系 $e{\to }_i{e}^{\prime }$，那么 $e\to e^{\prime }$
• HB2：对于任意的消息 $m$，都有 $send(m)\to receive(m)$
• HB3：如果 $e\to e^{\prime }$ 且 $e^{\prime }\to e^{\prime \prime }$，那么 $e\to e^{\prime \prime }$

发生在先关系的性质：

1. 不能由 $\to$ 排序的两个事件（$e\to e^{\prime }$ 和 $e^{\prime }\to e$ 都不成立），它们是并发事件（可能有资源竞争，不是并行），记做 $e\Vert e^{\prime }$
2. 关系 $\to$ 捕获了以消息传递方式表示的数据流（但不能对非消息传递的数据流动建模）
3. 关系 $\to$ 捕获可能的因果关系，第一个事件不一定会影响第二个事件

逻辑时钟

Lamport 逻辑时钟，是一个单调增长的软件计数器。

每个进程 $p_i$ 维护自己的逻辑时钟 $L_i$，用它给事件打时间戳。事件 $e$，用 $L_i(e)$ 表示 $p_i$ 的时间戳，用 $L(e)$ 表示任意进程中的时间戳。

计算规则：

• LC1：进程 $p_i$ 发出事件 $e$ 之前，首先 $L_i=L_i+1$，然后打戳 $L_i(e)$
• LC2：
  • 发送：进程 $p_i$ 发送消息 $m$ 时，先按照 LC1 打戳，然后在 $m$ 上捎带 $t=L_i$
  • 接收：进程 $p_i$ 接收到 $(m,t)$，先设置 $L_i=\max (L_i,t)$，然后按照 LC1 打戳

逻辑时钟无法区分，是由于局部事件引起的时钟前进，还是由于消息交换引起的时钟前进。

与发生在先的必要不充分关系：

1. 如果 $e\to e^{\prime }$，那么 $L(e)<L(e^{\prime })$
2. 但是 $L(e)<L(e^{\prime })$ 不能推出 $e\to e^{\prime }$

向量时钟

为弥补逻辑时钟的缺点，对于 $N$ 个进程，每个进程 $p_i$ 持有向量 $V_i[1\cdots N]$

1. $V_i[i]$ 是进程 $p_i$ 自己的加时间戳的事件个数（可能与当前事件 $e$ 有发生在先关系的的进程 $p_i$ 上事件个数）
2. $V_i[j],j\ne i$ 是 $p_j$ 中可能会影响 $p_i$ 的事件个数（可能与当前事件 $e$ 有发生在先关系的进程 $p_j$ 上事件个数）

计算规则：

• VC1：初始化 $V_i[j]=0,\forall i,j=1,\cdots ,N$
• VC2：进程 $p_i$ 发出事件 $e$ 之前，首先 $V_i[i]=V_i[i]+1$，然后打戳 $V_i(e)$
• VC3：进程 $p_i$ 发送消息 $m$ 时，先按照 VC2 打戳，然后在 $m$ 上捎带 $t=V_i$
• VC4：进程 $p_i$ 接收到 $(m,t)$，先设置 $V_i[j]=\max (V_i[j],t[j])$，然后按照 VC2 打戳

与发生在先的等价关系：

1. $V=V^{\prime }⟺V[j]=V^{\prime }[j],\forall j=1,\cdots ,N$
2. $V\le V^{\prime }⟺V[j]\le V^{\prime }[j],\forall j=1,\cdots ,N$
3. $V<V^{\prime }⟺(V\le V^{\prime })\wedge (V\ne V^{\prime })$
4. 等价关系：$e\to e^{\prime }⟺V(e)<V(e^{\prime })$
5. 如果 $V(e)<V(e^{\prime })$ 与 $V(e)>V(e^{\prime })$ 都不成立，那么 $e\Vert e^{\prime }$

状态 & 快照

全局状态 & 割集

全局状态：分布式系统可以看作是一系列协同工作的进程集合 $P=P_1，P_2，\dots ，P_n$，进程可以是物理分布的，它们之间通过消息通信实现互操作。分布式系统的全局状态由局部状态集和消息通道状态集组成：

1. 局部状态集，是指系统中的一个进程的全部变量的集合

2. 消息通道状态集，是指在消息传输中的消息序列的集合

观察全局状态的必要性：分布式垃圾回收、分布式调试、死锁判定、程序终止判定、检查点。

一些描述状态的术语：

• 进程的历史：一系列的内部事件、发送事件、接收事件，$history(p_i)=h_i=⟨e_i^0,e_i^1,\cdots ⟩$
• 进程历史的有限前缀：$h_i^k=⟨e_i^0,e_i^1,\cdots ,e_i^k⟩$
• 全局历史：进程历史的并集，$H={\bigcup }_{i=1}^N{h}_i$
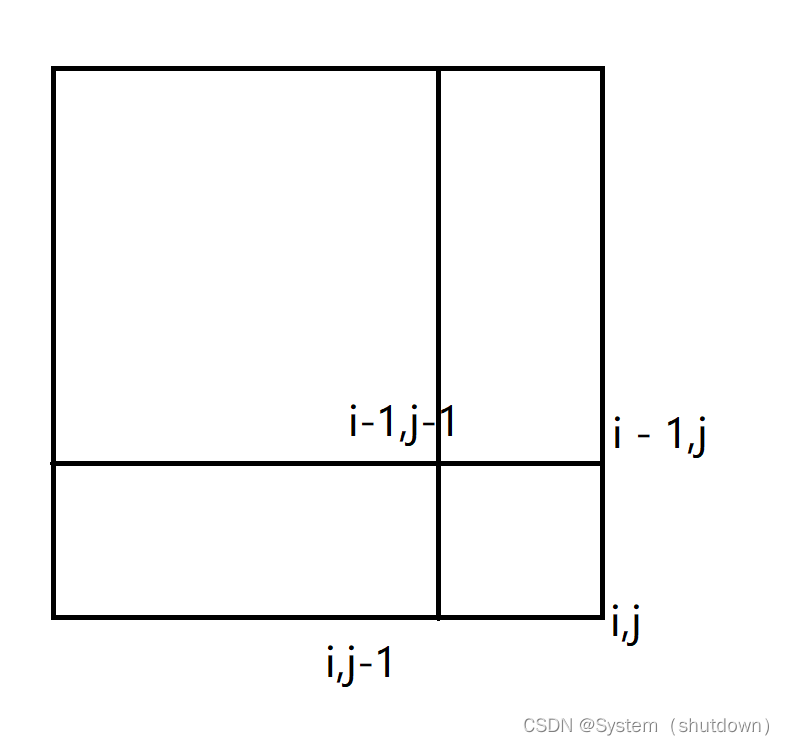
• 割集（Cut）：全局历史的子集，$C={\bigcup }_{i=1}^N{h}_i^{c_i}$
• 割集的边界：进程 $p_i$ 处理的最后一个事件的集合， B = { e i c i } B = \{e_i^{c_i}\} B={eici​​}

一致的割集：它包含的每个事件，它也包含了所有在该事件之前发生的所有事件。如果 $e_i^k\in C$，那么 $\forall e_j^{k^{\prime }}\to e_i^k,e_j^{k^{\prime }}\in C$

一致的全局状态：相对于一致割集的全局状态

快照算法

算法目标：

• 记录进程集的进程状态和通道状态
• 算法所记录的状态组合可能并没有在同一时间发生，但所记录的全局状态是一致的

算法假设：

• 不论是通道还是进程都不出故障
• 通信是可靠的，每个发送的消息最终被完整地接收到恰好一次
• 通道是单向的，提供 FIFO 顺序的消息传递
• 描述进程和通道的图是强连通的 (在任两个进程之间有一条路径)

算法的优点：

• 任一进程可在任一时间开始一个全局快照
• 在照快照时，进程可以继续它们的执行，可以发送和接收正常的消息

Chandy-Lamport Snapshot Algorithm：

1. 标记接收规则：
   1. 进程 $p_i$ 从接收信道 $c$ 上获得标记信息（Marker Message）
   2. 如果 $p_i$ 还没记录自己的进程状态
      1. 记录自己的进程状态
      2. 将接收信道 $c$ 的状态置为空集
      3. 开始记录其他接收信道 $c^{\prime }$ 上的消息
   3. 否则，把接收信道 $c$ 的通道状态记录为 step 1.2.3 的所有接收到的消息集合
2. 标记发送规则：
   1. 进程 $p_i$ 完成了 step 1.2.1 后，
   2. 对每个发送信道 $c$ 上，在发送任何其他消息之前，发送标记信息
3. 算法启动：任一进程 $p_i$ 从一条不存在的接收信道上接收到了一个标记

对算法的理解：

• 在 step 1.2，进程 $p_i$ 启动自己的快照算法。
• 在 step 1.2.2，信道 $c$ 上没有影响当前全局状态的消息了。
• 在 step 1.2.3，除了 $c$ 以外的接收信道上，可能有影响当前全局状态的消息，还没接收到。
• 在 step 2.2，进程 $p_i$ 的每个发送信道上，恰好发送一次标记信息。要么启动对方的快照算法，要么结束对方对这个信道的记录。
• 在 step 1.3，进程 $p_i$ 的每个接收信道上，也恰好只有一次标记信息。当所有接收信道的状态都已被记录，那么终止自己的算法。

最后，这些记录下的状态，可以在各进程本地记录，也可以发送给某个指定进程来收集。